2022-04-02

決定係数（R2）

決定係数（R2）とは

決定係数（ $R^2$ ）とは、回帰分析において用いられる統計的指標の一つで、モデルの適合度を評価するために用いられます。これは、従属変数の変動の何割が独立変数によって説明できるかを示します。 $R^2$ の値は0から1までの範囲で、0は独立変数によって従属変数の変動が全く説明できないことを意味し、1はそれらが全て説明できることを示します。

$R^2$ の式は次のとおりです。

R^2 = 1 - \frac{\sum_{i=1}^{n}(y_i - \hat{y_i})^2}{\sum_{i=1}^{n}(y_i - \bar{y})^2}

ここで、

$y_i$ は、 $i$ 番目のデータポイントにおける従属変数の観測値
$\hat{y_i}$ は、 $i$ 番目のデータポイントにおける従属変数の予測値
$\bar{y}$ は、従属変数の平均値

R2と適合度

適合度は、統計モデルが観測データにどの程度フィットしているかを示す指標です。より高い $R^2$ 値は、モデルがデータに適合していることを示し、従属変数の変動の大部分を説明できることを示します。ただし、高い $R^2$ が独立変数と従属変数の因果関係を意味するわけではなく、 $R^2$ はモデルの性能評価の唯一の基準ではありません。

R2と相関係数

相関係数（ $r$ ）は、2つの変数間の線形関係の強さと方向を示す指標です。相関係数の値は-1（完全な負の相関）から1（完全な正の相関）までの範囲で、0は相関がないことを示します。単回帰分析では、 $R^2$ は相関係数の2乗と等しくなります。つまり、独立変数と従属変数の線形関係によって説明できる従属変数の変動の割合を示します。単回帰分析における $R^2$ の計算式は次のとおりです。

R^2 = r^2

調整済みR2

調整済み $R^2$ は、独立変数の数とサンプルサイズを考慮した $R^2$ の修正版です。複数の回帰分析では、独立変数を追加することによって $R^2$ の値が膨らむことがあり、モデルが実際により良くフィットしているように見えることがあります。調整済み $R^2$ の計算式は次のとおりです。

\text{Adjusted } R^2 = 1 - \frac{(1 - R^2)(n - 1)}{n - k - 1}

ここで、 $n$ はサンプルサイズ、 $k$ は独立変数の数を表します。

調整済み $R^2$ は、従属変数の説明された分散に重要な貢献をしない独立変数を追加することによって、モデルをペナルティーすることによって、過学習を防止し、モデルの選択をサポートします。

Pythonを使用したR2の計算

この章では、Pythonを使用して、カリフォルニア住宅データセットを使用して、 $R^2$ を計算する方法を説明します。

まず、必要なライブラリをインポートし、カリフォルニア住宅データセットを読み込みます。これは、回帰分析に広く使用されている一般的なパブリックデータセットです。

python

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from sklearn.model_selection import train_test_split
from sklearn.datasets import fetch_california_housing

# Load the California Housing dataset
california = fetch_california_housing()
data = pd.DataFrame(california.data, columns=california.feature_names)
data['Price'] = california.target

次に、scikit-learnのLinearRegressionクラスを使用して、線形回帰分析を実行し、r2_score関数を使用して $R^2$ 値を計算します。良い独立変数であるMedIncと悪い独立変数であるHouseAgeを使用して、2つの別々の線形回帰モデルを作成し、両方のモデルの $R^2$ 値を計算します。

python

# Good regression (MedInc vs. Price)
X_good = data[['MedInc']]
y_good = data['Price']

model_good = LinearRegression()
model_good.fit(X_good, y_good)

y_pred_good = model_good.predict(X_good)
r_squared_good = R2_score(y_good, y_pred_good)
print(f'R2 (Good Regression - MedInc vs. Price): {r_squared_good:.2f}')

# Bad regression (HouseAge vs. Price)
X_bad = data[['HouseAge']]
y_bad = data['Price']

model_bad = LinearRegression()
model_bad.fit(X_bad, y_bad)

y_pred_bad = model_bad.predict(X_bad)
r_squared_bad = R2_score(y_bad, y_pred_bad)
print(f'R2 (Bad Regression - HouseAge vs. Price): {r_squared_bad:.2f}')

R2 (Good Regression - MedInc vs. Price): 0.47
R2 (Bad Regression - HouseAge vs. Price): 0.01

期待通り、良い回帰（MedInc vs. Price）の $R^2$ 値が高く、データによりよく適合していることが示されています。一方、悪い回帰（HouseAge vs. Price）の $R^2$ 値は、非常に低く、HouseAge変数がデータに適合していないことを示しています。

最後に、従属変数であるPriceと良い独立変数であるMedInc、そして悪い独立変数であるHouseAgeの間の関係を視覚化します。

python

# Good regression (MedInc vs. Price)
plt.figure(figsize=(10, 6))
sns.regplot(x='MedInc', y='Price', data=data, scatter_kws={'alpha': 0.3}, line_kws={'color': 'red'})
plt.title('Good Regression: MedInc vs. Price')
plt.xlabel('Median Income')
plt.ylabel('Price')
plt.show()

# Bad regression (HouseAge vs. Price)
plt.figure(figsize=(10, 6))
sns.regplot(x='HouseAge', y='Price', data=data, scatter_kws={'alpha': 0.3}, line_kws={'color': 'red'})
plt.title('Bad Regression: HouseAge vs. Price')
plt.xlabel('House Age')
plt.ylabel('Price')
plt.show()

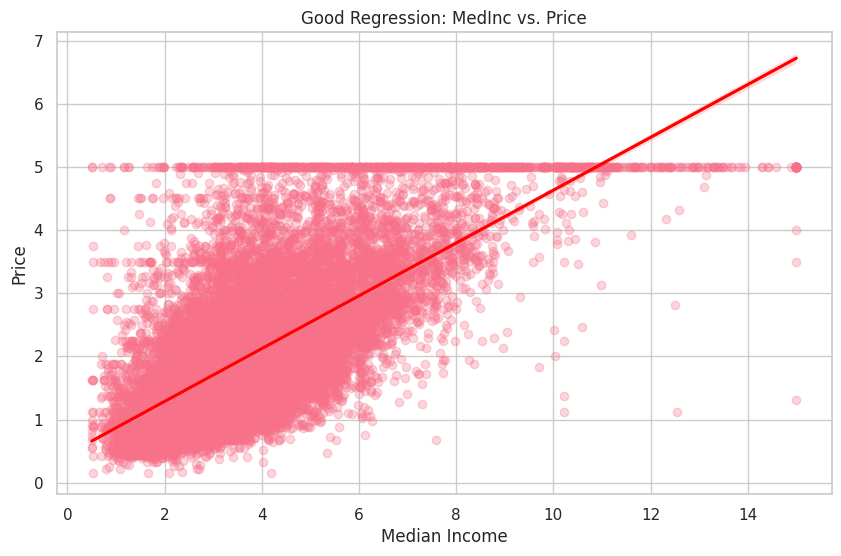
Good fit
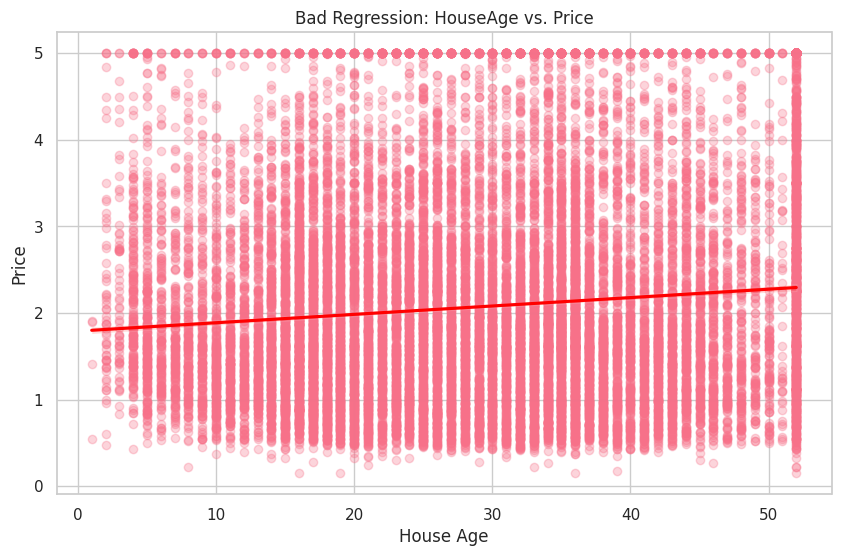
Bad fit

最初のプロットでは、MedIncとPriceの間に明確な正の関係が見られます。一方、2番目のプロットは、HouseAgeとPriceの間の関係が弱いことを示しています。

決定係数（R2）

決定係数（R2）とは

R2と適合度

R2と相関係数

調整済みR2

Pythonを使用したR2の計算

サンプルサイズの決め方

標準正規分布表

Ryusei Kakujo