RNN とは
RNNとは、Recurrent Neural Networkの略で、再帰型ニューラルネットワークとも呼ばれます。RNNは、入力データのシーケンスを処理するためのニューラルネットワークの一種であり、時系列データや自然言語などのような、連続的な入力データを処理するのに適しています。
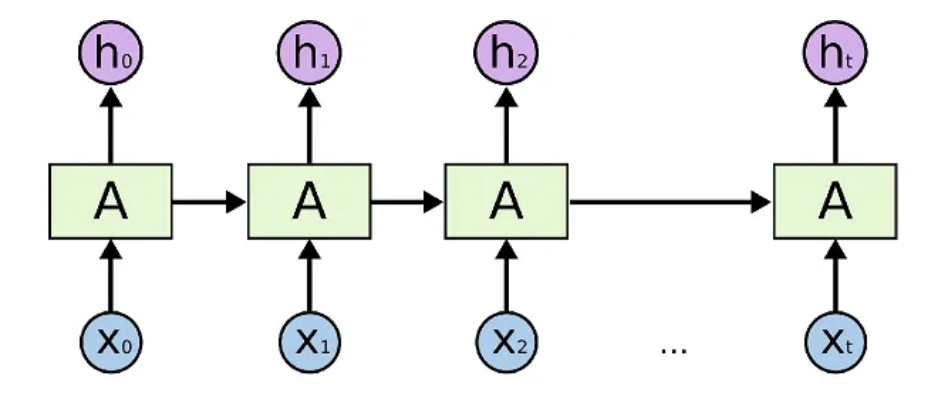
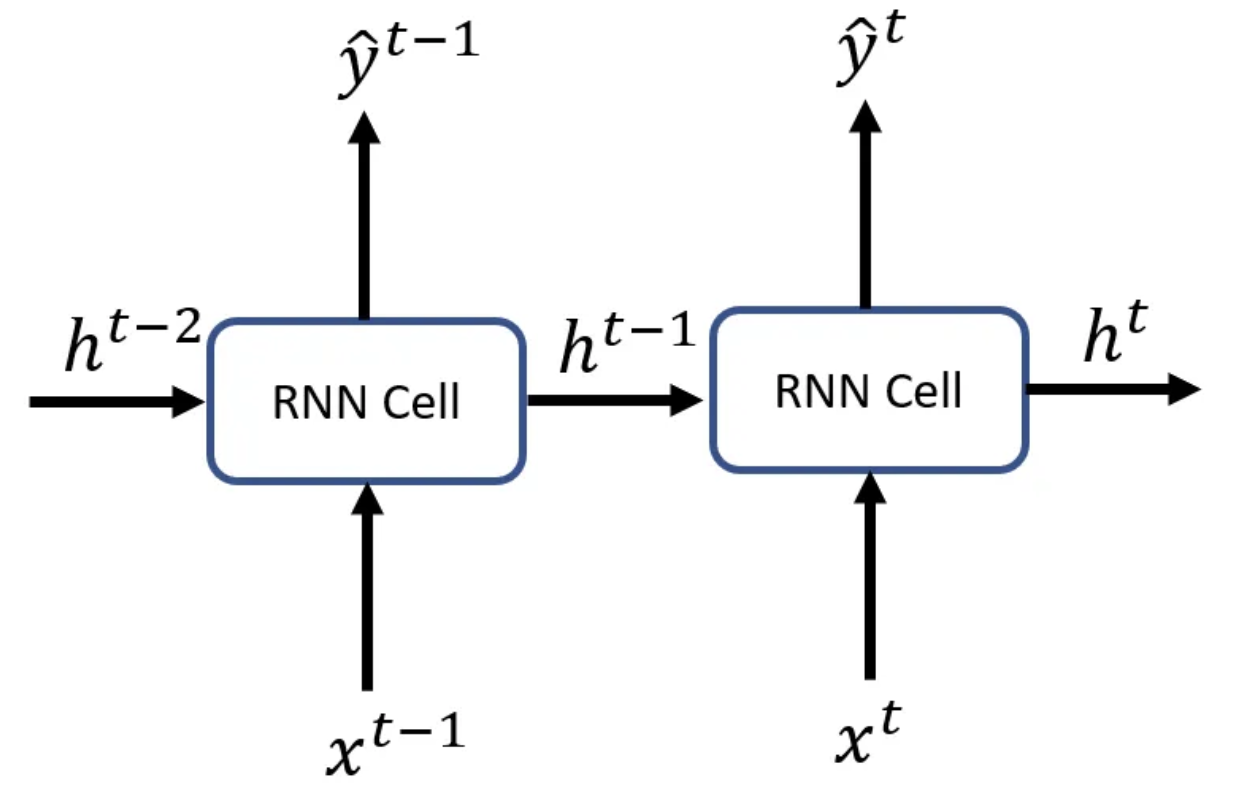
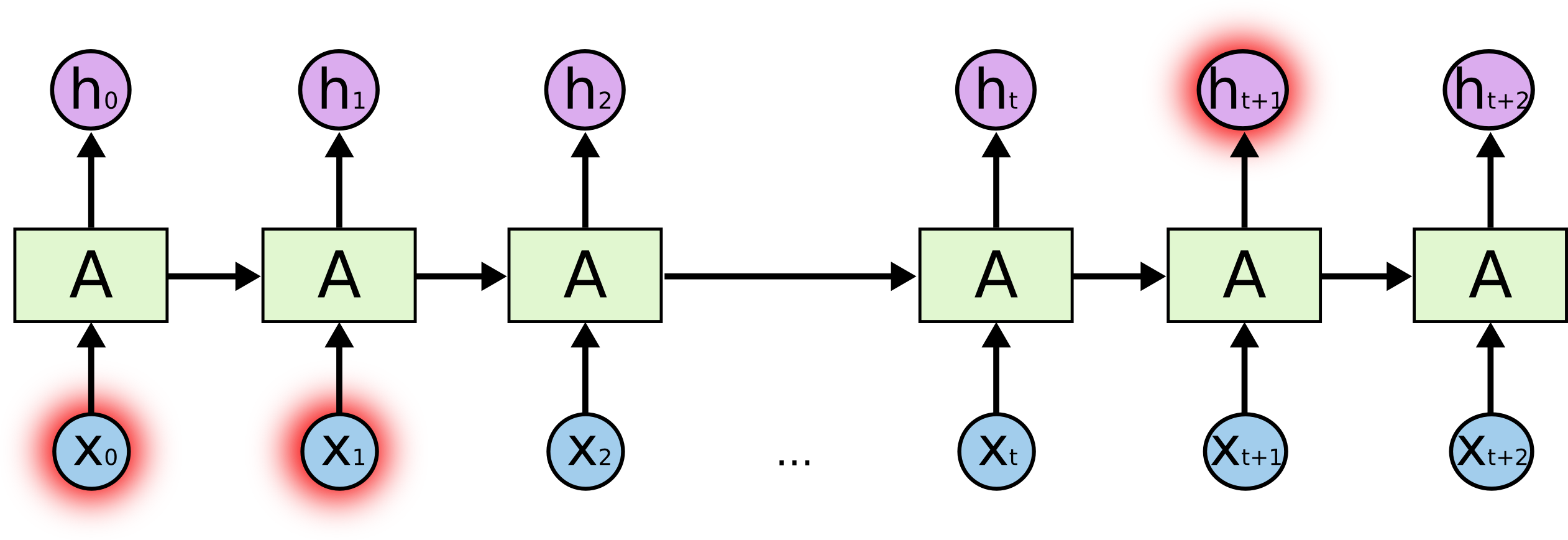
RNNは、時系列データのようなシーケンスを入力とし、それを時間的な依存関係を考慮して処理することができます。RNNは、従来のニューラルネットワークとは異なり、入力に対して状態を保持し、前の状態を次のステップに伝えることができます。これにより、RNNは過去の情報を保持することができます。
次のRNNの図では、時刻
RNNの主なアーキテクチャは、単純なRNN、LSTM、GRUなどがあります。これらのアーキテクチャは、過去の入力データを記憶し、それを現在の入力と組み合わせて出力を生成することができます。これらのアーキテクチャは、時系列データの予測、自然言語処理、音声認識、画像キャプションなどのタスクに使用されます。
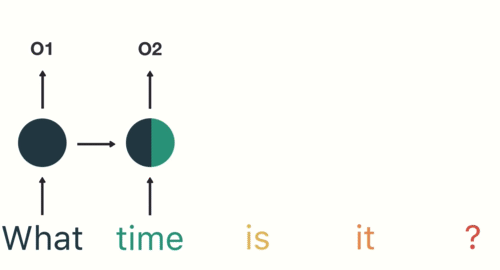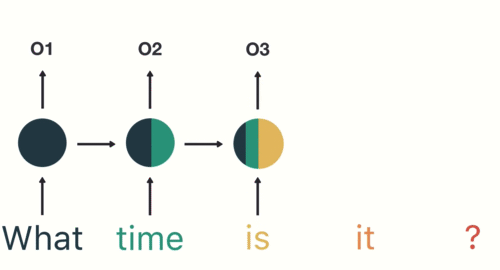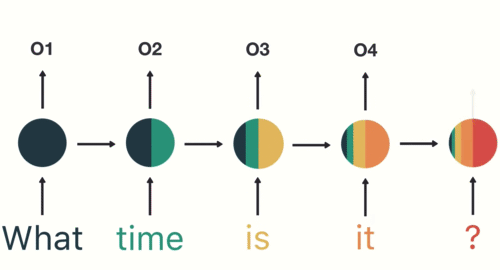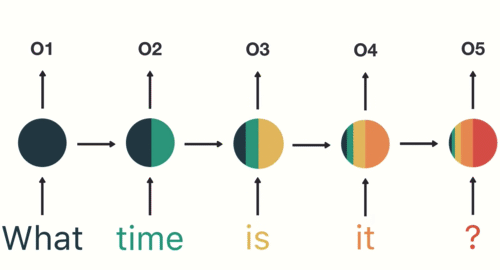
A simple overview of RNN, LSTM and Attention Mechanism
隠れ状態
隠れ状態(hidden state)とは、機械学習や自然言語処理などの分野で使用される用語で、モデルが内部的に保持する、観測されない状態のことを指します。
RNNでは、隠れ状態は過去の入力や自身の出力から計算され、次の入力に関する予測や情報処理に使用されます。入力シーケンスを1つのベクトルに変換し、それを元に隠れ状態を更新します。隠れ状態の存在が、より複雑な問題に対するモデルの表現力を高め、時系列の概念を考慮した予測を可能にします。
あるタイムステップ
隠れ層との違い
隠れ状態(hidden state)と隠れ層(hidden layer)は、深層学習において使用される用語で、似たような概念ですが、少し異なる意味を持ちます。
隠れ状態は、RNNやLSTMなどのモデルで使用される用語で、前の時刻の出力を含めた、内部状態を表します。RNNでは、隠れ状態は次の時刻の入力に影響を与えるため、時系列データの処理に使用されます。LSTMでも同様に、過去の情報を保持するために隠れ状態を使用します。
一方、隠れ層は、多層パーセプトロン(MLP)などのニューラルネットワークで使用される用語で、入力層と出力層の間にある中間層のことを指します。隠れ層は、複数のニューロンから構成され、各ニューロンは前の層からの信号を受け取り、重み付き和を計算し、活性化関数によって出力を生成します。隠れ層が複数存在する場合、それぞれの隠れ層の出力が次の隠れ層や出力層に入力されます。
つまり、隠れ状態と隠れ層は、両方とも機械学習における内部状態を表現する概念ですが、使用される文脈や目的が異なります。隠れ状態は、時系列データの処理に使用され、隠れ層は、一般的なニューラルネットワークの中間層を表します。
RNN の課題
RNNの学習を非常に遅く、非効率的にしている大きな問題が、勾配消失問題です。Feed Forwardニューラルネットワークのプロセスは次のとおりです。
- フォワードパスで何らかの結果を出力する
- その結果を使って損失値を計算する
- その損失値を使って逆伝播を行い、重みに関する勾配を計算する
- 重みに関するこれらの勾配を逆流させて重みを微調整し、ネットワークの性能を改善する
重みの操作は前の層に従って行われるため、小さな勾配は層が変わるごとに大きく減少し、ゼロに非常に近い値になる傾向があるため、初期の層では学習が低下し、全体として効果的な学習ができなくなります。
A simple overview of RNN, LSTM and Attention Mechanism
したがって、勾配が消失すると、RNNはタイムステップに渡る長距離依存性をうまく学習できなくなります。つまり、あるシーケンスの初期の入力が、文脈全体にとって重要であったとしても、その重要度は高くなりません。そのため、長いシーケンスを学習することができず、結果的に短期記憶になってしまいます。
RNN の実装
PyTorchとKerasを使ったRNNの実装例を紹介します。
PyTorch
以下は、PyTorchを使用してRNNモデルを記述する基本的な例です。この例では、シンプルなRNNアーキテクチャを使用して、単語を分類するタスクを実行します。
import torch
import torch.nn as nn
class RNN(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(RNN, self).__init__()
self.hidden_size = hidden_size
self.rnn = nn.RNN(input_size, hidden_size)
self.fc = nn.Linear(hidden_size, output_size)
def forward(self, input):
hidden = torch.zeros(1, 1, self.hidden_size)
output, hidden = self.rnn(input, hidden)
output = self.fc(output[-1, :, :])
return output
このモデルは、input_sizeのサイズの単語を受け取り、hidden_sizeのサイズの隠れ層を持つRNNを通過し、最後にoutput_sizeの数の分類出力を生成します。nn.RNNクラスは、PyTorchに組み込まれているRNNレイヤーであり、nn.Linearは全結合レイヤーを表します。
forwardメソッドは、与えられた入力に対して順伝播を行います。最初に、隠れ層を初期化します。次に、入力と現在の隠れ層をRNNに渡し、出力と新しい隠れ層を取得します。最後に、出力の最後のステップのみを取得し、全結合レイヤーを介して分類出力を生成します。
他にも次のような実装例があります。
Keras
KerasでRNNを実装します。
まずはRNNに用いる訓練データを作成します。サイン関数に乱数でノイズを加えたデータを作成します。
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
x_data = np.linspace(-2*np.pi, 2*np.pi) # -2π to 2π
sin_data = np.sin(x_data) + 0.1*np.random.randn(len(x_data)) # add noise to sin func
plt.style.use('ggplot')
plt.figure(figsize=(12, 8))
plt.plot(x_data, sin_data)
plt.show()
n_rnn = 10 # num of time series
n_sample = len(x_data)-n_rnn # num of samples
x = np.zeros((n_sample, n_rnn)) # input
t = np.zeros((n_sample, n_rnn)) # label
for i in range(0, n_sample):
x[i] = sin_data[i:i+n_rnn]
t[i] = sin_data[i+1:i+n_rnn+1]
x = x.reshape(n_sample, n_rnn, 1)
t = t.reshape(n_sample, n_rnn, 1)
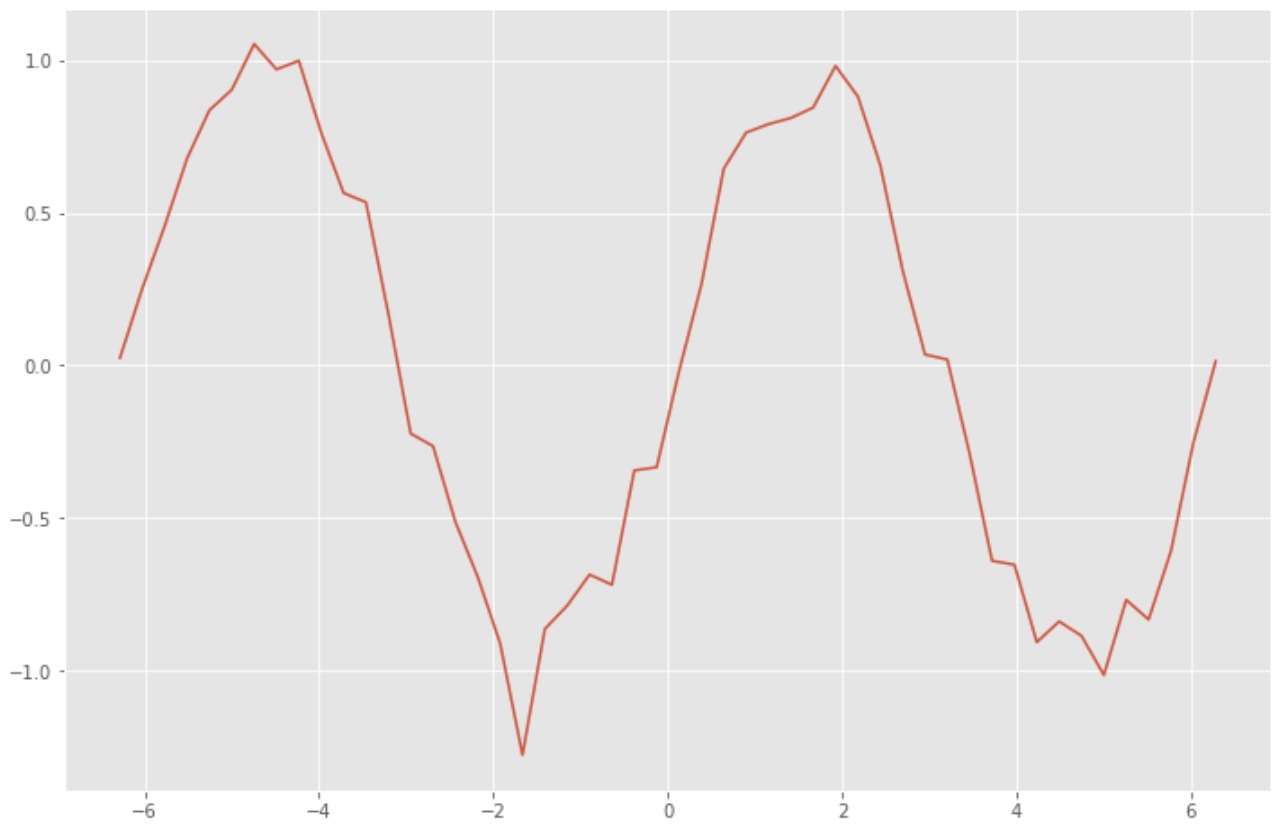
過去の時系列データから未来の値を予測するRNNモデルを構築します。
from keras.models import Sequential
from keras.layers import Dense, SimpleRNN
batch_size = 8 # batch size
n_in = 1 # num of neurons in input layer
n_mid = 20 # num of neurons in mid layer
n_out = 1 # num of neurons in output layer
model = Sequential()
model.add(SimpleRNN(n_mid, input_shape=(n_rnn, n_in), return_sequences=True))
model.add(Dense(n_out, activation="linear"))
model.compile(loss="mean_squared_error", optimizer="sgd")
print(model.summary())
>> Model: "sequential"
>> _________________________________________________________________
>> Layer (type) Output Shape Param #
>> =================================================================
>> simple_rnn (SimpleRNN) (None, 10, 20) 440
>>
>> dense (Dense) (None, 10, 1) 21
>>
>> =================================================================
>> Total params: 461
>> Trainable params: 461
>> Non-trainable params: 0
>> _________________________________________________________________
>> None
構築したRNNのモデルを使って学習を行います。
history = model.fit(x, t, epochs=20, batch_size=batch_size, validation_split=0.1)
>> Epoch 1/20
>> 5/5 [==============================] - 2s 79ms/step - loss: 0.6561 - val_loss: 0.3590
>> Epoch 2/20
>> 5/5 [==============================] - 0s 13ms/step - loss: 0.4701 - val_loss: 0.2707
>> Epoch 3/20
>> 5/5 [==============================] - 0s 11ms/step - loss: 0.3694 - val_loss: 0.2240
>> Epoch 4/20
>> 5/5 [==============================] - 0s 11ms/step - loss: 0.3051 - val_loss: 0.1892
>> Epoch 5/20
>> 5/5 [==============================] - 0s 15ms/step - loss: 0.2613 - val_loss: 0.1696
>> Epoch 6/20
>> 5/5 [==============================] - 0s 13ms/step - loss: 0.2289 - val_loss: 0.1593
>> Epoch 7/20
>> 5/5 [==============================] - 0s 12ms/step - loss: 0.2058 - val_loss: 0.1501
>> Epoch 8/20
>> 5/5 [==============================] - 0s 12ms/step - loss: 0.1889 - val_loss: 0.1414
>> Epoch 9/20
>> 5/5 [==============================] - 0s 13ms/step - loss: 0.1750 - val_loss: 0.1345
>> Epoch 10/20
>> 5/5 [==============================] - 0s 14ms/step - loss: 0.1633 - val_loss: 0.1274
>> Epoch 11/20
>> 5/5 [==============================] - 0s 12ms/step - loss: 0.1540 - val_loss: 0.1233
>> Epoch 12/20
>> 5/5 [==============================] - 0s 12ms/step - loss: 0.1456 - val_loss: 0.1188
>> Epoch 13/20
>> 5/5 [==============================] - 0s 11ms/step - loss: 0.1377 - val_loss: 0.1133
>> Epoch 14/20
>> 5/5 [==============================] - 0s 12ms/step - loss: 0.1317 - val_loss: 0.1097
>> Epoch 15/20
>> 5/5 [==============================] - 0s 11ms/step - loss: 0.1256 - val_loss: 0.1063
>> Epoch 16/20
>> 5/5 [==============================] - 0s 11ms/step - loss: 0.1199 - val_loss: 0.1025
>> Epoch 17/20
>> 5/5 [==============================] - 0s 13ms/step - loss: 0.1152 - val_loss: 0.1025
>> Epoch 18/20
>> 5/5 [==============================] - 0s 11ms/step - loss: 0.1105 - val_loss: 0.0958
>> Epoch 19/20
>> 5/5 [==============================] - 0s 11ms/step - loss: 0.1065 - val_loss: 0.0932
>> Epoch 20/20
>> 5/5 [==============================] - 0s 15ms/step - loss: 0.1025 - val_loss: 0.0897
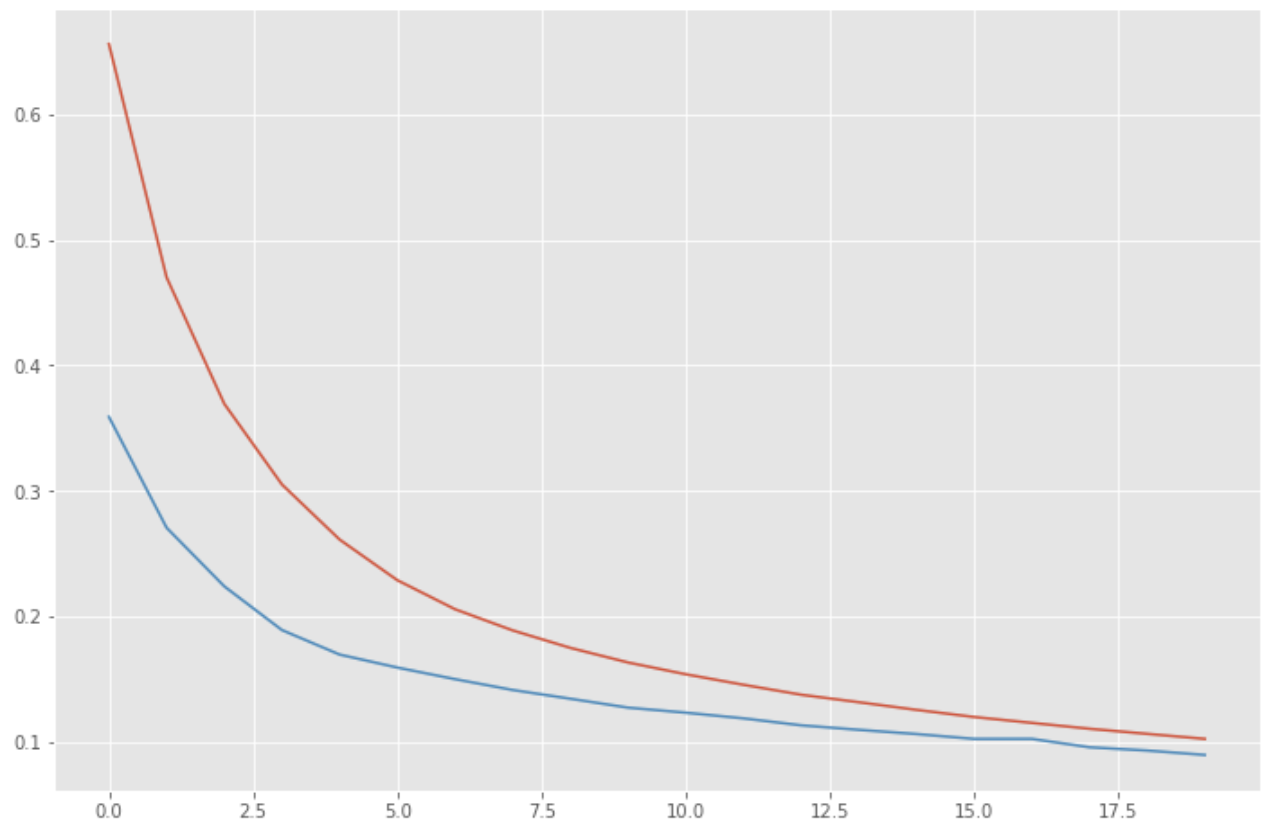
誤差の推移を確認します。
loss = history.history['loss']
vloss = history.history['val_loss']
plt.figure(figsize=(12, 8))
plt.plot(np.arange(len(loss)), loss)
plt.plot(np.arange(len(vloss)), vloss)
plt.show()
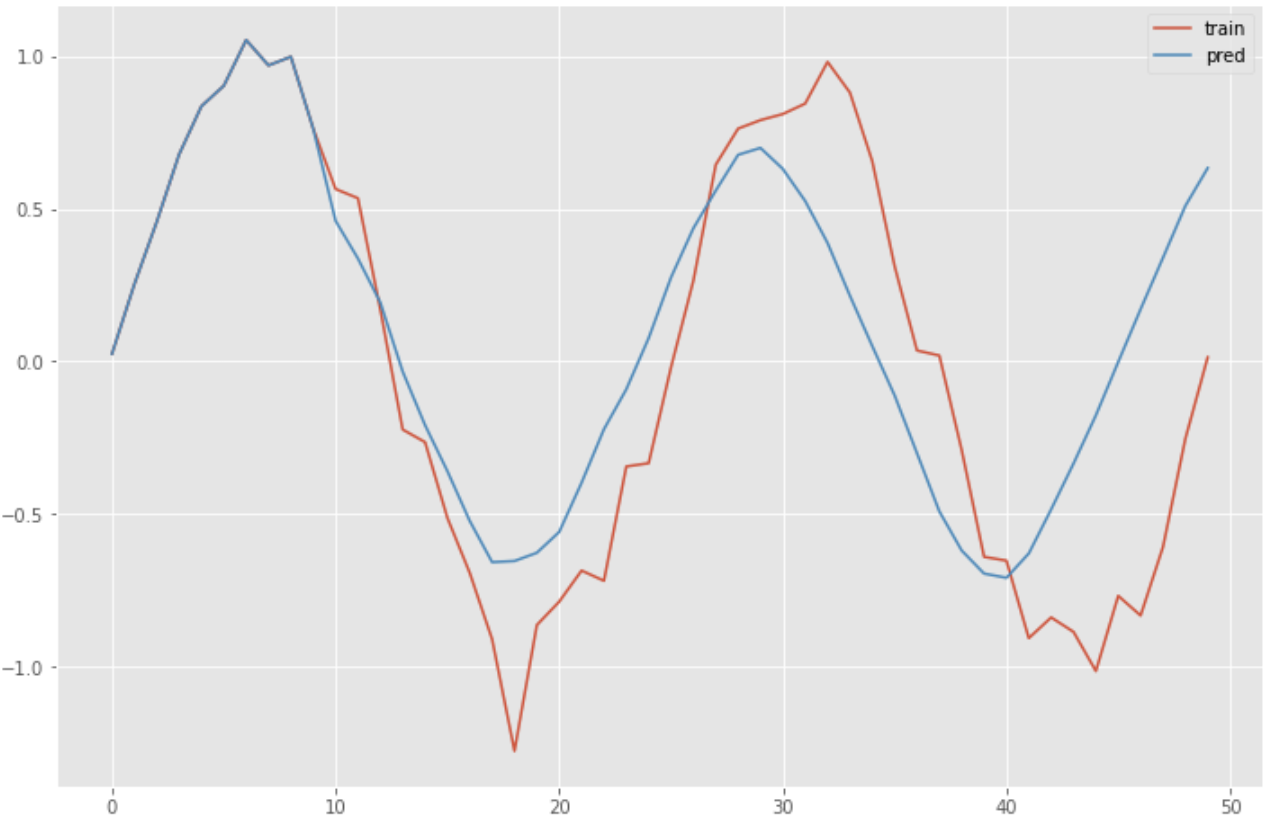
RNNの学習済みモデルを使って予測を行います。
predicted = x[0].reshape(-1)
for i in range(0, n_sample):
y = model.predict(predicted[-n_rnn:].reshape(1, n_rnn, 1))
predicted = np.append(predicted, y[0][n_rnn-1][0])
plt.figure(figsize=(12, 8))
plt.plot(np.arange(len(sin_data)), sin_data, label="training")
plt.plot(np.arange(len(predicted)), predicted, label="predicted")
plt.legend()
plt.show()
参考