片側検定

片側検定は、標本分布の一方の側にのみ棄却領域がある仮説検定のタイプです。

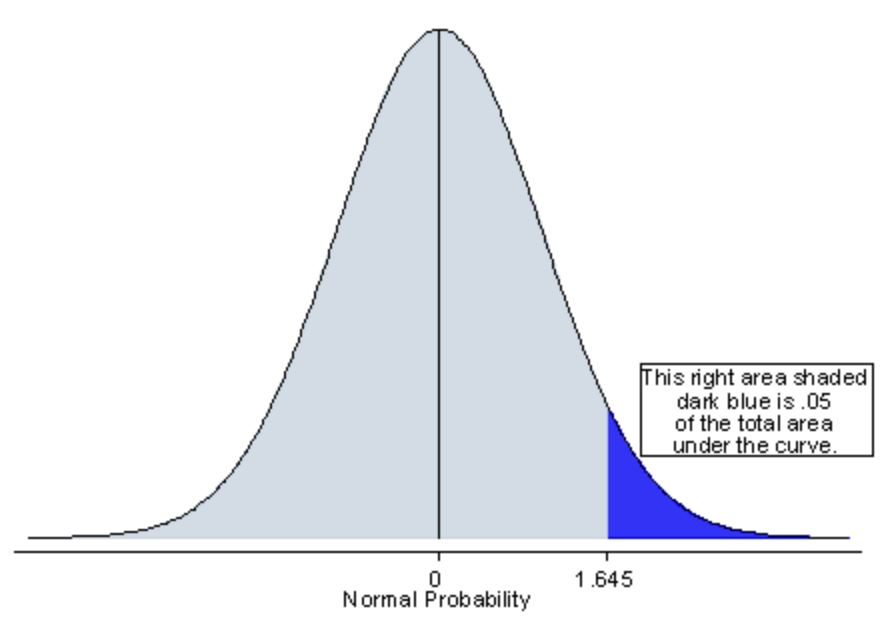
FAQ: WHAT ARE THE DIFFERENCES BETWEEN ONE-TAILED AND TWO-TAILED TESTS?

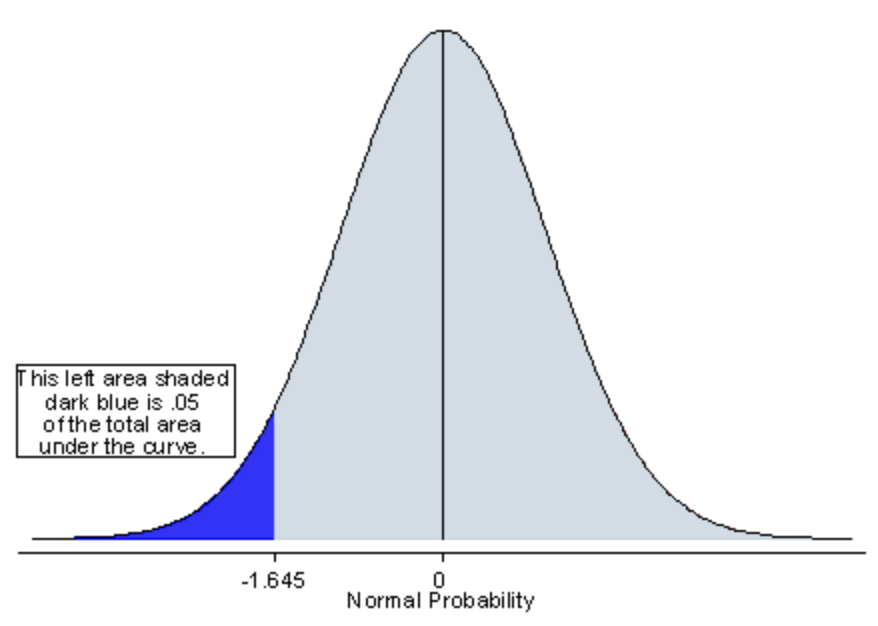
FAQ: WHAT ARE THE DIFFERENCES BETWEEN ONE-TAILED AND TWO-TAILED TESTS?

例えば、ある製品の製造プロセスの改良が耐久性を増加させると信じている研究者として想像してみてください。この場合、耐久性の低下については心配していませんが、増加には関心があります。この仮説を検証するためには、片側検定を使用します。

このシナリオでは、帰無仮説 (H_0) は「改良によって製品の耐久性は増加しない」と述べられ、対立仮説 (H_1) は「改良によって製品の耐久性は増加する」となります。なお、対立仮説は方向性があり、「より大きい」という効果を示唆しています。

片側検定の選択は、効果の方向が事前に理論、過去の研究、または実践的な考慮に基づいて予測される場合に正当化されます。

有意水準

片側検定では、全体の有意水準 \alpha（例えば、0.05）が分布の片側（左側または右側）に配置されます。0.05の \alpha を用いる場合、棄却領域（帰無仮説を棄却する領域）は興味のある方向における分布のもっとも極端な5%を含みます。

両側検定

一方、両側検定は、棄却領域が標本分布の両側にある方法です。つまり、関係性が両方の方向に存在する可能性を検定しています。

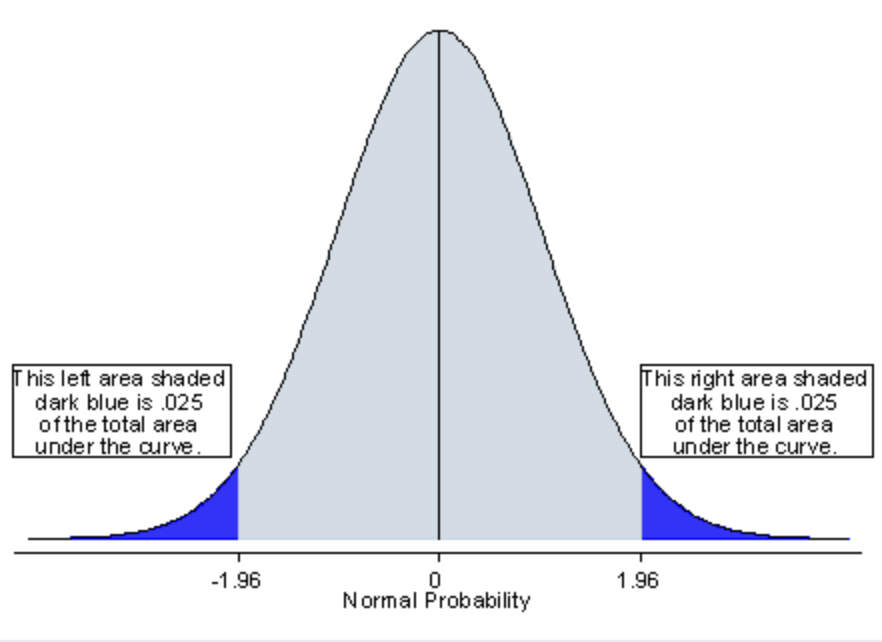
FAQ: WHAT ARE THE DIFFERENCES BETWEEN ONE-TAILED AND TWO-TAILED TESTS?

例えば、新薬物が血圧に与える影響を研究している科学者として想像してみます。薬物が血圧を上昇させる可能性も下降させる可能性もあると疑っており、両方の結果に関心があります。この場合、両側検定が適切です。

ここでは、帰無仮説（H_0）は「薬物は血圧に影響を与えない」とし、対立仮説（H_1）は「薬物は血圧に影響を与える」とします。対立仮説は効果の方向を特定せず、単に効果が存在することを示しています。

両側検定の選択は、効果の方向が不明であるか、または研究の文脈で考慮されない場合に適しています。

有意水準

両側検定では、有意水準 \alpha が分布の両側に分割されます。したがって、0.05の \alpha を用いる場合、棄却領域は分布の両端におけるもっとも極端な値の2.5%を含みます。両側の合計で5%になります。つまり、帰無仮説の下で期待される値よりも有意に高い値または有意に低い値の場合に帰無仮説を棄却します。

例: 片側検定と両側検定の実施

片側検定と両側検定の概念をより具体的に説明するために、実際の例を考えてみます。新しい教授法の生徒の数学の成績に与える影響を調査する研究者であると想像してください。

研究問題の設定

研究問題は次のようになります。

新しい教授法は生徒の数学の成績に影響を与えるか？

仮説検定の選択

研究問題に基づいて、片側検定と両側検定のどちらかを選択する必要があります。効果の方向（つまり、新しい教授法が数学の成績を向上させるのか悪化させるのか）について事前の知識や期待がない場合（つまり、新しい教授法が数学の成績を改善させるか悪化させるかがわからない場合）、両側検定が適切です。

仮説の設定

両側検定の場合、帰無仮説（H_0）は「新しい教授法は生徒の数学の成績に影響を与えない」とし、対立仮説（H_1）は「新しい教授法は生徒の数学の成績に影響を与える」となります。対立仮説は効果の方向を特定せず、単に効果が存在することを示しています。

今度は、新しい教授法が生徒の数学の成績を向上させるという事前の知識や強力な理論的根拠があるとします。この場合、片側検定が適切です。

片側検定の場合、帰無仮説（H_0）は「新しい教授法は生徒の数学の成績を改善しない」とし、対立仮説（H_1）は「新しい教授法は生徒の数学の成績を改善する」となります。

統計的分析の実施

新しい教授法を使用したグループと従来の教授法を使用したグループからデータを収集した後、適切な統計的検定を実施します。

もしも両側検定を選んだ場合、数学の成績の間に有意な差があるかどうかを調べます。効果の方向に関係なく、有意な結果は新しい教授法が数学の成績に影響を与えることを示唆します。

もしも片側検定を選んだ場合、新しい教授法を使用したグループの数学の成績が従来の教授法を使用したグループよりも有意に向上しているかを調べます。有意な結果は、新しい教授法が数学の成績を改善するという仮説を支持します。

結果の解釈

統計的分析を実施した後、結果を研究問題と選択した仮説検定の文脈で解釈する必要です。結果が有意であれば、新しい教授法が生徒の数学の成績に与える影響について結論を導くことができます。結果が有意ではない場合、帰無仮説を棄却する根拠が不十分であるため、対立仮説を支持する証拠が得られなかったと結論付ける必要があります。