損失関数とは

機械学習において、損失関数とは、モデルによる出力された「予測値」と、実際の「正解値」とのズレの大きさを計算するための関数になります。つまり、損失関数はデータに対してモデルがどれだけ適合していないかという、モデルの「悪さ」を示す指標になります。ニューラルネットワークの学習では、損失関数を最小化するパラメータ（重みやバイアス）を探索し、モデルを最適化します。

損失関数には様々なものがあります。以下が例になります。

• 平均二乗誤差（MSE：Mean Squared Error）
• 平均絶対誤差（MAE）
• 平均二乗誤差の平方根（RMSE）
• 平均二乗対数誤差（MSLE）
• 交差エントロピー誤差
• Huber損失
• ポアソン損失

今回は平均二乗誤差と交差エントロピー誤差について紹介します。

平均二乗誤差

平均二乗誤差は、出力値と正解値の差を二乗し、全ての出力層のニューロンで総和をとったものになります。平均二乗誤差はEを誤差、y_kを出力層の各出力値、t_kを正解値として次の式で定義されます。

平均二乗誤差は正解や出力が連続的な数値であるケースに向いているため、回帰問題でよく使用されます。

Pythonを用いて平均二乗誤差は次のように実装することができます。

def square_sum(y, t):
    return 1.0/2.0 * np.sum(np.square(y - t))

この関数を手書き数字認識の例でテストしてみます。まずは次のようなソフトマックス関数の出力値を用意します。

y = np.array([0.1, 0,6, 0,2, 0.05, 0.05, 0, 0, 0, 0, 0])

ソフトマックス関数の出力は確率として解釈することができるので、「0」の確率が0.1、「1」の確率が0.6ということを表しています。

次に、正解データを用意します。ここでは、手書き数字認識の正解が「0」の場合と「1」の場合の正解データをそれぞれを用意します。

t1 = np.array([1, 0, 0, 0, 0, 0, 0, 0, 0, 0])
t2 = np.array([0, 1, 0, 0, 0, 0, 0, 0, 0, 0])

正解データは、正解ラベルを1としてそれ以外を0で表すone-hot表現となっています。

出力値と正解データを用いて平均二乗誤差を算出します。

import numpy as np

def square_sum(y, t):
    return 1.0/2.0 * np.sum(np.square(y - t))

y = np.array([0.1, 0.6, 0.2, 0.05, 0.05, 0, 0, 0, 0, 0])

t1 = np.array([1, 0, 0, 0, 0, 0, 0, 0, 0, 0])
t2 = np.array([0, 1, 0, 0, 0, 0, 0, 0, 0, 0])

print('y and t1:', square_sum(y, t1))
print('y and t2:', square_sum(y, t2))

y and t1: 0.6074999999999999
y and t2: 0.10750000000000003

出力yは「1」の確率がもっとも高いので、「1」が正解ラベルであるt2との誤差が小さくなっていることが分かります。

交差エントロピー誤差

交差エントロピー誤差は二つの分布の間のズレを表す尺度であり、分類問題でよく使用されます。交差エントロピー誤差は次の式で表されます。

分類問題における正解値は、正解レベルを1としてそれ以外を0で表すone-hot表現になります。そのため、右辺の\sum内でt_kが1の項のみ誤差に影響を与えることになり、t_kが0の項の影響は無視されます。

次に\log (y_k)について考えます。自然対数\log xは、 xが１の時に「0」となり、xが「0」に近づくつれて無限に小さくなるという性質を持っています。自然対数の絶対値をとると、ニューラルネットワークの出力 y に対する -\log x のグラフは、次のようになります。

%matplotlib inline

import matplotlib.pyplot as plt
y = np.arange(0, 1.01, 0.01)
delta = 1e-7
loss = -np.log(y + delta)
plt.plot(y, loss)
plt.xlim(0, 1)
plt.xlabel('x')
plt.ylim(0, 5)
plt.ylabel('- log x')
plt.show()

-\log x は x が1の時は0で、xが0に近づくにつれて無限に大きくなります。つまり、出力が正解に近づくほど誤差が0に近づき、出力が正解から離れるほど誤差がどこまでも大きくなります。このように、交差エントロピー誤差は自然対数の性質を用いて損失関数を導きます。

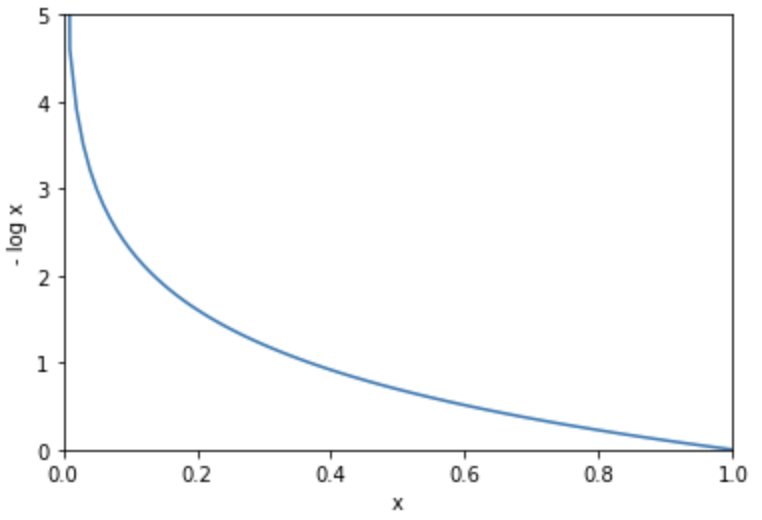
交差エントロピーは、出力値と正解値の隔離が大きい時に学習速度が速いというメリットがあります。上記の通り、出力が正解と隔離すると誤差が無限に増大するため、このような場合に学習が高速になります。

交差エントロピー誤差はPythonで次のように実装することができます。

import numpy as np

def cross_entropy(y, t):
    return - np.sum(t * np.log(y + 1e-7))

yに微小な値1e-7を加えている理由は、log関数の中身が0になり、自然対数が無限小に発散してしまうことを防止するためです。

平均二乗誤差の例で使用した出力と正解データを用いて交差エントロピー誤差を算出します。

import numpy as np

def cross_entropy(y, t):
    return - np.sum(t * np.log(y + 1e-7))

y = np.array([0.1, 0.6, 0.2, 0.05, 0.05, 0, 0, 0, 0, 0])

t1 = np.array([1, 0, 0, 0, 0, 0, 0, 0, 0, 0])
t2 = np.array([0, 1, 0, 0, 0, 0, 0, 0, 0, 0])

print('y and t1:', cross_entropy(y, t1))
print('y and t2:', cross_entropy(y, t2))

y and t1: 2.302584092994546
y and t2: 0.510825457099338

出力と正解データとの誤差を損失関数として表現することができました！