活性化関数とは

ニューラルネットワークにおける活性化関数とは、あるニューロンから次のニューロンへと出力する際に、入力値を別の数値に変換して出力する関数のことです。ニューロンへの入力と重み積の総和にバイアス足し合わせた統合された値を、ニューロンの興奮状態を表す信号に変換します。活性化関数が無いとニューロンの演算は単なる積の総和になってしまい、ニューラルネットワークの表現力が失われてしまいます。

活性化関数には様々な種類が存在します。今回は代表的な活性化関数を紹介します。

ステップ関数

ステップ関数は、階段状の関数です。次の式で表されます。

ステップ関数は、Pythonで実行すると次のようなコードになります。

import numpy as np
import matplotlib.pyplot as plt

def step_function(x):
    return np.where(x<=0, 0, 1)

x = np.linspace(-5, 5)
y = step_function(x)

plt.plot(x, y)
plt.show()

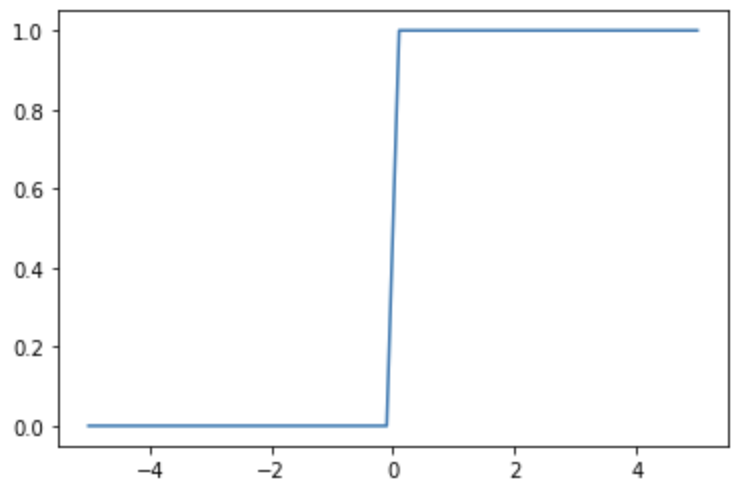
ステップ関数はニューロンの興奮状態を0か1でシンプルに表現することができる反面、0 と 1 の中間の状態を表現できないという欠点があります。

シグモイド関数

シグモイド関数は、0と1の間を滑らかに変化する関数です。次の式で表されます。

シグモイド関数は、Pythonで実行すると次のようなコードになります。

import numpy as np
import matplotlib.pylab as plt

def sigmoid_function(x):
    return 1/(1+np.exp(-x))

x = np.linspace(-5, 5)
y = sigmoid_function(x)

plt.plot(x, y)
plt.show()

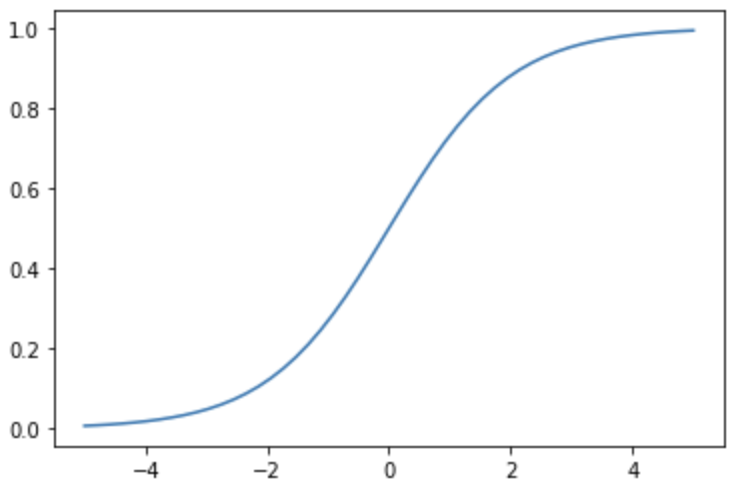
シグモイド関数はステップ関数と比べて滑らかであり、0と1の中間を表現することができます。また、シグモイド関数は、微分が扱いやすいという特徴があります。

tanh 関数

tanh関数は、-1と1の間を滑らかに変化する関数です。曲線の形状はシグモイド関数に類似していますが、tanh関数は0を中心とした対称になっています。tanh関数は、次の式で表されます。

tanh関数は、Pythonで実行すると次のようなコードになります。

import numpy as np
import matplotlib.pylab as plt

x = np.linspace(-5, 5)
y = np.tanh(x

plt.plot(x, y)
plt.show()

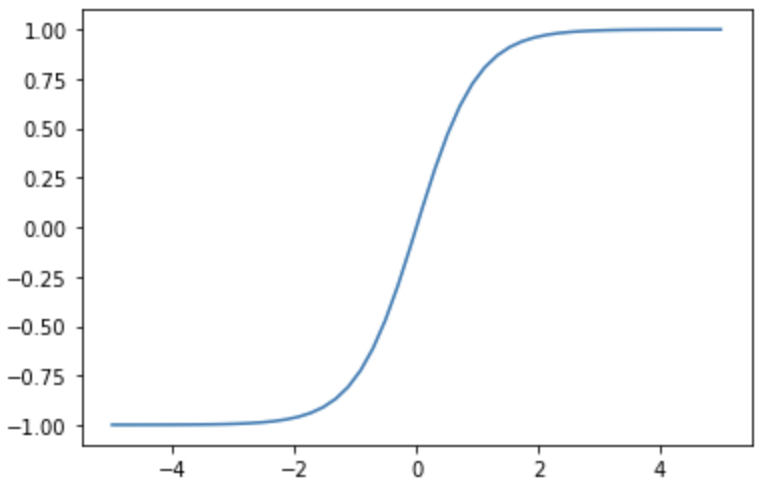
ReLU 関数

ReLU関数は、入力 x が負であれば出力y が0に、x が正であれば y が x となる関数です。
ReLU関数は、次の式で表されます。

ReLU関数は、Pythonで実行すると次のようなコードになります。

import numpy as np
import matplotlib.pylab as plt

x = np.linspace(-5, 5)
y = np.where(x <= 0, 0, x)

plt.plot(x, y)
plt.show()

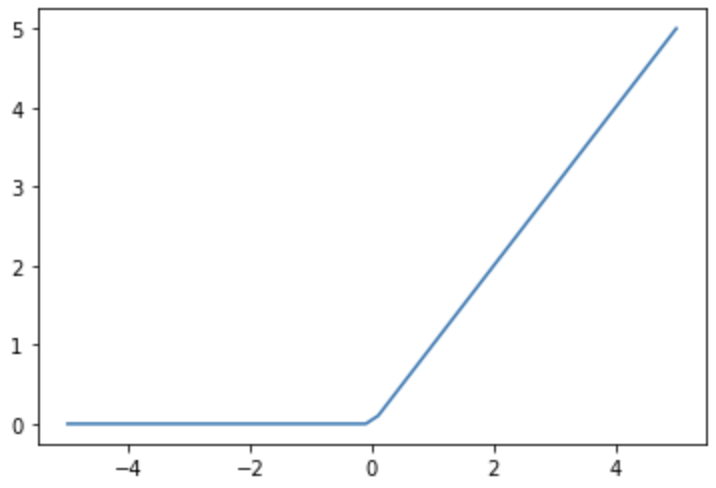
ReLU関数はシンプルでありながら、層の数が多くなっても安定した学習ができるため、出力層以外の活性化関数としてよく用いられています。

恒等関数

恒等関数は、入力をそのまま出力として返す関数です。次の式で表されます。

恒等関数は、Pythonで実行すると次のようなコードになります。

import numpy as np
import matplotlib.pylab as plt

x = np.linspace(-5, 5)
y = x

plt.plot(x, y)
plt.show()

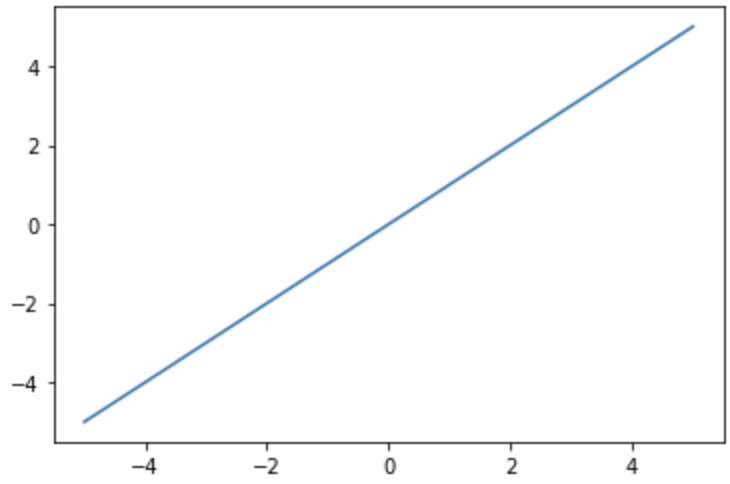
恒等関数は出力の範囲に制限が無く連続的であり、連続的な数値を予測するのに適していることから回帰問題で使われることが多いです。

ソフトマックス関数

ソフトマックス関数は、分類問題に適した活性化関数です。活性化関数の出力を y、入力を x、同じ層のニューロンの数をnとするとソフトマックス関数は次の式で表されます。

また、ソフトマックス関数の次の特性があります。

• 同じ層の出力の総和は1になる
• 0<y<1 の値が出力される

このような性質から、ソフトマックス関数は多クラス分類の出力層として利用されます。

ソフトマックス関数は、次のコードで実装することができます。

import numpy as np

def softmax_function(x):
    return np.exp(x)/np.sum(np.exp(x))

y = softmax_function(np.array([1,2,3]))
print(y)

[0.09003057 0.24472847 0.66524096]