2022-10-02

K-Meansクラスタリング

Machine Learning

Clustering

Python

sklearn

K-Meansクラスタリングとは

K-Meansクラスタリングは、データセットをK個の異なるクラスタに分割するために広く使用される教師なし学習です。このアルゴリズムは、クラスタ内の変動を最小限に抑え、クラスタ間の変動を最大化する方法で、似たデータポイントを特徴値に基づいてグループ化することを目的としています。

K-Meansアルゴリズム

目的関数

K-Meansアルゴリズムは、クラスタ内の総二乗和、または目的関数またはコスト関数を最小化することを目的としています。数学的には、目的関数は次のように定義されます。

$J(C_1, C_2, \dots, C_K) = \sum_{i=1}^{K} \sum_{x \in C_i} ||x - \mu_i||^2$

ここで、 $K$ はクラスタの数、 $C_i$ は $i$ 番目のクラスタ、 $x$ はクラスタ $C_i$ に割り当てられたデータポイントであり、 $\mu_i$ はクラスタ $C_i$ のデータポイントの重心(平均)です。目標は、最適なクラスタ割り当てと重心を見つけ、目的関数を最小化することです。

K-Meansアルゴリズムの手順

K-Meansアルゴリズムは、次の手順で構成されています。

初期化
データポイントから $K$ 個の初期重心をランダムに選択します。これらの重心は、実際のデータポイントまたはデータ範囲内でランダムに生成することができます。
割り当て
各データポイントをもっとも近い重心に割り当てます。データポイントと重心の距離は通常、ユークリッド距離を使用して測定されますが、他の距離尺度も使用できます。
更新
重心を新しいデータポイントに割り当てられたクラスタの全てのデータポイントの平均値を取ることによって計算します。
収束
重心の位置が大幅に変化しなくなるか、事前定義された反復回数に達するまで、手順2と手順3を繰り返します。

アルゴリズムは初期重心の配置に敏感であり、異なる初期化は異なる最終的なクラスタ割り当てにつながる可能性があります。この問題を緩和するために、アルゴリズムはしばしば異なる初期化で複数回実行され、最終的なクラスタリング結果はもっとも低い目的関数値に基づいて選択されます。

正しいクラスタ数の選択

適切なクラスタ数(K)を選択することは、K-Meansアルゴリズムのパフォーマンスにとって重要です。Kを小さくするとアンダーフィッティングの結果になり、大きくするとオーバーフィッティングの結果になります。この章では、最適なK値を決定するための3つの人気のある方法、エルボー法、シルエット法、ギャップ統計について説明します。

エルボー法

エルボー法は、説明された変動（慣性）をクラスタの数(K)の関数としてプロットし、プロット内の「肘」点を特定するヒューリスティック技術です。慣性とは、各データポイントとその割り当てられた重心の間の二乗距離の合計です。 Kが増加するにつれて、慣性は減少しますが、減少率は低下します。肘点は、慣性の減少率が著しく低下し始めるKの値を示し、より多くのクラスタを追加しても実質的な改善が得られないことを示唆しています。

エルボー法を適用する手順:

Kの異なる値でK-Meansアルゴリズムを実行。通常、1からあらかじめ定義された最大値までの範囲で値を変更します。
各Kの慣性を計算
Kの関数として慣性をプロット
プロット内の肘点を特定し、それに対応するKの最適値を決定

シルエット法

シルエット法は、各データポイントのシルエットスコアを計算してクラスタリングの品質を測定する方法です。シルエットスコアは、-1から1までの範囲で、データポイントが自分自身のクラスタに比べて他のクラスタにどの程度似ているかを示す指標です。

高いシルエットスコアは、データポイントが自分自身のクラスタに適合し、他のクラスタに適合していないことを示します。全てのデータポイントの平均シルエットスコアは、クラスタリング品質の全体的な評価を提供します。

シルエット法を適用する手順:

Kの異なる値でK-Meansアルゴリズムを実行。通常、2からあらかじめ定義された最大値までの範囲で値を変更します。
各データポイントのシルエットスコアを計算し、各K値の平均シルエットスコアを計算
平均シルエットスコアをKの関数としてプロット
平均シルエットスコアが最大となるKの値を特定

ギャップ統計

ギャップ統計は、最適なクラスタ数(K)を推定するために使用される別の技術です。これは、異なるKの総クラスタ内変動を、ヌル基準分布の期待値と比較することによって推定します。

ギャップ統計を適用する手順:

Kの異なる値でK-Meansアルゴリズムを実行。通常、1からあらかじめ定義された最大値までの範囲で値を変更します。
各K値の総クラスタ内変動（慣性）を計算
ヌル基準分布を生成し、元のデータセットと同じ次元と範囲のランダムデータセットを作成
ランダムデータセット上でK-Meansアルゴリズムを実行し、各K値の総クラスタ内変動（慣性）を計算
観察された慣性の対数とヌル基準分布の期待慣性の対数の差をギャップ統計として、各Kの値に対して計算
ギャップ統計が最大となるKの値を特定

PythonにおけるK-Meansの実装

Pythonを使用してアヤメのデータセットにK-Meansクラスタリングアルゴリズムを実装し、クラスタリング結果を可視化します。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasets
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score

# Load Iris dataset
iris = datasets.load_iris()
data = iris.data
feature_names = iris.feature_names

# Create a DataFrame
df = pd.DataFrame(data, columns=feature_names)

# Elbow Method to determine the optimal number of clusters (K)
inertias = []
K_range = range(1, 11)

for K in K_range:
    kmeans = KMeans(n_clusters=K, random_state=42)
    kmeans.fit(df)
    inertias.append(kmeans.inertia_)

plt.figure(figsize=(8, 5))
plt.plot(K_range, inertias, marker='o', color='blue', alpha=0.5)
plt.xlabel("Number of Clusters (K)")
plt.ylabel("Inertia")
plt.title("Elbow Method for Optimal K")
plt.show()

# Silhouette Method to determine the optimal number of clusters (K)
silhouette_scores = []

for K in range(2, 11):
    kmeans = KMeans(n_clusters=K, random_state=42)
    kmeans.fit(df)
    silhouette_scores.append(silhouette_score(df, kmeans.labels_))

plt.figure(figsize=(8, 5))
plt.plot(range(2, 11), silhouette_scores, marker='o', color='blue', alpha=0.5)
plt.xlabel("Number of Clusters (K)")
plt.ylabel("Average Silhouette Score")
plt.title("Silhouette Method for Optimal K")
plt.show()

# Based on the visualizations, choose the optimal K value
optimal_K = 3

# Perform K-Means clustering with the optimal K value
kmeans = KMeans(n_clusters=optimal_K, random_state=42)
kmeans.fit(df)
labels = kmeans.labels_
df['Cluster'] = labels

# Visualize the clustering result
plt.figure(figsize=(10, 6))
sns.scatterplot(x=df.iloc[:, 0], y=df.iloc[:, 1], hue=df['Cluster'], palette="deep", s=100)
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], c='red', marker='x', label='Centroids', s=200)
plt.xlabel(feature_names[0])
plt.ylabel(feature_names[1])
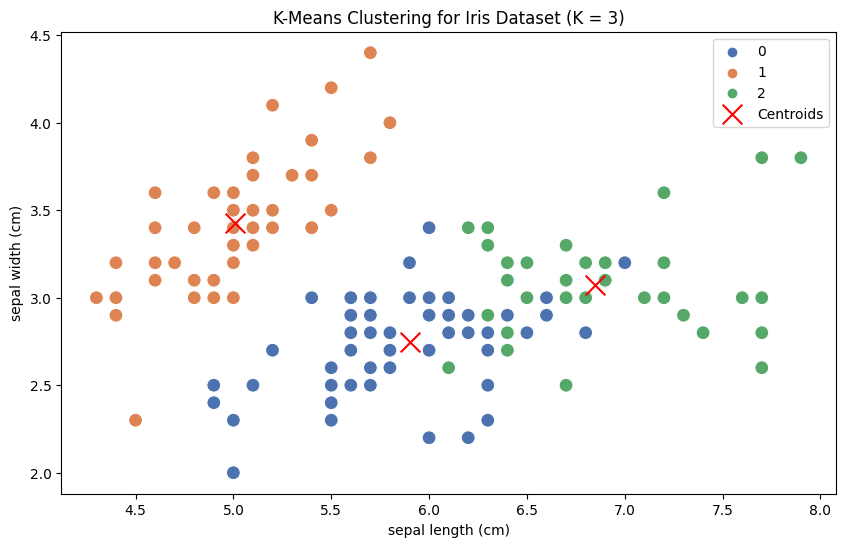
plt.title("K-Means Clustering for Iris Dataset (K = 3)")
plt.legend()
plt.show()

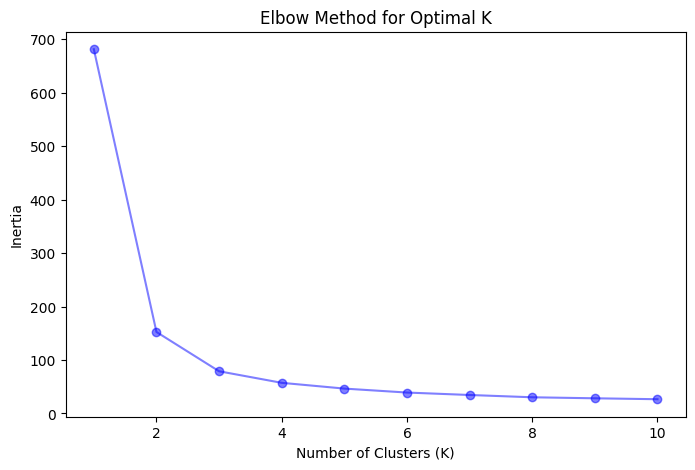
Elbow method
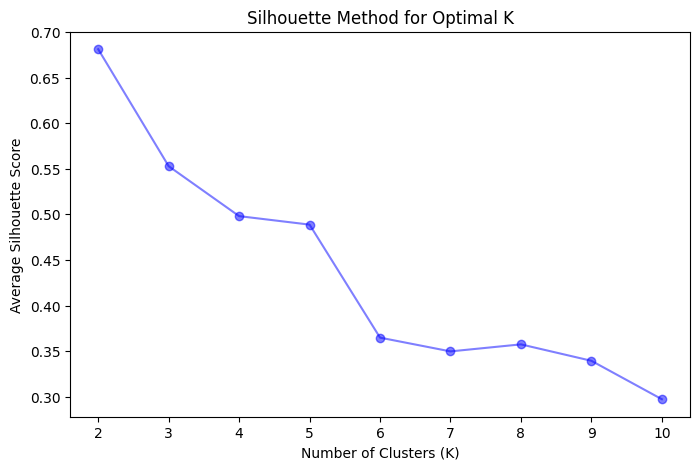
Silhouette method
K-Means method

このコードはまず、アヤメのデータセットを読み込んでDataFrameに変換します。次に、エルボー法とシルエット法を使用して最適なクラスタ数（K）を可視化します。可視化に基づいて、最適な値として $K = 3$ を選択します。

最後に、最適なK値でK-Meansクラスタリングを実行し、散布図を使用して生成されたクラスタを可視化します。異なる色が異なるクラスタを表し、赤い「x」マーカーが各クラスタの重心を表します。