階層的クラスタリングとは

階層的クラスタリングは、類似したオブジェクトを類似性と相違点に基づいてクラスタやサブグループにグループ化するタイプの教師なし機械学習アルゴリズムです。階層的クラスタリングの目的は、クラスタの階層構造またはツリー状の構造を作成することで、ツリーの下位レベルのクラスタは、上位レベルのものよりもお互いに似ています。

デンドログラム

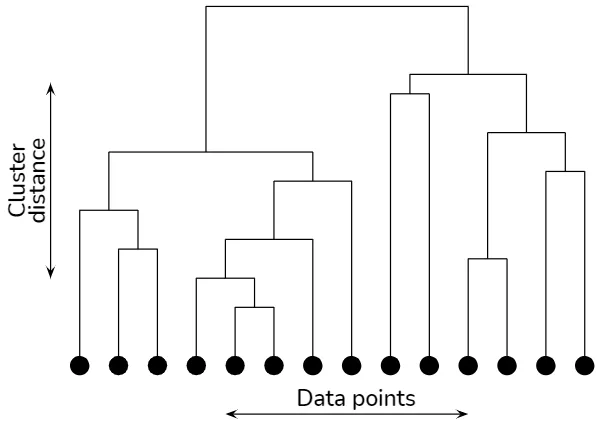
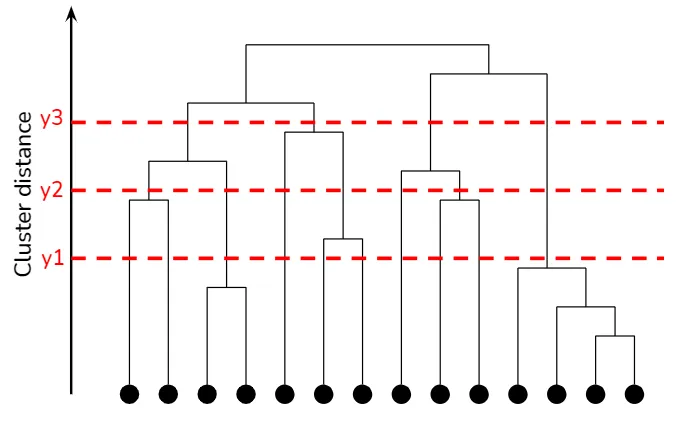
デンドログラムは、クラスタの階層構造を視覚的に表現する木構造のダイアグラムです。デンドログラムでは、各ノードがクラスタを表し、エッジがクラスタ間の距離または類似性を表します。エッジの高さは、結合または分割されるクラスタ間の類似度を示します。デンドログラムを調べることで、さまざまな粒度レベルでのクラスタリング構造を観察し、ドメイン知識や他の基準に基づいて最適なクラスタの数を決定できます。

Hierarchical clustering explained

Hierarchical clustering explained

集積的アプローチと分割的アプローチ

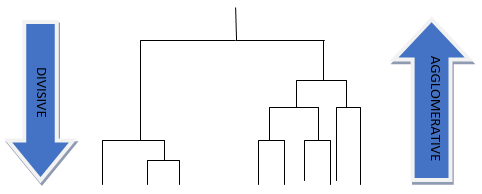
階層的クラスタリングには、集積的アプローチと分割的アプローチの2つの主要な方法があります。

集積的階層的クラスタリング、またはボトムアップクラスタリングとも呼ばれます。このアプローチは、各データポイントを単一のクラスタとして考慮して開始します。各ステップで、もっとも近い2つのクラスタが結合され、全てのデータポイントが1つのクラスタに所属するまでプロセスが繰り返されます。ヒエラルキーは、異なるレベルでのマージを示す木構造のダイアグラムで表されます。

分割的階層的クラスタリング、またはトップダウンクラスタリングは、全てのデータポイントを単一のクラスタとして開始し、再帰的にクラスタを小さなクラスタに分割していきます。アルゴリズムは、各ステップで最大またはもっとも異質なクラスタを特定し、選択した二分法に基づいて2つのサブクラスタに分割します。このプロセスは、各データポイントが自分自身のクラスタを形成するまで続けられます。結果は、階層構造のクラスタを表すデンドログラムによって表されます。集積的アプローチと同様です。

Hierarchical Clustering Analysis

集積的階層的クラスタリング

ボトムアップアプローチ

集積的階層的クラスタリングは、個々のデータポイントを別々のクラスタとして始め、それらを大きなクラスタにまとめていきます。アルゴリズムは、もっとも類似度が高いまたはもっとも近いクラスタのペアを反復的に結合していき、全てのデータポイントが1つのクラスタに属するようにします。結果は、デンドログラムで表されるクラスタの階層構造です。

リンク法

集積的階層的クラスタリングにおけるクラスタのマージプロセスは、リンク法の選択によって異なります。リンク法は、クラスタ間の距離または類似度を定義し、各ステップでどのクラスタをマージするかを決定します。一般的なリンク法には、次のものがあります。

シングルリンク

シングルリンクでは、2つのクラスタ間の距離は、2つのクラスタから1つずつのデータポイントを選び、その最小距離とします。この方法は、伸びた鎖状のクラスタを生成する傾向があり、ノイズや外れ値に敏感です。

コンプリートリンク

コンプリートリンクは、2つのクラスタ間の距離を、2つのクラスタから1つずつのデータポイントを選び、その最大距離とします。この方法は、コンパクトでよく区別されたクラスタを生成しますが、クラスタの初期選択に敏感であり、過剰な分割を引き起こす可能性があります。

アベレージリンク

アベレージリンクは、2つのクラスタ間の距離を、2つのクラスタから全てのデータポイントの間の平均距離とします。この方法は、バランスの取れた形状とサイズのクラスタを生成し、シングルリンクやコンプリートリンクに比べてノイズや外れ値に対して少なく感受性があります。

セントロイドリンク

セントロイドリンクは、2つのクラスタ間の距離を、それぞれのクラスタのデータポイントの平均ベクトルであるセントロイド間の距離とします。この方法は、比較的コンパクトでバランスの取れたサイズのクラスタを生成します。しかし、マージされたクラスタのセントロイドが大幅に移動する「セントロイドシフト現象」に影響を受ける可能性があり、最適なクラスタリング結果が得られない可能性があります。

Ward法

Ward法は、合計内部分散を最小化することによってクラスタをマージします。つまり、もっとも小さな平方和の増加になるようなクラスタをマージします。この方法は、ほぼ等しいサイズのクラスタがあるデータに適しており、コンパクトで球状のクラスタを生成する傾向があります。

分割的階層的クラスタリング

トップダウンアプローチ

分割的階層的クラスタリングは、全てのデータポイントを単一のクラスタとして開始し、クラスタを小さなサブクラスタに再帰的に分割していきます。アルゴリズムは、各ステップで最大またはもっとも異質なクラスタを特定し、選択した二分法に基づいて2つのサブクラスタに分割します。このプロセスは、各データポイントが自分自身のクラスタを形成するまで続けられます。結果は、集積的アプローチと同様にデンドログラムによって表されます。

二分法

分割的階層的クラスタリングにおける二分法の選択によって、各ステップでクラスタがどのように分割されるかが決まります。文献にはさまざまな二分法が提案されており、もっとも一般的なもののいくつかは次のとおりです。

• K-meansまたはK-medoidsに基づく
  クラ
  スタをK=2として、K-meansまたはK-medoidsアルゴリズムを使用してクラスタを2つのサブクラスタに分割します。

• スペクトルクラスタリングに基づく
  グラフラプラシアンの固有ベクトルに基づいてクラスタを分割します。ラプラシアンは、データの接続構造を捉えます。

• PCAに基づく
  データの最初の主成分の方向に沿ってクラスタを分割します。これは、データの最大の分散を捉えます。

• 最大直径に基づく
  最大距離を持つデータポイントのペアを見つけ、これら2つの点に近い点を選択して残りの点を分割して、クラスタを2つのサブクラスタに分割します。

Pythonでの階層的クラスタリングの実装

この章では、Pythonで階層的クラスタリングを実装する方法を示します。公開データセットを使用し、さまざまなリンク法を適用し、デンドログラムおよびその他のプロットで結果を視覚化します。

データセットの読み込みと前処理

このデモンストレーションでは、有名なアヤメのデータセットを使用します。データセットには、4つの特徴（がくの長さ、がくの幅、花びらの長さ、花びらの幅）と3つの種（セトサ、バーシクル、バージニカ）が含まれる150のアヤメのサンプルがあります。

まず、データセットを読み込み、データを前処理します。

import numpy as np
import pandas as pd
from sklearn import datasets

# Load the Iris dataset
iris = datasets.load_iris()
X = iris.data
y = iris.target
target_names = iris.target_names

# Create a DataFrame for easier manipulation
df = pd.DataFrame(X, columns=iris.feature_names)
df['species'] = [target_names[i] for i in y]

階層的クラスタリングの実行

次に、Scikit-learnのAgglomerativeClusteringクラスとSciPyライブラリを使用して階層的クラスタリングを実行します。

from sklearn.cluster import AgglomerativeClustering
from scipy.cluster.hierarchy import dendrogram, linkage

# Define the linkage methods to compare
linkage_methods = ['single', 'complete', 'average', 'ward']

# Perform hierarchical clustering with each linkage method
clustering_results = {}
for method in linkage_methods:
    clustering = AgglomerativeClustering(n_clusters=None, distance_threshold=0, linkage=method)
    clustering.fit(X)
    Z = linkage(X, method)
    clustering_results[method] = Z

異なるリンク法のデンドログラムの視覚化

次に、デンドログラムを視覚化します。

import matplotlib.pyplot as plt
import seaborn as sns

sns.set(style='white', rc={'figure.figsize': (8, 5)})

# Plot dendrograms for each linkage method
for method, Z in clustering_results.items():
    plt.figure()
    plt.title(f'Dendrogram for {method.capitalize()} Linkage', fontsize=12)
    dendrogram(Z, truncate_mode='level', p=5, color_threshold=None, above_threshold_color='k', no_labels=True)
    plt.xlabel('Sample Index', fontsize=14)
    plt.ylabel(f'{method.capitalize()} Distance', fontsize=14)
    plt.grid(False)
    sns.despine()
    plt.show()

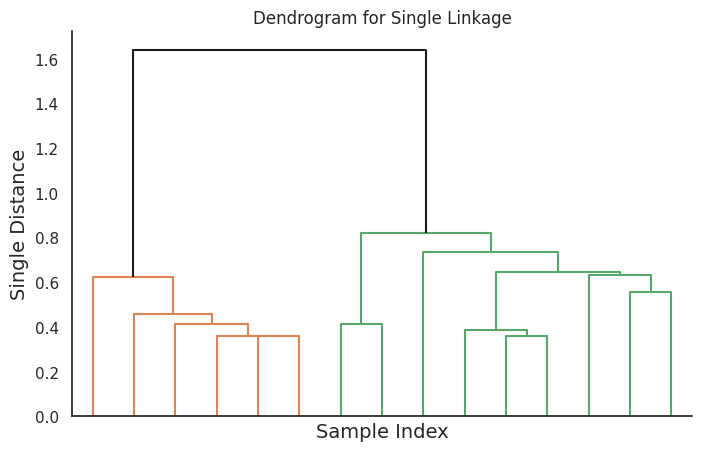
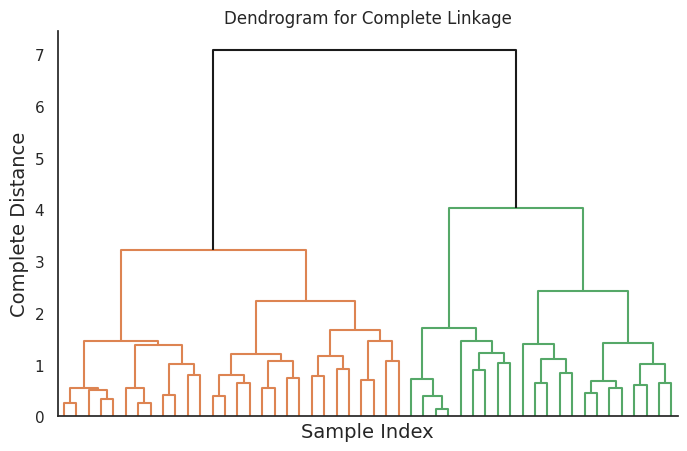
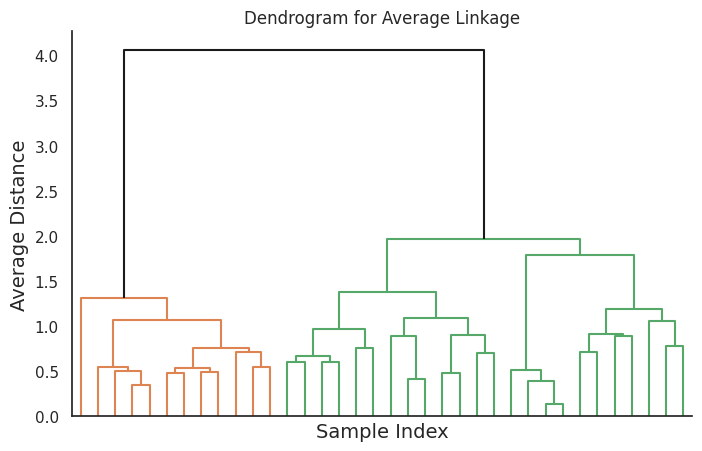
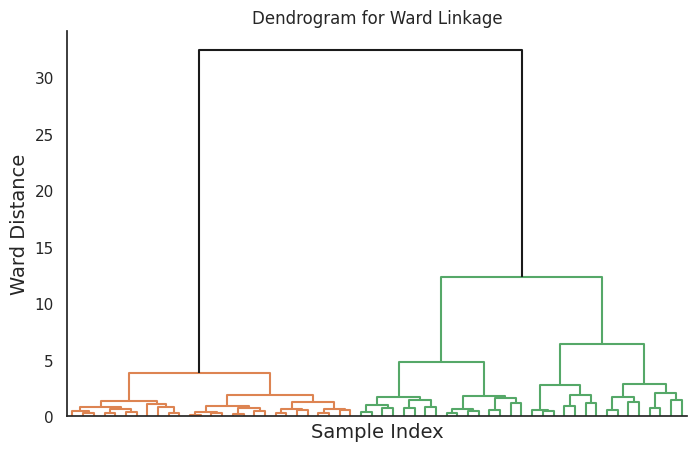
このコードは、異なるリンク法に対応する4つのデンドログラムを生成します。

参考

https://www.mtab.com/blog/what-is-hierarchical-clustering
https://www.educba.com/hierarchical-clustering-analysis/
https://towardsdatascience.com/hierarchical-clustering-explained-e59b13846da8
https://scikit-learn.org/stable/modules/clustering.html#hierarchical-clustering
https://www.youtube.com/watch?v=7xHsRkOdVwo&ab_channel=StatQuestwithJoshStarmer