2022-10-01

クラスタリング

クラスタリングとは

クラスタリングは、データサイエンスにおいて、データの中に隠れたパターンや構造を明らかにするための基本的な技術です。クラスタリングは教師なし学習の一種であり、アルゴリズムはデータのラベルやカテゴリについての事前知識がなくとも、データの基本構造を識別しようと試みます。クラスタリングは、類似したデータポイントを特徴に基づいてグループ化し、一定の均質性を示すクラスタを作成します。これらのクラスタを利用して、データの基本的な関係を理解し、価値のある洞察を導き出すことができます。

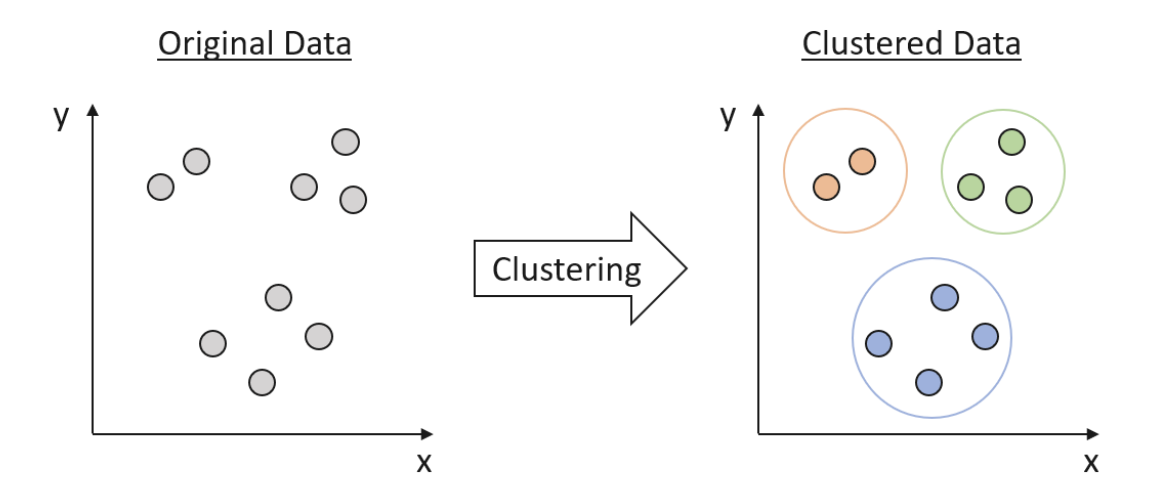
Clustering basics and a demonstration in clustering infrastructure pathways

距離尺度

クラスタリングにおいて、データポイント間の類似性または相違性を測定することは重要な概念です。距離尺度は、データポイント間の差異を定量化し、距離が小さいほど類似性が高いことを示します。一般的に使用される距離尺度には、次のものがあります。

ユークリッド距離
もっとも広く使用されている距離尺度であり、ユークリッド空間内で2つの点間の直線距離を計算します。
マンハッタン距離
L1距離とも呼ばれ、2つの点の座標の絶対差の合計を計算します。
コサイン類似度
2つのベクトル間の角度の余弦を測定し、その類似性を示します。高次元データや、用語の出現頻度ベクトルとして表されるテキストデータに対して特に有用です。
マハラノビス距離
特徴量間の相関関係を考慮し、スケール不変性を持つため、相関または非均質なデータを扱う際に役立ちます。
ジャカード類似度
2つの集合間の類似性を、その共通部分のサイズを全体のサイズで割ったもので測定します。バイナリデータやカテゴリカルデータに対してしばしば使用されます。

クラスタの妥当性と評価

クラスタリング結果の品質を評価することは、選択したアルゴリズムとそのパラメータの効果を判断するために重要です。クラスタの妥当性指標は、クラスタリング結果の品質を評価するための定量的な指標を提供します。これらの指標は、次の3つのカテゴリに分類されます。

内部指標
データの本質的な特性に基づいてクラスタリング結果を評価し、クラスタ内とクラスタ間の距離などが含まれます。例には、シルエット指数、デイビス・ボールディン指数、カリンスキー・ハラバス指数があります。
外部指標
ラベル付きデータから得られた既知の正解とクラスタリング結果を比較します。例には、調整済みランド指数、フォルクス・マローズ指数、ジャッカード指数があります。
相対指標
同じデータセットに対して異なるクラスタリングアルゴリズムまたはパラメータ設定のパフォーマンスを比較します。例には、ギャップ統計量、C指数、ダン指数があります。

クラスタリングアルゴリズム

K-meansクラスタリング

K-meansは、クラスタ内の二乗距離和を最小化することを目的とした、人気のあるパーティションベースのクラスタリングアルゴリズムです。アルゴリズムは、クラスタ重心を表すクラスタ中の全てのデータポイントの平均値として表されるクラスタ重心に対して、データポイントをK個の事前定義されたクラスタの1つに割り当てます。K-meansの主要なステップは次のとおりです。

K個のクラスタ重心をランダムに初期化
各データポイントをもっとも近いクラスタ重心に割り当てる
全てのクラスタ内の全てのデータポイントの平均値を計算してクラスタ重心を更新
収束するまで（つまり、クラスタ重心が変化しなくなる）または事前定義された反復回数に達するまで、ステップ2とステップ3を繰り返す

K-meansはシンプルで高速であり、大規模なデータセットやリアルタイムアプリケーションに適しています。データが分割構造を明確に示す場合、および等方性と凸形状のクラスタを持つ場合には、うまく機能します。ただし、K-meansにはいくつかの制限があります。

ユーザーは事前にクラスタ数（K）を指定する必要があり、事前に知らない場合がある
アルゴリズムはクラスタ重心の初期配置に敏感であり、局所的な最小値に収束することがある。この問題を緩和するために、異なる初期化を持つ複数のランで実行し、クラスタ内二乗距離に基づいて最良の解を選択できます。
K-meansは外れ値やノイズに敏感であり、クラスタ重心に大きな影響を与えることがある
全てのクラスタが似たサイズ、形、密度を持つと仮定しているため、現実のデータには当てはまらない場合がある

階層的クラスタリング

階層的クラスタリングアルゴリズムは、データポイント間の階層的関係を表すツリー状の構造（デンドログラム）を構築します。

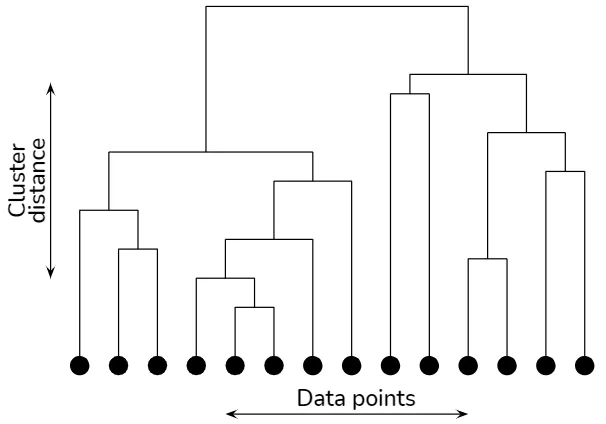
Dendrogram
Hierarchical clustering explained

階層的クラスタリングには、次の2つの主要なタイプがあります。

凝集型（ボトムアップ）
各データポイントを個別のクラスタとして開始し、もっとも近い2つのクラスタを反復的に結合して単一のクラスタを得ます。
分割型（トップダウン）
全てのデータポイントを含む単一のクラスタを開始し、ある基準に基づいてクラスタを再帰的に小さなクラスタに分割します。

クラスタ間の距離を計算する方法を決定する距離メトリックとリンケージ基準の選択は、生成されるデンドログラムに大きな影響を与えます。一般的なリンケージ基準には、シングルリンケージ、コンプリートリンケージ、平均リンケージ、Wardの方法などがあります。

DBSCAN (Density-Based Spatial Clustering of Applications with Noise)

DBSCANは、データポイントの近接性と密度に基づいてデータポイントをグループ化する密度ベースのクラスタリングアルゴリズムです。アルゴリズムは、低い点密度の領域によって分離されたデータポイントの密集領域をクラスタとして定義します。DBSCANには、近傍半径（eps）と密集領域を形成するために必要な最小データポイント数（minPts）の2つのパラメータが必要です。DBSCANアルゴリズムの主なステップは次のとおりです。

各データポイントについて、eps半径内の近傍を決定
データポイントが少なくともminPts個の近傍を持つ場合は、それをコアポイントとしてマークする。そうでない場合は、ノイズポイントとしてマークする。
まだクラスタに割り当てられていない各コアポイントについて、新しいクラスタを作成し、直接および間接的に到達可能な全てのコアポイントをクラスタに再帰的に追加
ノイズポイントをコアポイントのeps半径内にある場合、最寄りのクラスタに割り当てる。それ以外の場合は未割り当てのままにする。

DBSCANはノイズに対して強力であり、ノイズポイントをクラスタから識別して分離できます。また、K-meansや階層的クラスタリングとは異なり、任意の形状と変化する密度を持つクラスタを検出できます。ただし、DBSCANにはepsとminPtsのパラメータを定義する必要があり、これらのパラメータを選択することは困難な場合があります。距離グラフでは、昇順に並べた各データポイントのk番目の最近傍までの距離をプロットすることで、これらのパラメータを選択する一般的なアプローチがあります。

ガウス混合モデル

ガウス混合モデル（GMM）は、複数のガウス分布の混合物としてデータセットを表す生成確率モデルです。期待値最大化（EM）アルゴリズムを使用して、ガウス分布のパラメータと混合比率を推定します。EMアルゴリズムの主なステップは次のとおりです。

ガウス分布パラメータと混合比率を初期化
Eステップ: 現在のパラメータ推定値を考慮して、各データポイントが各ガウス分布に属する事後確率を計算
Mステップ: 事後確率に基づいて、ガウス分布パラメータと混合比率を更新
ステップ2およびステップ3を収束するまでまたは事前に定義された反復回数に達するまで繰り返す

GMMは複雑なデータ分布をモデル化でき、クラスタの共分散構造を自動的に推定できます。ただし、ユーザーは事前にガウス分布（コンポーネント）の数を指定する必要があります。AICやベイズ情報量基準（BIC）などのモデル選択技術を使用して、最適なコンポーネントの数を選択することができます。

スペクトルクラスタリング

スペクトルクラスタリングは、グラフのラプラシアン行列のスペクトル特性を利用して、データのクラスタを特定するグラフベースのクラスタリング技術です。アルゴリズムは、各データポイントがノードであり、エッジの重みがデータポイント間のペアワイズの類似度を表す類似度グラフを構築することから始まります。その後、グラフラプラシアン行列を計算し、その固有ベクトルを使用して次元削減とクラスタリングを行います。

スペクトルクラスタリングは、非凸クラスタを検出するのに特に効果的であり、複雑な構造のデータを扱うのに適しています。ただし、大規模なデータセットの場合、ラプラシアン行列の固有分解により計算コストが高くなる場合があります。ニュストローム法やランダムアルゴリズムなどの様々な近似技術を使用して、スペクトルクラスタリングのスケーラビリティを向上させることができます。