PCAとは
主成分分析(PCA)は、データサイエンスの領域で広く用いられる技術であり、特に次元削減、データ可視化、ノイズ低減に用いられます。この強力な手法によって、研究者や実践者は大規模で複雑なデータセット内の隠れたパターンを分析し、有用な洞察を得て、意思決定の改善につなげることができます。
PCAのエッセンス
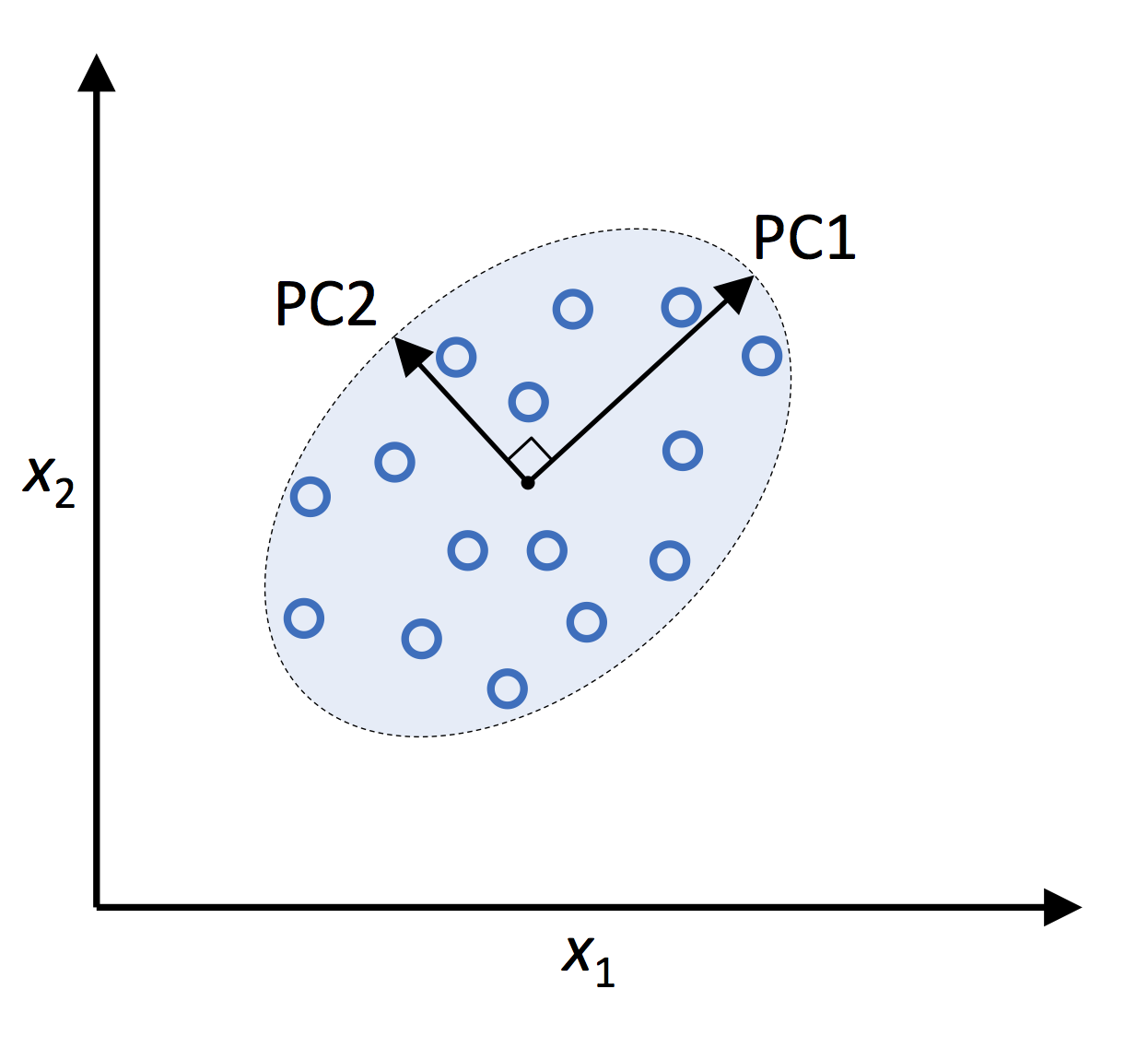
PCAの主な目的は、データセットの次元数を減らしながらできるだけ多くの情報を保持することです。これは、元の特徴量を新しい直交特徴量セット、すなわち主成分(PC)と呼ばれる線形結合に変換することで実現されます。主成分は分散の順にランク付けされ、最初の主成分がデータ内のもっとも多くの分散を説明し、次に2番目の主成分、そして以降に続きます。主成分のサブセットのみを保持することにより、データセットの次元数を効果的に削減し、重要な情報を失うことなく解析を簡素化することができます。
Python Machine Learning (2nd Ed.) Code Repository
PCAの数学的基礎
この章では、PCAの数学的基礎について掘り下げます。基礎的な線形代数と統計学の知識が必要です。
線形代数と固有値
PCAは、特に固有値と固有ベクトルに依存する線形代数の概念に基づいています。正方行列
ここで、
共分散行列
共分散行列は、データセット内の元の変数間の関係を捉えるためにPCAにおいて重要な要素です。
ここで、
固有値分解
固有値分解は、行列をその固有値と固有ベクトルに分解するプロセスです。PCAでは、共分散行列
次元削減
共分散行列の固有値と固有ベクトルを得たら、上位
ここで、
PCAの実践
この章では、公開されているデータセットである有名なアヤメデータセットを用いて、PCAをステップバイステップで実装します。このデータセットには、セトナアヤメ、バージニカアヤメ、ベルサヤノオアヤメの3種類の花に関する150サンプルが含まれており、次の4つの特徴量で構成されています。
- がく片の長さ
- がく片の幅
- 花弁の長さ
- 花弁の幅
次元削減を行いながら、データセットの固有構造を保持することが目的です。
データの前処理
PCAを実行する前に、データの前処理が必要です。主な前処理手順は、標準化です。標準化は、各特徴量を平均0、標準偏差1にスケーリングします。この手順がPCAが効果的に機能するためには必要です。
Pythonとscikit-learnライブラリを使用して、アヤメデータセットを前処理する方法を以下に示します。
import numpy as np
import pandas as pd
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
# Load the Iris dataset
iris = datasets.load_iris()
X = iris.data
# Standardize the data
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
PCAの実装
データが前処理されたので、scikit-learnライブラリを使用してPCAを実行できます。以下は、アヤメデータセットを2次元に削減するためのコードです。
from sklearn.decomposition import PCA
# Perform PCA with 2 components
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)
PCAの結果の解釈
PCAの出力は、次元が削減された新しいデータセット(X_pca)です。この例では、アヤメデータセットの次元を4から2に削減しました。各主成分の重要性を理解するために、各成分が説明する分散の割合を示す説明された分散比率を調べることができます。
explained_variance_ratio = pca.explained_variance_ratio_
print(explained_variance_ratio)
出力は、次のようになります。
array([0.72962445, 0.22850762])
これは、第1主成分がデータの総分散の約72.96%を説明し、第2主成分が約22.85%を説明していることを示しています。これら2つの成分を合わせると、総分散の約95.81%を説明します。
PCAコンポーネントの視覚化
最後に、散布図でPCA変換されたデータを視覚化することができます。これにより、次元削減されたデータセットのパターンやクラスターを観察することができます。以下は、matplotlibを使用して2つの主成分の散布図を作成するためのコードです。
import matplotlib.pyplot as plt
# Plot the PCA-transformed data
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=iris.target, cmap='viridis', edgecolor='k', s=75)
plt.xlabel('First Principal Component')
plt.ylabel('Second Principal Component')
plt.title('PCA with 2 Components on Iris Dataset')
plt.show()
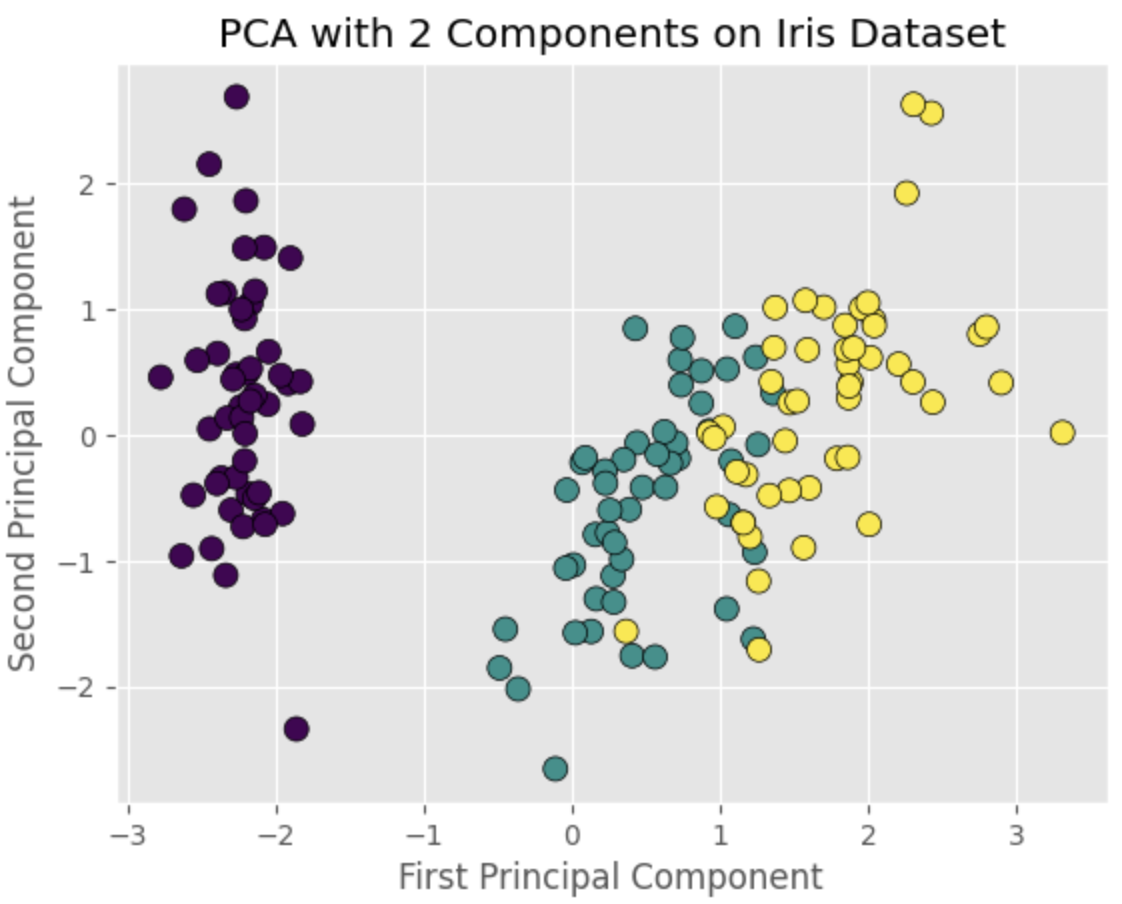
この散布図は、3種類のアヤメの種に対応する明確なクラスターを示しており、PCAがデータの次元を効果的に削減し、データの構造を維持できることを示しています。
主成分負荷量
主成分負荷量、または因子負荷量または固有ベクトル負荷量とも呼ばれるものは、各元の特徴量が特定の主成分にどのように貢献しているかを示す係数です。ローディングを分析することで、元の特徴量と主成分の間の関係、およびデータの基本的な構造を理解するのに役立ちます。
先に実装したPCAモデルを使用して、アヤメデータセットの主成分負荷量を取得する方法を以下に示します。
loadings = pca.components_
print(loadings)
出力は、次のようになります。
array([[ 0.52106591, -0.26934744, 0.5804131 , 0.56485654],
[ 0.37741762, 0.92329566, 0.02449161, 0.06694199]])
この配列は、2つの主成分負荷量を表し、各行が1つの主成分に対応し、各列が元の特徴量に対応しています。負荷量の絶対値が高いほど、対応する元の特徴量の貢献が強くなります。
例えば、最初の主成分では、花びらの長さ(0.580)と花びらの幅(0.565)のローディングが、がくの長さ(0.521)とがくの幅(-0.269)の負荷量よりも高いです。これは、最初の主成分が主に花びらの長さと花びらの幅の変動によって引き起こされることを示唆しています。
負荷量を視覚化するためには、バイプロットを作成することができます。バイプロットは、PCAに変換されたデータにオーバーレイされた負荷量を表すベクトルを含む散布図です。
def biplot(X_pca, loadings, labels=None):
plt.figure(figsize=(10, 7))
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=iris.target, cmap='viridis', edgecolor='k', s=75)
if labels is None:
labels = np.arange(loadings.shape[1])
for i, label in enumerate(labels):
plt.arrow(0, 0, loadings[0, i], loadings[1, i], color='r', alpha=0.8, lw=2)
plt.text(loadings[0, i] * 1.15, loadings[1, i] * 1.15, label, color='r', ha='center', va='center', fontsize=12)
plt.xlabel('First Principal Component')
plt.ylabel('Second Principal Component')
plt.title('PCA Biplot of Iris Dataset')
plt.grid()
plt.show()
feature_labels = iris.feature_names
biplot(X_pca, loadings, labels=feature_labels)
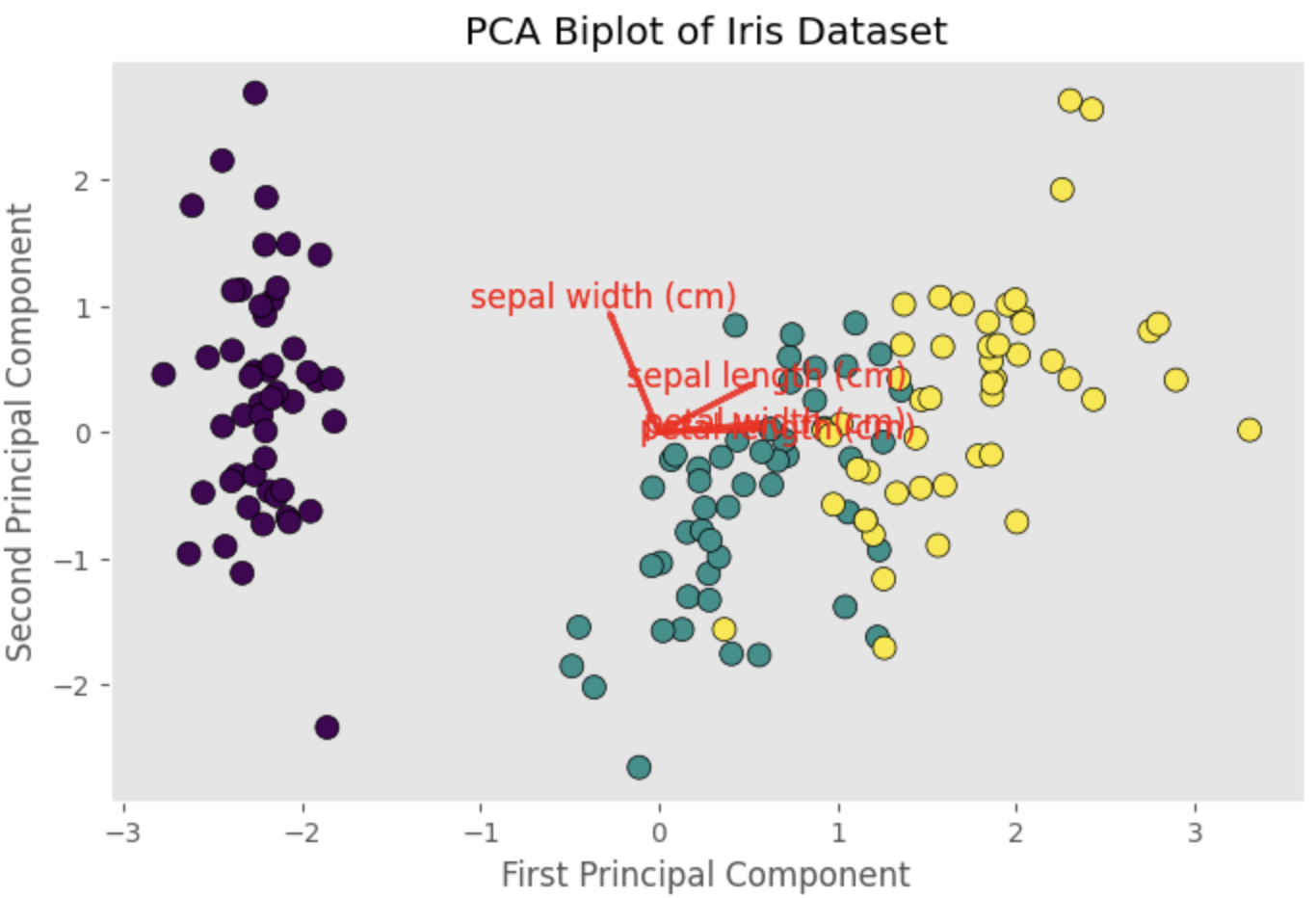
バイプロットには、がくの長さ、がくの幅、花びらの長さ、花びらの幅の負荷量を表すベクトルが表示されます。各ベクトルの方向と長さは、対応する特徴量が主成分にどの程度貢献しているかを示します。
参考