2022-03-29

相関係数

相関係数とは

相関係数は、2つの連続変数間の線形関係の強度と方向を数量化する数値的指標です。主な目的は、2つの変数がどの程度関連しているかを評価し、その関連の性質について洞察を提供することです。この章では、もっとも一般的に使用される2つの相関係数であるピアソン相関係数（ $r$ ）とスピアマン順位相関係数（ $\rho$ ）について詳しく説明します。

ピアソン相関係数

ピアソン相関係数（ $r$ ）は、次の式で計算されます。

r = \frac{\sum*{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum*{i=1}^{n}(x*i - \bar{x})^2 \sum*{i=1}^{n}(y_i - \bar{y})^2}}

ここで、

$n$ は対応するデータ点の数
$x_i$ と $y_i$ は個々のデータ点
$\bar{x}$ と $\bar{y}$ は、それぞれ $x$ および $y$ 変数の平均値

スピアマン順位相関係数

スピアマン順位相関係数（ $\rho$ ）は、次の式で計算されます。

\rho = 1 - \frac{6 \sum\_{i=1}^{n} d_i^2}{n(n^2 - 1)}

ここで、

$n$ は対応するデータ点の数
$d_i$ は、対応する $x_i$ および $y_i$ の値の順位の差

相関の解釈

相関係数の値は、-1から1までの範囲で表されます。相関の強度と方向性は次のように解釈できます。

-1 ≤ r < -0.7: 強い負の相関
-0.7 ≤ r < -0.3: 中程度の負の相関
-0.3 ≤ r < 0: 弱い負の相関
0: 相関がない
0 < r ≤ 0.3: 弱い正の相関
0.3 < r ≤ 0.7: 中程度の正の相関
0.7 < r ≤ 1: 強い正の相関

共分散と相関係数の関係

共分散と相関係数は、両方とも2つの変数間の関係性を測定する指標です。共分散は関係性の方向性（正の相関または負の相関）に関する情報を提供しますが、関係性の強度についての情報は提供しません。一方、相関係数は関係性の方向性だけでなく、-1から1の標準化されたスケールで関係性の強度も示します。

共分散とピアソン相関係数の関係は次の式で表されます。

r = \frac{cov(x, y)}{s_x s_y}

ここで、

$r$ はピアソン相関係数
$cov(x, y)$ は $x$ と $y$ の共分散
$s_x$ と $s_y$ は、それぞれ $x$ および $y$ の標準偏差

この式では、ピアソン相関係数は、2つの変数の標準偏差の積で割ることで共分散を標準化し、結果として得られる相関係数が-1から1の範囲に収まるようにしています。これにより、関係性の強度を解釈しやすくなります。

相関係数の制限と仮定

ピアソンの $r$ とスピアマンの $\rho$ には、値を解釈する際に考慮すべき特定の制限と仮定があります。

相関係数は、2つの変数間の線形関係の強度しか測定しないため、因果関係を意味しない
外れ値や極端な値は、相関係数に大きな影響を与えることがあり、誤った結果を導く可能性がある。データを散布図で視覚化して、外れ値を特定し、関係性の真の性質を評価することが重要です。
ピアソンの $r$ は、両方の変数が間隔尺度または比尺度で測定され、その関係が線形であることを前提としている。これらの仮定が満たされていない場合、結果が不正確になる可能性があります。
スピアマンの $\rho$ は、外れ値や非線形関係に対してより強いが、少なくとも1つの変数が順序尺度で測定されているか、関係性が単調である必要がある
相関係数はサンプルサイズに敏感であり、サンプルサイズが小さいと、強い関係が存在していても弱い相関が得られることがある。母集団を正確に表現するために、十分な大きさのサンプルサイズを確保することが重要です。

Pythonを使用した相関係数の計算

この章では、Pythonを使用して相関係数を計算する方法を示します。

まず、必要なライブラリをインポートします。

python

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

この例では、3つの変数（x、y、z）を含むサンプルデータセットを作成します。データを含むDataFrameを作成するためにpandasを使用します。

python

data = {
    'x': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
    'y': [2, 4, 6, 8, 10, 12, 14, 16, 18, 20],
    'z': [10, 9, 8, 7, 6, 5, 4, 3, 2, 1]
}

df = pd.DataFrame(data)

データセットの相関行列を計算するには、pandas DataFrameで利用可能なcorr()メソッドを使用できます。corr()メソッドでは、デフォルトでピアソン相関係数が使用されます。

correlation_matrix = df.corr()
print(correlation_matrix)

     x    y    z
x  1.0  1.0 -1.0
y  1.0  1.0 -1.0
z -1.0 -1.0  1.0

相関行列を視覚的に表示するために、seabornを使用してヒートマップを作成します。

python

plt.figure(figsize=(10, 7))
sns.set(font_scale=1.2)
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', annot_kws={"size": 12})
plt.title("Correlation Matrix")
plt.show()

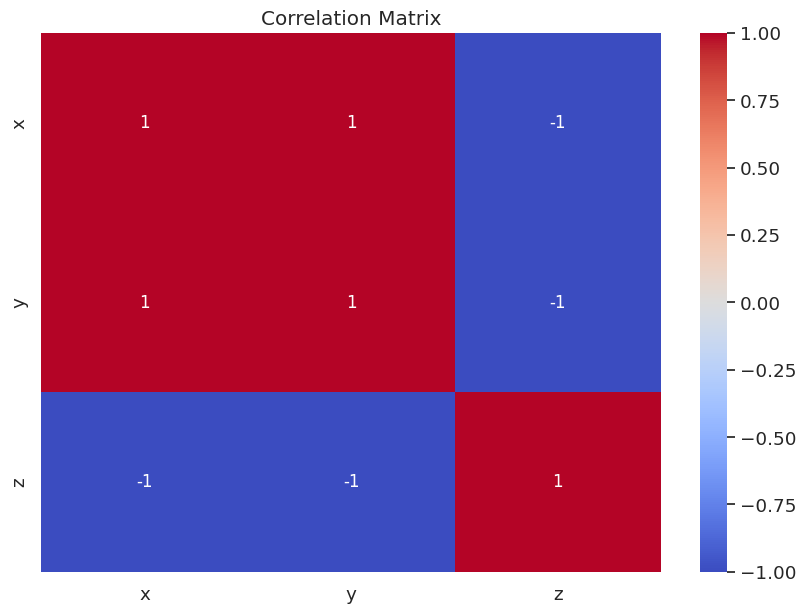
Correlation matrix

結果として得られた相関行列とヒートマップには、データセット内の各ペアの変数の相関係数が表示されます。

xとyの相関係数は1で、強い正の相関を示す
xとzの相関係数は-1で、強い負の相関を示す
yとzの相関係数も-1で、強い負の相関を示す

相関係数を解釈することで、データセット内の変数間の関係について洞察を得ることができます。この場合、xとyの間には強い正の線形関係があり、xとzおよびyとzの両方には強い負の線形関係があることがわかります。

相関の視覚的理解

相関係数が異なるデータを示すために、相関の度合いが異なる3つの異なるデータセットを生成し、各データセットの散布図を作成します。

python

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(42)

# Create dataset with a strong positive correlation
x1 = np.random.normal(50, 10, 100)
y1 = x1 * 1.2 + np.random.normal(0, 5, 100)

# Create dataset with a weak positive correlation
x2 = np.random.normal(50, 10, 100)
y2 = x2 * 0.2 + np.random.normal(0, 20, 100)

# Create dataset with no correlation
x3 = np.random.normal(50, 10, 100)
y3 = np.random.normal(50, 10, 100)

# Create scatterplots for each dataset
plt.figure(figsize=(18, 5))

plt.subplot(131)
plt.scatter(x1, y1)
plt.title("Strong Positive Correlation")
plt.xlabel("x1")
plt.ylabel("y1")

plt.subplot(132)
plt.scatter(x2, y2)
plt.title("Weak Positive Correlation")
plt.xlabel("x2")
plt.ylabel("y2")

plt.subplot(133)
plt.scatter(x3, y3)
plt.title("No Correlation")
plt.xlabel("x3")
plt.ylabel("y3")

plt.show()

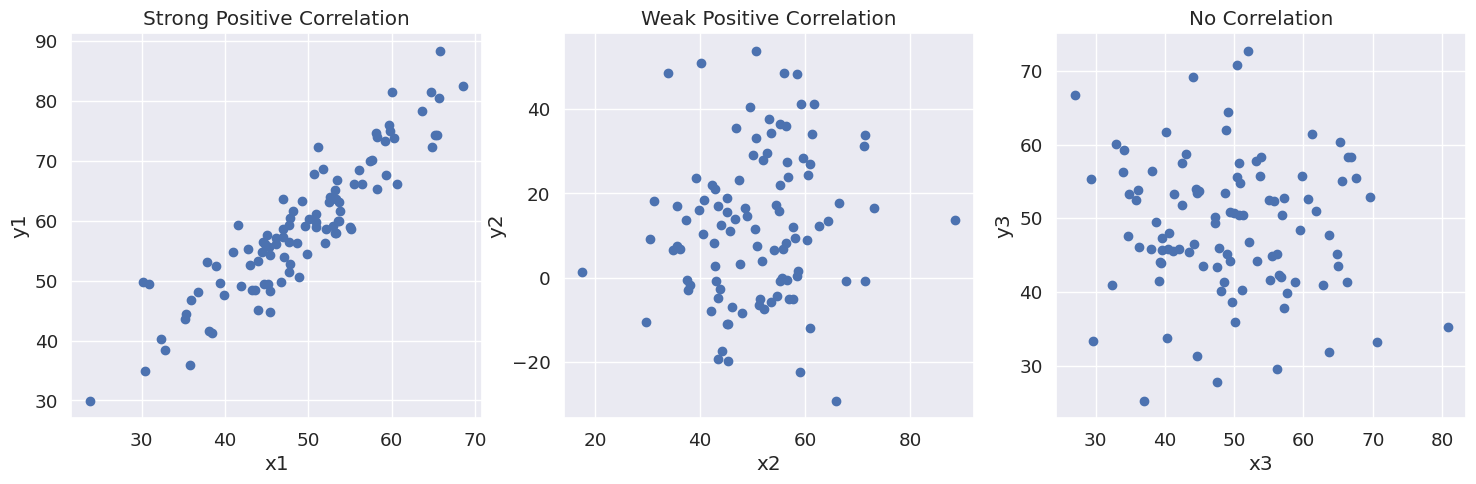
Correlation

上記のコードは、3つの異なるデータセットを生成します。

強い正の相関: このデータセットでは、x1とy1には強い正の線形関係があり、散布図では点が正の傾きの直線の周りに密集していることがわかります。
弱い正の相関: このデータセットでは、x2とy2には弱い正の線形関係があります。散布図は、点が正の傾きの直線の周りに散らばっていることを示していますが、強い正の相関の場合よりも散布が大きくなっています。
相関なし: このデータセットでは、x3とy3には線形関係がありません。散布図は、点がランダムに分布し、明確なパターンに従っていないことがわかります。