Pendahuluan

Ketika beberapa model statistik dibuat, artikel ini menjelaskan AIC, yang merupakan salah satu indikator model statistik mana yang dapat dianggap sebagai model yang baik.

Data dan Model

Dalam artikel ini, saya akan menggunakan data jumlah biji dan model statistik untuk 100 tanaman fiktif, yang diolah dalam artikel Model linier umum.

Datanya adalah sebagai berikut: y adalah jumlah biji per individu, x adalah ukuran individu, dan f adalah apakah individu tersebut telah diberi pupuk atau tidak (variabel kategorikal).

Dari data ini, model regresi Poisson berikut ini telah dibangun:

• Model statistik dimana jumlah benih tergantung pada ukuran (model x)
  • \lambda_i = e^{\beta_1 + \beta_2 x_i}
• Model statistik dimana jumlah benih tergantung pada ada atau tidaknya perlakuan pemupukan (model f)
  • \lambda_i = e^{\beta_1 + \beta_3 d_i} (d_i adalah variabel dummy)
• Model statistik di mana jumlah benih tergantung pada ukuran dan perlakuan pupuk (model xf)
  • \lambda_i = e^{\beta_1 + \beta_2 x_i + \beta_3 d_i} (d_i adalah variabel dummy)

Deviance

Kita telah mencari parameter yang memaksimalkan log-likelihood, yang merupakan goodness of fit terhadap data yang diamati, ketika parameter model statistik diestimasi dengan maximum likelihood.

Di sini, ada ukuran yang disebut deviance yang menunjukkan poor fit. Deviance D didefinisikan oleh persamaan berikut:

\log L^* adalah log-likelihood maksimum. Deviance yang sebenarnya hanyalah log-likelihood maksimum \log L^* dikalikan dengan -2.

Ringkasan hasil estimasi parameter untuk model x ditunjukkan di bawah ini.

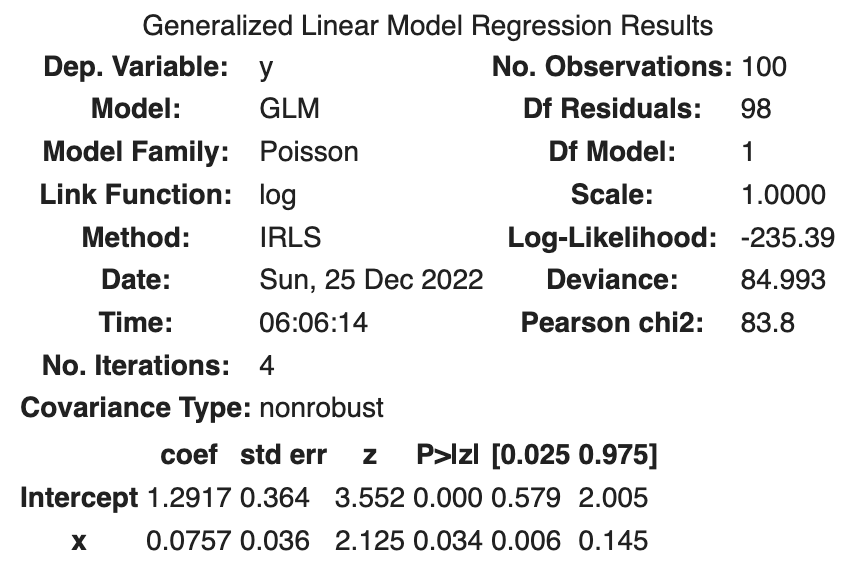
Log likelihood maksimum adalah -235.39, sehingga deviance D = \log L^*$ adalah 470.78. Akan tetapi, nilai 470.78 tidak ditampilkan dalam ringkasan, melainkan nilai Deviance yang ditampilkan.

Deviance yang ditampilkan adalah deviance residual, yang didefinisikan sebagai berikut.

D_{min} adalah deviasi dari model penuh. Model penuh adalah model yang dipasang dengan sejumlah parameter yang sesuai dengan jumlah data. Sebagai contoh, karena jumlah data dalam kasus ini adalah 100, maka model statistik yang dipasang dengan 100 parameter. Dengan kata lain, model penuh tidak bernilai sebagai model statistik karena hanya membaca semua data. Namun, model penuh memiliki goodness of fit maksimum, atau log-likelihood, dan deviance minimum D_{min}.

Deviance residual adalah nilai relatif dari fit yang buruk sehubungan dengan deviance dari model penuh.

Selanjutnya, kita mempertimbangkan deviasi residual maksimum. Model dengan deviasi maksimum adalah model dengan fit terburuk, yaitu model tanpa memasukkan variabel penjelas. Model ini disebut model Null.

Model Null dapat dikonstruksi sebagai berikut.

import statsmodels.api as sm
import statsmodels.formula.api as smf

fit_null = smf.glm('y ~ 1', data=df, family=sm.families.Poisson()).fit()
fit_null.summary()

Deviance residual maksimum D_{maks} adalah 89,507.

Tabel berikut ini merangkum penyimpangan-penyimpangan tersebut.

Berikut ini adalah ringkasan dari masing-masing model.

Dapat dilihat bahwa model dengan jumlah parameter yang lebih besar lebih cocok dengan data.

AIC

Kita telah melihat bahwa meningkatkan kompleksitas model, yaitu, meningkatkan jumlah parameter dalam model, meningkatkan log-likelihood maksimum dan meningkatkan kecocokan dengan data yang diamati. Namun, mungkin hanya cocok untuk data yang diamati yang diperoleh secara kebetulan, dan mungkin tidak cocok sama sekali untuk data lainnya. Dengan kata lain, mungkin bagus untuk satu set pengamatan, tetapi buruk untuk set pengamatan lainnya. Dalam istilah pembelajaran mesin, ini berarti Anda mungkin terlalu banyak berlatih pada data pelatihan.

AIC adalah ukuran yang menekankan prediksi yang baik daripada goodness of fit.

AIC dinyatakan dengan persamaan berikut:

k adalah jumlah parameter yang diestimasi dengan maximum likelihood. Semakin kecil AIC, semakin baik modelnya.

AIC dengan mudah dikeluarkan oleh kode berikut.

print('null model', fit_null.aic)
print('f model', fit_f.aic)
print('x model', fit_x.aic)

null model 477.2864426185736
f model 479.25451392137364
x model 477.2864426185736

Dengan menggunakan AIC sebagai kriteria, model x adalah model terbaik.

Catatan tentang pemilihan model dengan AIC

Jika data yang diamati sedikit, model dengan parameter yang lebih sedikit mungkin memiliki AIC yang lebih kecil daripada model yang sebenarnya. Model yang sederhana mungkin memiliki kekuatan prediksi yang lebih baik karena data yang diamati terlalu kecil untuk menemukan aturan praktis dalam data.