Apa itu analisis regresi?
Analisis regresi adalah teknik statistik yang mengekspresikan hubungan sebab-akibat sebagai fungsi dari faktor mana yang mempengaruhi hasil mana dan seberapa banyak. Dalam hal ini, nilai numerik yang merupakan hasil disebut variabel tujuan dan nilai numerik yang merupakan faktor disebut variabel penjelas.
Ketika hanya ada satu variabel penjelas, maka disebut analisis regresi sederhana, dan ketika ada beberapa variabel penjelas, maka disebut analisis regresi berganda.
Analisis regresi adalah teknik statistik yang banyak digunakan baik dalam bisnis maupun akademis.
Contoh-contoh analisis regresi
Berikut ini adalah contoh-contoh analisis regresi.
-
Prediksi harga real estate
- Analisis regresi Sederhana
- Variabel tujuan: harga real estat
- Variabel penjelas: ukuran lot
- Analisis regresi berganda
- Variabel tujuan: harga real estat
- Variabel penjelas: ukuran lot, jarak dari stasiun, usia bangunan, dll.
- Analisis regresi Sederhana
-
Prediksi tingkat klik pada iklan
- Analisis regresi sederhana
- Variabel tujuan: tingkat klik
- Variabel penjelas: judul
- Analisis regresi berganda
- Variabel objektif: rasio klik
- Variabel penjelas: judul, font, genre, dll.
- Analisis regresi sederhana
Analisis regresi dalam Python
Berikut adalah kode untuk mengimplementasikan analisis regresi dalam Python. Dalam hal ini, saya akan menggunakan data harga rumah Boston dari sklearn sebagai dataset.
import pandas as pd
from sklearn import datasets
boston = datasets.load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df["PRICE"] = boston.target
df.head()
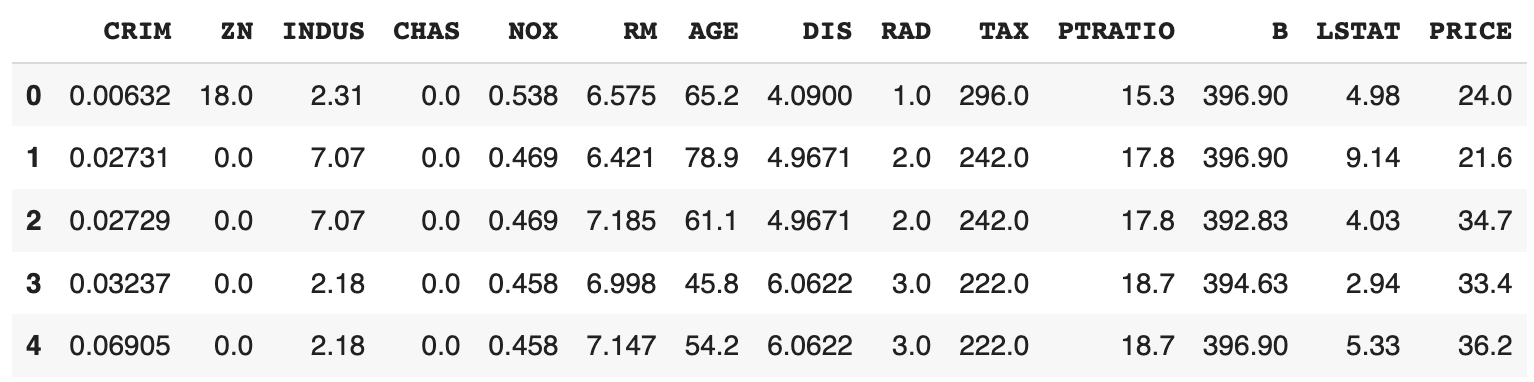
Label PRICE adalah harga rumah dan label lainnya adalah data karakteristik rumah.
Rincian dari label-label di setiap kolom dapat dilihat dengan DESCR.
print(boston.DESCR)
.. _boston_dataset:
Boston house prices dataset
---------------------------
**Data Set Characteristics:**
:Number of Instances: 506
:Number of Attributes: 13 numeric/categorical predictive. Median Value (attribute 14) is usually the target.
:Attribute Information (in order):
- CRIM per capita crime rate by town
- ZN proportion of residential land zoned for lots over 25,000 sq.ft.
- INDUS proportion of non-retail business acres per town
- CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
- NOX nitric oxides concentration (parts per 10 million)
- RM average number of rooms per dwelling
- AGE proportion of owner-occupied units built prior to 1940
- DIS weighted distances to five Boston employment centres
- RAD index of accessibility to radial highways
- TAX full-value property-tax rate per $10,000
- PTRATIO pupil-teacher ratio by town
- B 1000(Bk - 0.63)^2 where Bk is the proportion of black people by town
- LSTAT % lower status of the population
- MEDV Median value of owner-occupied homes in $1000's
:Missing Attribute Values: None
:Creator: Harrison, D. and Rubinfeld, D.L.
This is a copy of UCI ML housing dataset.
https://archive.ics.uci.edu/ml/machine-learning-databases/housing/
This dataset was taken from the StatLib library which is maintained at Carnegie Mellon University.
The Boston house-price data of Harrison, D. and Rubinfeld, D.L. 'Hedonic
prices and the demand for clean air', J. Environ. Economics & Management,
vol.5, 81-102, 1978. Used in Belsley, Kuh & Welsch, 'Regression diagnostics
...', Wiley, 1980. N.B. Various transformations are used in the table on
pages 244-261 of the latter.
The Boston house-price data has been used in many machine learning papers that address regression
problems.
.. topic:: References
- Belsley, Kuh & Welsch, 'Regression diagnostics: Identifying Influential Data and Sources of Collinearity', Wiley, 1980. 244-261.
- Quinlan,R. (1993). Combining Instance-Based and Model-Based Learning. In Proceedings on the Tenth International Conference of Machine Learning, 236-243, University of Massachusetts, Amherst. Morgan Kaufmann.
Pisahkan kumpulan data menjadi data pelatihan dan pengujian.
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(
boston.data,
boston.target,
random_state=0
)
Analisis regresi sederhana
Dalam analisis regresi sederhana, satu variabel penjelas memprediksi variabel tujuan. Dengan asumsi
Kita akan menggunakan sklearn python untuk menghitung RM dalam dataset sebagai variabel penjelas.
from sklearn import linear_model
x_rm_train = x_train[:, [5]]
x_rm_test = x_test[:, [5]]
model = linear_model.LinearRegression()
model.fit(x_train_rm, y_train)
a = model.coef_
b = model.intercept_
print("a: ", a)
print("b: ", b)
a: [9.31294923]
b: -36.180992646339206
Visualisasikan data dan model.
import matplotlib.pyplot as plt
plt.scatter(x_rm_train, y_train, label="Train")
plt.scatter(x_rm_test, y_test, label="Test")
y_pred = model.predict(x_rm_train)
plt.plot(x_rm_train, y_pred, c="black")
plt.xlabel("RM")
plt.ylabel("PRICE")
plt.legend()
plt.show()
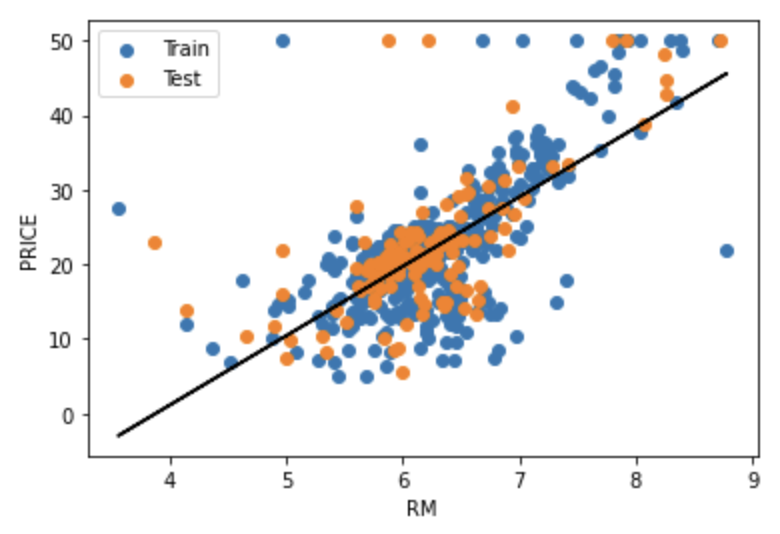
Train adalah data pelatihan, Test adalah data pengujian, dan garis hitam adalah model.
Koefisien determinasi
Menghitung koefisien determinasi
di mana
r2_score sklearn. Kode berikut menghitung
from sklearn.metrics import r2_score
y_pred_train = model.predict(x_rm_train)
print("R2 (train): ", r2_score(y_train, y_pred_train))
y_pred_test = model.predict(x_rm_test)
print("R2 (test): ", r2_score(y_test, y_pred_test))
R2 (train): 0.48752067939343646
R2 (test): 0.4679000543136781
MSE
Hitung Mean Squared Error (MSE) dari model, di mana
MSE yang lebih kecil dapat diinterpretasikan sebagai kesalahan yang lebih kecil dalam model.
Kode berikut ini menghitung MSE untuk data pelatihan dan data uji, masing-masing.
from sklearn.metrics import mean_squared_error
print("MSE (train): ", mean_squared_error(y_train, y_pred_train))
print("MSE (test): ", mean_squared_error(y_test, y_pred_test))
MSE (train): 43.71870658739849
MSE (test): 43.472041677202206
Analisis regresi berganda
Analisis regresi berganda memprediksi variabel tujuan dengan beberapa variabel penjelas. Model regresi berganda diwakili oleh persamaan berikut dengan
Kali ini, kita akan melakukan analisis regresi berganda dengan menggunakan semua variabel penjelas.
model = linear_model.LinearRegression()
model.fit(x_train, t_train)
a_df = pd.DataFrame(boston.feature_names, columns=["Exp"])
a_df["a"] = pd.Series(model.coef_)
a_df
| Exp | a | |
|---|---|---|
| 0 | CRIM | -0.117735 |
| 1 | ZN | 0.044017 |
| 2 | INDUS | -0.005768 |
| 3 | CHAS | 2.393416 |
| 4 | NOX | -15.589421 |
| 5 | RM | 3.768968 |
| 6 | AGE | -0.007035 |
| 7 | DIS | -1.434956 |
| 8 | RAD | 0.240081 |
| 9 | TAX | -0.011297 |
| 10 | PTRATIO | -0.985547 |
| 11 | B | 0.008444 |
| 12 | LSTAT | -0.499117 |
print("b: ", model.intercept_)
b: 36.93325545712031
Koefisien determinasi
Hitung koefisien determinasi untuk masing-masing data pelatihan dan data uji.
from sklearn.metrics import r2_score
y_pred_train = model.predict(x_rm_train)
print("R2 (train): ", r2_score(y_train, y_pred_train))
y_pred_test = model.predict(x_rm_test)
print("R2 (test): ", r2_score(y_test, y_pred_test))
R2 (train): 0.7697699488741149
R2 (test): 0.635463843320211
Dibandingkan dengan model regresi sederhana,
MSE
Hitung MSE pada masing-masing data pelatihan dan pengujian.
from sklearn.metrics import mean_squared_error
print("MSE (train): ", mean_squared_error(y_train, y_pred_train))
print("MSE (test): ", mean_squared_error(y_test, y_pred_test))
MSE (train): 19.640519427908046
MSE (test): 29.78224509230252
MSE lebih kecil dibandingkan dengan model regresi sederhana. Namun, MSE untuk data uji secara signifikan lebih besar daripada MSE untuk data pelatihan. Dengan kata lain, model ini mungkin telah over-fitted terhadap data training. Dengan demikian, kebaikan model harus dinilai tidak hanya dalam hal peningkatan
Referensi
/ja/articles/loss-functon