What is geometric distribution

A geometric distribution is a probability distribution that follows a probability p of an event occurring the number of times until that event occurs. The geometric distribution is used in the following example.

• The number of times a coin is tossed until the front comes up
• Number of shots a basketball player with a 30% three-point success rate takes before making a three-pointer

When the random variable X follows a geometric distribution, the probability of an event occurring for the first time at the kth time in a trial with probability p of occurrence is expressed as follows:

The geometric distribution is sometimes denoted as X \sim Geo(p).

For p = 0.05, 0.1, and 0.5, the geometric distribution is as follows.

For example, the probability that the third toss of a coin will produce a face for the first time can be determined as follows:

We found that the probability of the table appearing for the first time on the third throw is 12.5%.

Relationship to binomial distribution

The binomial distribution is a probability distribution that follows the number of times an event occurs when p is the probability of an event occurring and n observations of that event are made. A geometric distribution, on the other hand, is a probability distribution that follows the number of times an event occurs when p is the probability of the event occurring.

In other words, the binomial distribution considers the same event in terms of "number of times" while the geometric distribution considers it in terms of "time/interval.

We can also say that the geometric distribution is the value of n when X_1=X_2=...=X_{n-1}=0, X_n=1 in a random variable X_1,X_2,..., that follows a Bernoulli distribution with probability p.

Expected value and variance of geometric distribution

When a random variable X follows a geometric distribution with probability of success p, its expected value and variance are as follows:

Memoryless of geometric distribution

If the random variable X follows a geometric distribution and m, n > 0, then the following equation holds.

The above equation implies that the time until the occurrence of a future event does not depend on the existence of that past event. For example, if a coin is tossed three times, and the first two tosses are all true, the result does not affect the probability of the third toss being true at all. This property is called memoryless. The geometric distribution is the only discrete distribution with memoryless.

Python Code

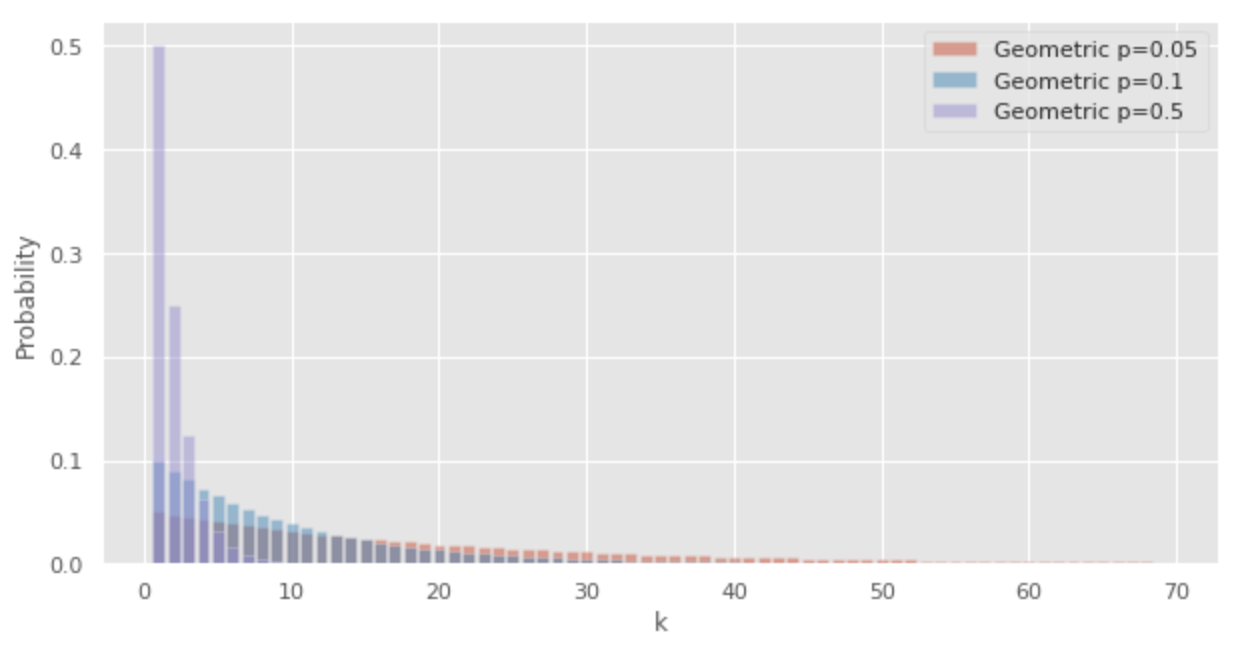
The following Python code can be used to draw geometric distributions.

import numpy as np
from scipy.stats import geom
import matplotlib.pyplot as plt

x =  np.arange(1, 70, 1)

# probability of the geometric distribution
y005= [geom.pmf(i, 0.05) for i in x]
y01= [geom.pmf(i, 0.1) for i in x]
y05= [geom.pmf(i, 0.5) for i in x]

# draw graph
plt.style.use('ggplot')
fig, ax = plt.subplots(facecolor="w", figsize=(10, 5))

ax.bar(x,y005,alpha=0.5, label="Geometric p=0.05")
ax.bar(x,y01,alpha=0.5, label="Geometric p=0.1")
ax.bar(x,y05,alpha=0.5, label="Geometric p=0.5")

ax.legend()
ax.set_xlabel("k")
ax.set_ylabel("Probability")
plt.show()