What is the categorical distribution

A categorical distribution is a probability distribution that the random variable X follows when K events X_1, X_2, ..., X_K are obtained with probability p_1, p_2, ..., p_K each in one trial.

The categorical distribution is a probability distribution that extends the Bernoulli distribution to the K dimension. In the Bernoulli distribution, there are two events (K=2), but when the number of events is six (K=6), such as the number of dice rolls, i.e., multi-dimensional, it becomes a categorical distribution.

The probability of the categorical distribution is expressed by the following equation:

Categorical distribution is sometimes denoted as Categorical(p).

Expected value and variance of categorical distribution

The expected value and variance of the categorical distribution are respectively:

Check categorical distributions with Python

Let's check the categorical distribution with Python.

First, consider the example of dice (K=6). We will perform 6000 trials with \frac{1}{6} as the probability of each dice roll. The following is the Python code.

import numpy as np
import matplotlib.pyplot as plt

plt.style.use('ggplot')
fig, ax = plt.subplots(facecolor="w", figsize=(10, 5))

p = [1/6, 1/6, 1/6, 1/6, 1/6, 1/6]

data = np.random.choice([1,2,3,4,5,6], p=p, size=6000)
plt.hist(data, bins = [0.5 + v for v in range(len(p) + 1)], alpha=0.5)

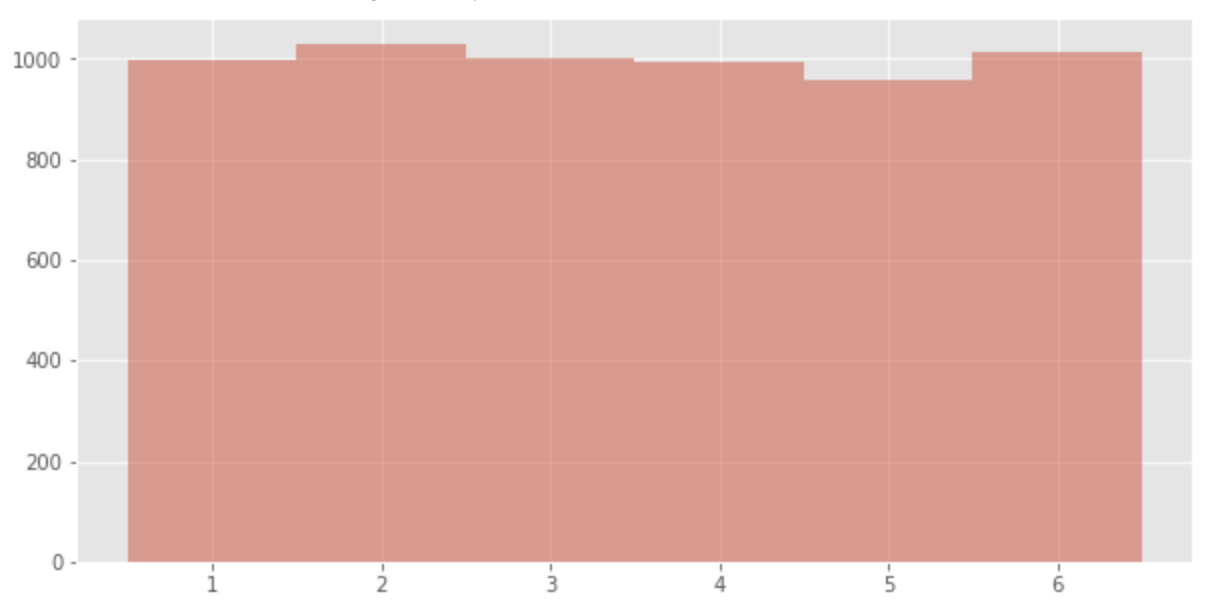
We can see that the number of occurrences of any eye is about 1000.

Next, suppose we have K=4 events, each with probabilities \frac{2}{10}, \frac{1}{10}, \frac{5}{10}, and \frac{2}{10}. Observe this event 10000 times. How about the Python code.

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import MaxNLocator

plt.style.use('ggplot')
fig, ax = plt.subplots(facecolor="w", figsize=(10, 5))
ax.xaxis.set_major_locator(MaxNLocator(integer=True))

p = [2/10, 1/10, 5/10, 2/10]

data = np.random.choice([1,2,3,4], p=p, size=10000)
plt.hist(data, bins = [0.5 + v for v in range(len(p) + 1)], alpha=0.5)

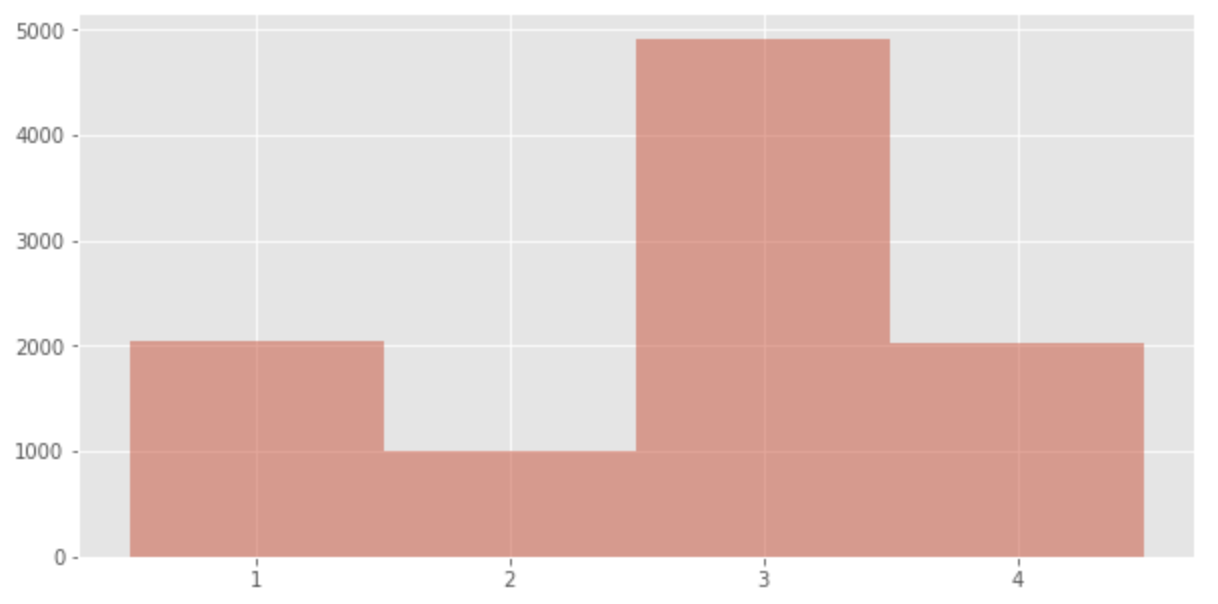
We can see that the distribution is in line with the probability.