What is Poisson distribution

Poisson distribution is a probability distribution that is followed by the probability of an event occurring k times, with an average of \lambda times per unit time (period). The Poisson distribution is often applied to real-world problems. For example

• Probability of 10 people per hour visiting a restaurant that serves 1 person per hour
• Probability that an intersection with an average of 3 traffic accidents per day will have no traffic accidents today

When the random variable X follows a Poisson distribution, the probability that an event that occurs on average \lambda times in a given period occurs k times can be found by the following equation.

From the above equation, we see that the Poisson distribution depends only on \lambda. For \lambda of 1, 10, 20, and 50, the distribution is as follows.

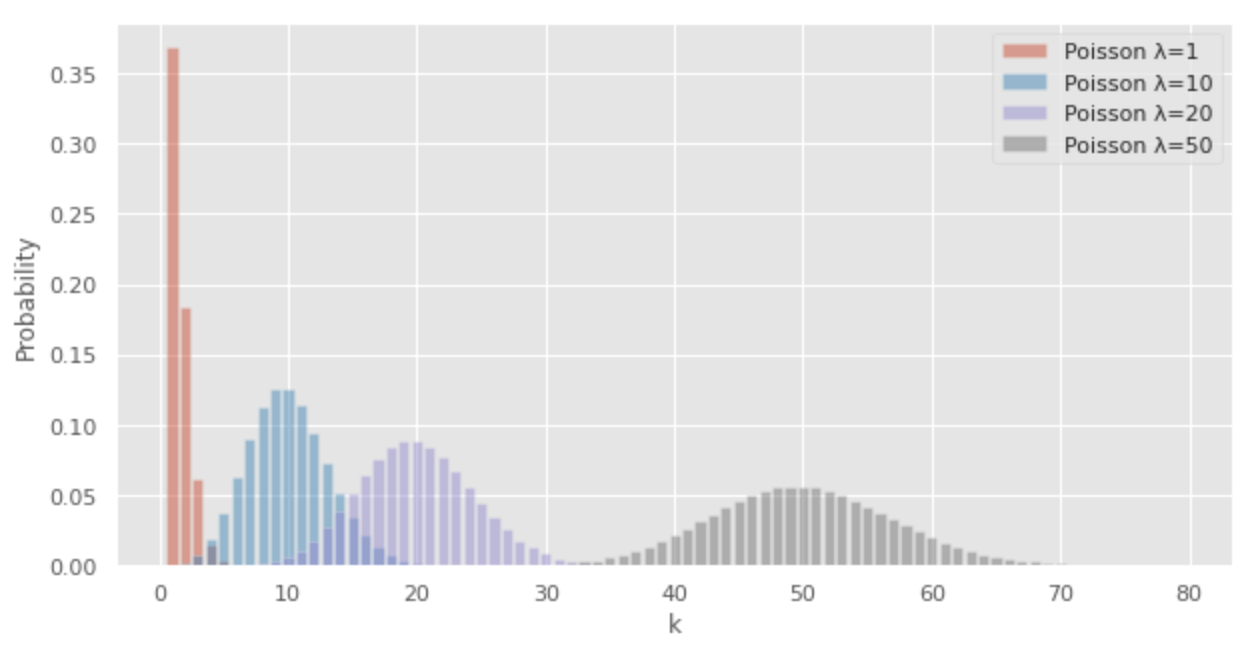
The larger \lambda is, the closer the distribution approaches a normal distribution.

As an example of probability calculation for the Poisson distribution, let us find the probability of 10 customers per hour at a restaurant that serves an average of 5 customers per hour. In this case, \lambda=5 and k=10. Calculate the probabilities as follows.

The probability of 10 visitors per hour was 1.8%.

Relationship with binomial distribution

The binomial distribution is a probability distribution that the number of times X that an event actually occurs for a given number of trials with probability n as p. The Poisson distribution can be expressed in the limit of n \to \infty and p \to 0, with the binomial distribution np constant as the constant \lambda.

From the above equation, to assume that an event follows a Poisson distribution, we need to deal with small values of probability p, i.e., events that occur infrequently. For this reason, the Poisson distribution often uses a unit of time that can be infinitely delimited.

The probability of a traffic accident occurring in one second is infinitesimally small. In this way, time can be infinitely small and the probability p can be as close to 0 as possible, which is why the Poisson distribution is often applied.

Expected value and variance of Poisson distribution

The expectation and variance of the Poisson distribution are both \lambda.

Reproductive property of the Poisson distribution

Suppose that the random variables X and Y are independent of each other according to the Poisson distribution, respectively, as follows.

In this case, from the reproductive property of the Poisson distribution, X + Y follows the Poisson distribution below.

Python Code

The following Python code can be used to draw a Poisson distribution.

import numpy as np
from scipy.stats import poisson
import matplotlib.pyplot as plt

x =  np.arange(1, 80, 1)

# probability of the poisson distribution
y1= [poisson.pmf(i, 1) for i in x]
y10= [poisson.pmf(i, 10) for i in x]
y20= [poisson.pmf(i, 20) for i in x]
y50= [poisson.pmf(i, 50) for i in x]

# draw graph
plt.style.use('ggplot')
fig, ax = plt.subplots(facecolor="w", figsize=(10, 5))
# plt.grid()

ax.bar(x,y1,alpha=0.5, label="Poisson λ=1")
ax.bar(x,y10,alpha=0.5, label="Poisson λ=10")
ax.bar(x,y20,alpha=0.5, label="Poisson λ=20")
ax.bar(x,y50,alpha=0.5, label="Poisson λ=50")

ax.legend()
ax.set_xlabel("k")
ax.set_ylabel("Probability")
plt.show()