2023-02-17

言語処理100本ノック第8章：ニューラルネット

Machine Learning

NLP

はじめに

言語処理100本ノックというNLPに関する問題集が東京工業大学によって作成、管理されています。

https://nlp100.github.io/ja/ch08.html

この記事では、「第8章: ニューラルネット」について回答例を紹介します。

70. 単語ベクトルの和による特徴量

問題 50 で構築した学習データ，検証データ，評価データを行列・ベクトルに変換したい．例えば，学習データについて，すべての事例 $x_i$ の特徴ベクトル $\boldsymbol{x}_i$ を並べた行列 $X$ と正解ラベルを並べた行列（ベクトル） $Y$ を作成したい．

X = \begin{pmatrix} \boldsymbol{x}_1 \\ \boldsymbol{x}_2 \\ \dots \\ \boldsymbol{x}_n \\ \end{pmatrix} \in \mathbb{R}^{n \times d}, Y = \begin{pmatrix} y_1 \\ y_2 \\ \dots \\ y_n \\ \end{pmatrix} \in \mathbb{N}^{n}

ここで， $n$ は学習データの事例数であり， $\boldsymbol x_i \in \mathbb{R}^d$ と $y_i \in \mathbb N$ はそれぞれ， $i \in \{1, \dots, n\}$ 番目の事例の特徴量ベクトルと正解ラベルを表す．
なお，今回は「ビジネス」「科学技術」「エンターテイメント」「健康」の 4 カテゴリ分類である． $\mathbb N_{<4}$ で $4$ 未満の自然数（ $0$ を含む）を表すことにすれば，任意の事例の正解ラベル $y_i$ は $y_i \in \mathbb N_{<4}$ で表現できる．
以降では，ラベルの種類数を $L$ で表す（今回の分類タスクでは $L=4$ である）．

$i$ 番目の事例の特徴ベクトル $\boldsymbol x_i$ は，次式で求める．

\boldsymbol x_i = \frac{1}{T_i} \sum_{t=1}^{T_i} \mathrm{emb}(w_{i,t})

ここで， $i$ 番目の事例は $T_i$ 個の（記事見出しの）単語列 $(w_{i,1}, w_{i,2}, \dots, w_{i,T_i})$ から構成され， $\mathrm{emb}(w) \in \mathbb{R}^d$ は単語 $w$ に対応する単語ベクトル（次元数は $d$ ）である．すなわち， $i$ 番目の事例の記事見出しを，その見出しに含まれる単語のベクトルの平均で表現したものが $\boldsymbol x_i$ である．今回は単語ベクトルとして，問題 60 でダウンロードしたものを用いればよい． $300$ 次元の単語ベクトルを用いたので， $d=300$ である．
$i$ 番目の事例のラベル $y_i$ は，次のように定義する．

y_i = \begin{cases} 0 & (\textrm{記事}\boldsymbol x_i\textrm{が「ビジネス」カテゴリの場合}) \\ 1 & (\textrm{記事}\boldsymbol x_i\textrm{が「科学技術」カテゴリの場合}) \\ 2 & (\textrm{記事}\boldsymbol x_i\textrm{が「エンターテイメント」カテゴリの場合}) \\ 3 & (\textrm{記事}\boldsymbol x_i\textrm{が「健康」カテゴリの場合}) \\ \end{cases}

なお，カテゴリ名とラベルの番号が一対一で対応付いていれば，上式の通りの対応付けでなくてもよい．

以上の仕様に基づき，以下の行列・ベクトルを作成し，ファイルに保存せよ．

学習データの特徴量行列: $X_{\rm train} \in \mathbb{R}^{N_t \times d}$

学習データのラベルベクトル: $Y_{\rm train} \in \mathbb{N}^{N_t}$

検証データの特徴量行列: $X_{\rm valid} \in \mathbb{R}^{N_v \times d}$

検証データのラベルベクトル: $Y_{\rm valid} \in \mathbb{N}^{N_v}$

評価データの特徴量行列: $X_{\rm test} \in \mathbb{R}^{N_e \times d}$

評価データのラベルベクトル: $Y_{\rm test} \in \mathbb{N}^{N_e}$

なお， $N_t, N_v, N_e$ はそれぞれ，学習データの事例数，検証データの事例数，評価データの事例数である．

!wget https://archive.ics.uci.edu/ml/machine-learning-databases/00359/NewsAggregatorDataset.zip
!unzip NewsAggregatorDataset.zip

import pandas as pd
from sklearn.model_selection import train_test_split
from gensim.models import KeyedVectors
import string
import torch

df = pd.read_csv('./newsCorporay.csv',
                 header=None,
                 sep='\t',
                 names=['ID', 'TITLE', 'URL', 'PUBLISHER', 'CATEGORY', 'STORY', 'HOSTNAME', 'TIMESTAMP']
                 )

df = df.loc[df['PUBLISHER'].isin(['Reuters', 'Huffington Post', 'Businessweek', 'Contactmusic.com', 'Daily Mail']), ['TITLE', 'CATEGORY']]

# split data
train, valid_test = train_test_split(
    df,
    test_size=0.2,
    shuffle=True,
    random_state=42,
    stratify=df['CATEGORY']
)
valid, test = train_test_split(
    valid_test,
    test_size=0.5,
    shuffle=True,
    random_state=42,
    stratify=valid_test['CATEGORY']
)

model = KeyedVectors.load_word2vec_format('GoogleNews-vectors-negative300.bin.gz', binary=True)

def w2v(text):
  words = text.translate(str.maketrans(string.punctuation, ' '*len(string.punctuation))).split()
  vec = [model[word] for word in words if word in model]
  return torch.tensor(sum(vec) / len(vec))

# create x vectors
X_train = torch.stack([w2v(text) for text in train['TITLE']])
X_valid = torch.stack([w2v(text) for text in valid['TITLE']])
X_test = torch.stack([w2v(text) for text in test['TITLE']])

# create y vectors
category_dict = {'b': 0, 't': 1, 'e':2, 'm':3}
y_train = torch.tensor(train['CATEGORY'].map(lambda x: category_dict[x]).values)
y_valid = torch.tensor(valid['CATEGORY'].map(lambda x: category_dict[x]).values)
y_test = torch.tensor(test['CATEGORY'].map(lambda x: category_dict[x]).values)

# save
torch.save(X_train, 'X_train.pt')
torch.save(X_valid, 'X_valid.pt')
torch.save(X_test, 'X_test.pt')
torch.save(y_train, 'y_train.pt')
torch.save(y_valid, 'y_valid.pt')
torch.save(y_test, 'y_test.pt')

71. 単層ニューラルネットワークによる予測

問題 70 で保存した行列を読み込み，学習データについて以下の計算を実行せよ．

\hat{y}_1=softmax(x_1W),\\\hat{Y}=softmax(X_{[1:4]}W)

ただし， $softmax$ はソフトマックス関数， $X_{[1:4]}∈\mathbb{R}^{4×d}$ は特徴ベクトル $x_1$ , $x_2$ , $x_3$ , $x_4$ を縦に並べた行列である．

X_{[1:4]}=\begin{pmatrix}x_1\\x_2\\x_3\\x_4\end{pmatrix}

行列 $W \in \mathbb{R}^{d \times L}$ は単層ニューラルネットワークの重み行列で，ここではランダムな値で初期化すればよい（問題 73 以降で学習して求める）．なお， $\hat{\boldsymbol y_1} \in \mathbb{R}^L$ は未学習の行列 $W$ で事例 $x_1$ を分類したときに，各カテゴリに属する確率を表すベクトルである．
同様に， $\hat{Y} \in \mathbb{R}^{n \times L}$ は，学習データの事例 $x_1, x_2, x_3, x_4$ について，各カテゴリに属する確率を行列として表現している．

from torch import nn

class SimpleNet(nn.Module):
  def __init__(self, input_size, output_size):
    super().__init__()
    self.fc = nn.Linear(input_size, output_size, bias=False)
    nn.init.normal_(self.fc.weight, 0.0, 1.0)

  def forward(self, x):
    x = self.fc(x)
    return x

model = SimpleNet(300, 4)

y1_hat = torch.softmax(model(X_train[0]), dim=-1)
print(y1_hat)
print('\n')
Y_hat = torch.softmax(model.forward(X_train[:4]), dim=-1)
print(Y_hat)


>> tensor([0.6961, 0.0492, 0.0851, 0.1696], grad_fn=<SoftmaxBackward0>)
>>
>> tensor([[0.6961, 0.0492, 0.0851, 0.1696],
>>         [0.5393, 0.0273, 0.3510, 0.0824],
>>         [0.7999, 0.0519, 0.1301, 0.0182],
>>         [0.3292, 0.1503, 0.1286, 0.3919]], grad_fn=<SoftmaxBackward0>)

72. 損失と勾配の計算

学習データの事例 $x_1$ と事例集合 $x_1$ , $x_2$ , $x_3$ , $x_4$ に対して，クロスエントロピー損失と，行列 $W$ に対する勾配を計算せよ．なお，ある事例 $x_i$ に対して損失は次式で計算される．

l_i=-log[事例x_iがy_iに分類される確率]

ただし，事例集合に対するクロスエントロピー損失は，その集合に含まれる各事例の損失の平均とする．

criterion = nn.CrossEntropyLoss()

loss_1 = criterion(model(X_train[0]), y_train[0])
model.zero_grad()
loss_1.backward()
print(f'loss: {loss_1:.3f}')
print(f'gradient:\n{model.fc.weight.grad}')

loss = criterion(model(X_train[:4]), y_train[:4])
model.zero_grad()
loss.backward()
print(f'loss: {loss:.3f}')
print(f'gradient:\n{model.fc.weight.grad}')

>>loss: 2.074
>>gradient:
>>tensor([[ 0.0010,  0.0071,  0.0020,  ..., -0.0181,  0.0040,  0.0138],
>>        [ 0.0010,  0.0073,  0.0021,  ..., -0.0185,  0.0041,  0.0141],
>>        [-0.0075, -0.0549, -0.0157,  ...,  0.1400, -0.0308, -0.1068],
>>        [ 0.0055,  0.0406,  0.0116,  ..., -0.1034,  0.0228,  0.0789]])
>>
>>loss: 2.796
>>gradient:
>>tensor([[ 0.0241, -0.0344, -0.0255,  ..., -0.0221, -0.0253, -0.0218],
>>        [-0.0181,  0.0021,  0.0147,  ..., -0.0224, -0.0172,  0.0403],
>>        [-0.0018, -0.0030, -0.0008,  ...,  0.0443,  0.0063, -0.0327],
>>        [-0.0042,  0.0352,  0.0116,  ...,  0.0002,  0.0363,  0.0143]])

73. 確率的勾配降下法による学習

確率的勾配降下法（SGD: Stochastic Gradient Descent）を用いて，行列 $W$ を学習せよ．なお，学習は適当な基準で終了させればよい（例えば「100 エポックで終了」など）．

class Dataset(torch.utils.data.Dataset):
  def __init__(self, X, y):
    self.X = X
    self.y = y
    self.size = len(y)

  def __len__(self):
    return self.size

  def __getitem__(self, index):
    return [self.X[index], self.y[index]]

# create Dataset
train_ds = Dataset(X_train, y_train)
valid_ds = Dataset(X_valid, y_valid)
test_ds = Dataset(X_test, y_test)

# create Dataloader
train_dl = torch.utils.data.DataLoader(train_ds,
                                       batch_size=1,
                                       shuffle=True
                                       )
valid_dl = torch.utils.data.DataLoader(valid_ds,
                                       batch_size=len(valid_ds),
                                       shuffle=False
                                       )
test_dl = torch.utils.data.DataLoader(test_ds,
                                      batch_size=len(test_ds),
                                      shuffle=False
                                      )

model = SimpleNet(300, 4)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)

num_epochs = 10
for epoch in range(num_epochs):
  model.train()
  loss_train = 0.0
  for i, (inputs, labels) in enumerate(train_dl):
    optimizer.zero_grad()
    outputs = model(inputs)
    loss = criterion(outputs, labels)
    loss.backward()
    optimizer.step()
    loss_train += loss.item()

  loss_train = loss_train / i
  model.eval()
  with torch.no_grad():
    inputs, labels = next(iter(valid_dl))
    outputs = model(inputs)
    loss_valid = criterion(outputs, labels)

  print(f'epoch: {epoch + 1}, loss_train: {loss_train:.3f}, loss_valid: {loss_valid:.3f}')

>> epoch: 1, loss_train: 0.471, loss_valid: 0.367
>> epoch: 2, loss_train: 0.309, loss_valid: 0.335
>> epoch: 3, loss_train: 0.281, loss_valid: 0.320
>> epoch: 4, loss_train: 0.265, loss_valid: 0.314
>> epoch: 5, loss_train: 0.256, loss_valid: 0.307
>> epoch: 6, loss_train: 0.250, loss_valid: 0.308
>> epoch: 7, loss_train: 0.244, loss_valid: 0.304
>> epoch: 8, loss_train: 0.240, loss_valid: 0.305
>> epoch: 9, loss_train: 0.237, loss_valid: 0.303
>> epoch: 10, loss_train: 0.234, loss_valid: 0.305

74. 正解率の計測

問題 73 で求めた行列を用いて学習データおよび評価データの事例を分類したとき，その正解率をそれぞれ求めよ．

def calc_accuracy(model, loader):
  model.eval()
  total = 0
  correct = 0
  with torch.no_grad():
    for inputs, labels in loader:
      outputs = model(inputs)
      pred = torch.argmax(outputs, dim=-1)
      total += len(inputs)
      correct += (pred == labels).sum().item()
  return correct / total

acc_train = calc_accuracy(model, train_dl)
acc_test = calc_accuracy(model, test_dl)
print(f'accuracy (train)：{acc_train:.3f}')
print(f'accuracy (test)：{acc_test:.3f}')

>> accuracy (train)：0.923
>> accuracy (test)：0.900

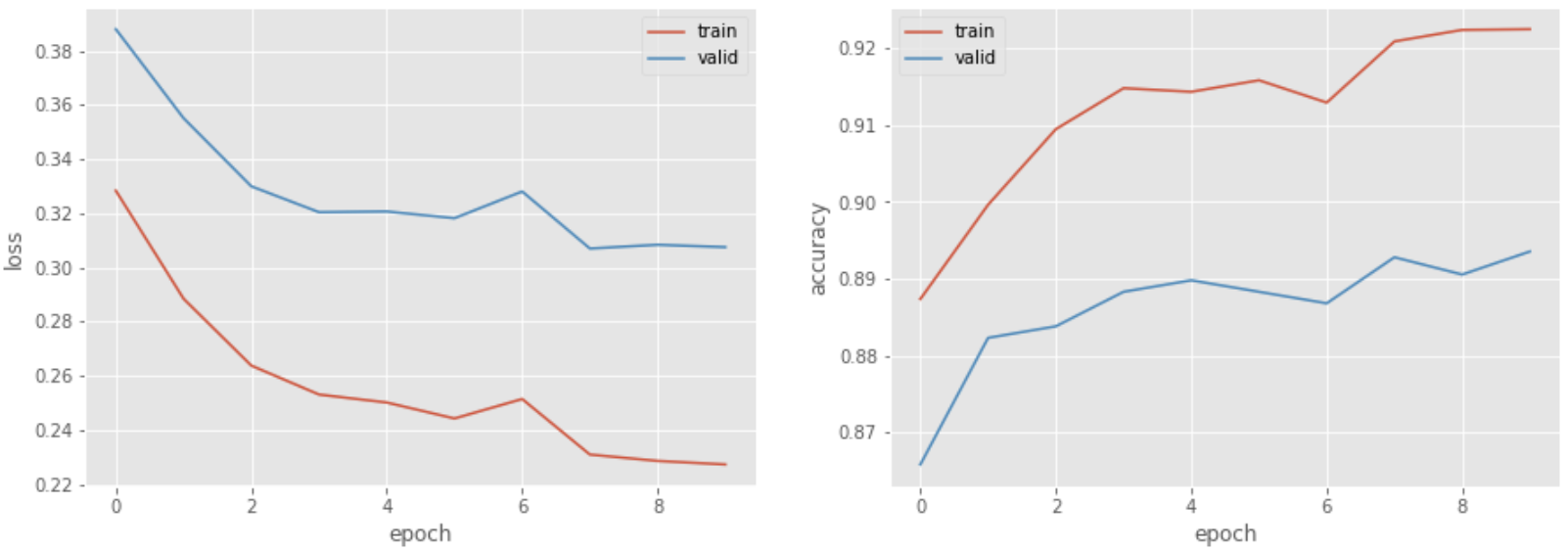
75. 損失と正解率のプロット

問題 73 のコードを改変し，各エポックのパラメータ更新が完了するたびに，訓練データでの損失，正解率，検証データでの損失，正解率をグラフにプロットし，学習の進捗状況を確認できるようにせよ．

def calc_loss_and_accuracy(model, criterion, loader):
  model.eval()
  loss = 0.0
  total = 0
  correct = 0
  with torch.no_grad():
    for inputs, labels in loader:
      outputs = model(inputs)
      loss += criterion(outputs, labels).item()
      pred = torch.argmax(outputs, dim=-1)
      total += len(inputs)
      correct += (pred == labels).sum().item()
  return loss / len(loader), correct / total

model = SimpleNet(300, 4)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)

num_epochs = 10
log_train = []
log_valid = []
for epoch in range(num_epochs):
  model.train()
  for inputs, labels in train_dl:
    optimizer.zero_grad()
    outputs = model(inputs)
    loss = criterion(outputs, labels)
    loss.backward()
    optimizer.step()

  loss_train, acc_train = calc_loss_and_accuracy(model, criterion, train_dl)
  loss_valid, acc_valid = calc_loss_and_accuracy(model, criterion, valid_dl)
  log_train.append([loss_train, acc_train])
  log_valid.append([loss_valid, acc_valid])

from matplotlib import pyplot as plt
import numpy as np

plt.style.use('ggplot')

fig, ax = plt.subplots(1, 2, figsize=(15, 5))
ax[0].plot(np.array(log_train).T[0], label='train')
ax[0].plot(np.array(log_valid).T[0], label='valid')
ax[0].set_xlabel('epoch')
ax[0].set_ylabel('loss')
ax[0].legend()
ax[1].plot(np.array(log_train).T[1], label='train')
ax[1].plot(np.array(log_valid).T[1], label='valid')
ax[1].set_xlabel('epoch')
ax[1].set_ylabel('accuracy')
ax[1].legend()
plt.show()

76. チェックポイント

問題 75 のコードを改変し，各エポックのパラメータ更新が完了するたびに，チェックポイント（学習途中のパラメータ（重み行列など）の値や最適化アルゴリズムの内部状態）をファイルに書き出せ．

model = SimpleNet(300, 4)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)

num_epochs = 10
log_train = []
log_valid = []
for epoch in range(num_epochs):
  model.train()
  for inputs, labels in train_dl:
    optimizer.zero_grad()
    outputs = model(inputs)
    loss = criterion(outputs, labels)
    loss.backward()
    optimizer.step()

  loss_train, acc_train = calc_loss_and_accuracy(model, criterion, train_dl)
  loss_valid, acc_valid = calc_loss_and_accuracy(model, criterion, valid_dl)
  log_train.append([loss_train, acc_train])
  log_valid.append([loss_valid, acc_valid])

  torch.save({
                'epoch': epoch,
                'model_state_dict': model.state_dict(),
                'optimizer_state_dict': optimizer.state_dict()
             },
             f'checkpoint_{epoch + 1}.pt'
             )

77. ミニバッチ化

問題 76 のコードを改変し， $B$ 事例ごとに損失・勾配を計算し，行列 $W$ の値を更新せよ（ミニバッチ化）． $B$ の値を $1,2,4,8,\dots$ と変化させながら，1 エポックの学習に要する時間を比較せよ．

import time

def train_model(train_ds, valid_ds, batch_size, model, criterion, optimizer, num_epochs):
  train_dl = torch.utils.data.DataLoader(train_ds, batch_size=batch_size, shuffle=True)
  valid_dl = torch.utils.data.DataLoader(valid_ds, batch_size=len(valid_ds), shuffle=False)

  log_train = []
  log_valid = []
  for epoch in range(num_epochs):
    s_time = time.time()
    model.train()
    for inputs, labels in train_dl:
      optimizer.zero_grad()
      outputs = model(inputs)
      loss = criterion(outputs, labels)
      loss.backward()
      optimizer.step()

    loss_train, acc_train = calc_loss_and_accuracy(model, criterion, train_dl)
    loss_valid, acc_valid = calc_loss_and_accuracy(model, criterion, valid_dl)
    log_train.append([loss_train, acc_train])
    log_valid.append([loss_valid, acc_valid])

    torch.save({
        'epoch': epoch,
        'model_state_dict': model.state_dict(),
        'optimizer_state_dict': optimizer.state_dict()
        },
        f'checkpoint_{epoch + 1}.pt'
    )

    e_time = time.time()

    print(f'epoch: {epoch + 1}, loss_train: {loss_train:.3f}, accuracy_train: {acc_train:.3f}, loss_valid: {loss_valid:.3f}, accuracy_valid: {acc_valid:.3f}, {(e_time - s_time):.3f}sec')

  return {'train': log_train, 'valid': log_valid}

train_ds = Dataset(X_train, y_train)
valid_ds = Dataset(X_valid, y_valid)

model = SimpleNet(300, 4)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)

for batch_size in [2 ** i for i in range(11)]:
  print(f'batch size: {batch_size}')
  log = train_model(train_ds, valid_ds, batch_size, model, criterion, optimizer, 1)

>> batch size: 1
>> epoch: 1, loss_train: 0.337, accuracy_train: 0.884, loss_valid: 0.385, accuracy_valid: 0.869, 3.993sec
>> batch size: 2
>> epoch: 1, loss_train: 0.303, accuracy_train: 0.896, loss_valid: 0.348, accuracy_valid: 0.879, 2.457sec
>> batch size: 4
>> epoch: 1, loss_train: 0.292, accuracy_train: 0.899, loss_valid: 0.341, accuracy_valid: 0.881, 1.220sec
>> batch size: 8
>> epoch: 1, loss_train: 0.288, accuracy_train: 0.901, loss_valid: 0.337, accuracy_valid: 0.887, 0.802sec
>> batch size: 16
>> epoch: 1, loss_train: 0.286, accuracy_train: 0.901, loss_valid: 0.336, accuracy_valid: 0.887, 0.592sec
>> batch size: 32
>> epoch: 1, loss_train: 0.285, accuracy_train: 0.902, loss_valid: 0.334, accuracy_valid: 0.886, 0.396sec
>> batch size: 64
>> epoch: 1, loss_train: 0.285, accuracy_train: 0.901, loss_valid: 0.334, accuracy_valid: 0.887, 0.307sec
>> batch size: 128
>> epoch: 1, loss_train: 0.285, accuracy_train: 0.901, loss_valid: 0.334, accuracy_valid: 0.887, 0.246sec
>> batch size: 256
>> epoch: 1, loss_train: 0.285, accuracy_train: 0.901, loss_valid: 0.334, accuracy_valid: 0.887, 0.219sec
>> batch size: 512
>> epoch: 1, loss_train: 0.284, accuracy_train: 0.901, loss_valid: 0.334, accuracy_valid: 0.887, 0.195sec
>> batch size: 1024
>> epoch: 1, loss_train: 0.287, accuracy_train: 0.901, loss_valid: 0.334, accuracy_valid: 0.887, 0.198sec

78. GPU 上での学習

問題 77 のコードを改変し，GPU 上で学習を実行せよ．

def calc_loss_and_accuracy(model, criterion, loader, device):
  model.eval()
  loss = 0.0
  total = 0
  correct = 0
  with torch.no_grad():
    for inputs, labels in loader:
      inputs = inputs.to(device)
      labels = labels.to(device)
      outputs = model(inputs)
      loss += criterion(outputs, labels).item()
      pred = torch.argmax(outputs, dim=-1)
      total += len(inputs)
      correct += (pred == labels).sum().item()

  return loss / len(loader), correct / total


def train_model(train_ds, valid_ds, batch_size, model, criterion, optimizer, num_epochs, device=None):
  model.to(device)

  train_dl = torch.utils.data.DataLoader(train_ds,
                                         batch_size=batch_size,
                                         shuffle=True)
  valid_dl = torch.utils.data.DataLoader(valid_ds,
                                         batch_size=len(valid_ds),
                                         shuffle=False)

  log_train = []
  log_valid = []
  for epoch in range(num_epochs):
    s_time = time.time()
    model.train()
    for inputs, labels in train_dl:
      optimizer.zero_grad()
      inputs = inputs.to(device)
      labels = labels.to(device)
      outputs = model.forward(inputs)
      loss = criterion(outputs, labels)
      loss.backward()
      optimizer.step()

    loss_train, acc_train = calc_loss_and_accuracy(model, criterion, train_dl, device)
    loss_valid, acc_valid = calc_loss_and_accuracy(model, criterion, valid_dl, device)
    log_train.append([loss_train, acc_train])
    log_valid.append([loss_valid, acc_valid])

    torch.save({
        'epoch': epoch,
        'model_state_dict': model.state_dict(),
        'optimizer_state_dict': optimizer.state_dict()
        },
        f'checkpoint_{epoch + 1}.pt'
    )

    e_time = time.time()

    print(f'epoch: {epoch + 1}, loss_train: {loss_train:.3f}, accuracy_train: {acc_train:.3f}, loss_valid: {loss_valid:.3f}, accuracy_valid: {acc_valid:.3f}, {(e_time - s_time):.3f}sec')

  return {'train': log_train, 'valid': log_valid}

train_ds = Dataset(X_train, y_train)
valid_ds = Dataset(X_valid, y_valid)

model = SimpleNet(300, 4)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)

device = torch.device('cuda')

for batch_size in [2 ** i for i in range(11)]:
  print(f'batch size: {batch_size}')
  log = train_model(train_ds, valid_ds, batch_size, model, criterion, optimizer, 1, device=device)

>> batch size: 1
>> epoch: 1, loss_train: 0.337, accuracy_train: 0.883, loss_valid: 0.392, accuracy_valid: 0.868, 13.139sec
>> batch size: 2
>> epoch: 1, loss_train: 0.300, accuracy_train: 0.898, loss_valid: 0.357, accuracy_valid: 0.882, 4.998sec
>> batch size: 4
>> epoch: 1, loss_train: 0.291, accuracy_train: 0.901, loss_valid: 0.349, accuracy_valid: 0.885, 2.623sec
>> batch size: 8
>> epoch: 1, loss_train: 0.287, accuracy_train: 0.901, loss_valid: 0.346, accuracy_valid: 0.882, 1.589sec
>> batch size: 16
>> epoch: 1, loss_train: 0.285, accuracy_train: 0.902, loss_valid: 0.344, accuracy_valid: 0.886, 0.902sec
>> batch size: 32
>> epoch: 1, loss_train: 0.285, accuracy_train: 0.903, loss_valid: 0.343, accuracy_valid: 0.887, 0.544sec
>> batch size: 64
>> epoch: 1, loss_train: 0.284, accuracy_train: 0.903, loss_valid: 0.343, accuracy_valid: 0.887, 0.377sec
>> batch size: 128
>> epoch: 1, loss_train: 0.284, accuracy_train: 0.903, loss_valid: 0.343, accuracy_valid: 0.887, 0.292sec
>> batch size: 256
>> epoch: 1, loss_train: 0.284, accuracy_train: 0.903, loss_valid: 0.342, accuracy_valid: 0.887, 0.291sec
>> batch size: 512
>> epoch: 1, loss_train: 0.284, accuracy_train: 0.903, loss_valid: 0.342, accuracy_valid: 0.887, 0.145sec
>> batch size: 1024
>> epoch: 1, loss_train: 0.282, accuracy_train: 0.903, loss_valid: 0.342, accuracy_valid: 0.887, 0.126sec

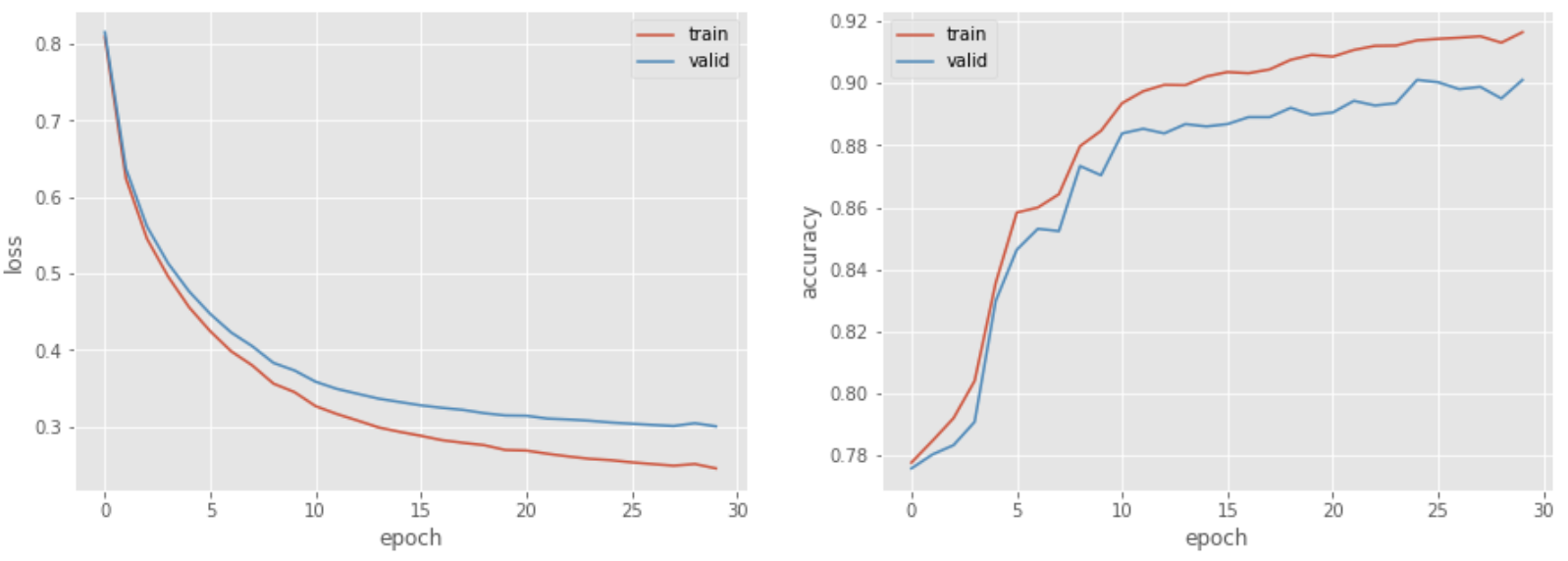
79. 多層ニューラルネットワーク

問題 78 のコードを改変し，バイアス項の導入や多層化など，ニューラルネットワークの形状を変更しながら，高性能なカテゴリ分類器を構築せよ．

from torch.nn import functional as F

class MLPNet(nn.Module):
  def __init__(self, input_size, mid_size, output_size):
    super().__init__()
    self.fc1 = nn.Linear(input_size, mid_size)
    self.act = nn.ReLU()
    self.fc2 = nn.Linear(mid_size, output_size)
    self.dropout = nn.Dropout(0.2)
    nn.init.kaiming_normal_(self.fc1.weight)
    nn.init.kaiming_normal_(self.fc2.weight)

  def forward(self, x):
    x = self.fc1(x)
    x = self.act(x)
    x = self.dropout(x)
    x = self.fc2(x)
    return x

model = MLPNet(300, 128, 4)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)

device = torch.device('cuda')

log = train_model(train_ds, valid_ds, 128, model, criterion, optimizer, 30, device=device)

fig, ax = plt.subplots(1, 2, figsize=(15, 5))
ax[0].plot(np.array(log['train']).T[0], label='train')
ax[0].plot(np.array(log['valid']).T[0], label='valid')
ax[0].set_xlabel('epoch')
ax[0].set_ylabel('loss')
ax[0].legend()
ax[1].plot(np.array(log['train']).T[1], label='train')
ax[1].plot(np.array(log['valid']).T[1], label='valid')
ax[1].set_xlabel('epoch')
ax[1].set_ylabel('accuracy')
ax[1].legend()
plt.show()

>> epoch: 1, loss_train: 0.809, accuracy_train: 0.778, loss_valid: 0.815, accuracy_valid: 0.776, 0.247sec
>> epoch: 2, loss_train: 0.624, accuracy_train: 0.785, loss_valid: 0.637, accuracy_valid: 0.780, 0.429sec
>> epoch: 3, loss_train: 0.545, accuracy_train: 0.792, loss_valid: 0.561, accuracy_valid: 0.783, 0.278sec
>> epoch: 4, loss_train: 0.496, accuracy_train: 0.804, loss_valid: 0.513, accuracy_valid: 0.791, 0.241sec
>> epoch: 5, loss_train: 0.456, accuracy_train: 0.836, loss_valid: 0.477, accuracy_valid: 0.830, 0.248sec
>> epoch: 6, loss_train: 0.425, accuracy_train: 0.858, loss_valid: 0.447, accuracy_valid: 0.846, 0.244sec
>> epoch: 7, loss_train: 0.398, accuracy_train: 0.860, loss_valid: 0.423, accuracy_valid: 0.853, 0.247sec
>> epoch: 8, loss_train: 0.380, accuracy_train: 0.864, loss_valid: 0.405, accuracy_valid: 0.852, 0.251sec
>> epoch: 9, loss_train: 0.356, accuracy_train: 0.880, loss_valid: 0.383, accuracy_valid: 0.873, 0.263sec
>> epoch: 10, loss_train: 0.345, accuracy_train: 0.885, loss_valid: 0.373, accuracy_valid: 0.870, 0.260sec
>> epoch: 11, loss_train: 0.327, accuracy_train: 0.894, loss_valid: 0.359, accuracy_valid: 0.884, 0.243sec
>> epoch: 12, loss_train: 0.317, accuracy_train: 0.897, loss_valid: 0.349, accuracy_valid: 0.885, 0.246sec
>> epoch: 13, loss_train: 0.308, accuracy_train: 0.899, loss_valid: 0.343, accuracy_valid: 0.884, 0.260sec
>> epoch: 14, loss_train: 0.299, accuracy_train: 0.899, loss_valid: 0.336, accuracy_valid: 0.887, 0.241sec
>> epoch: 15, loss_train: 0.293, accuracy_train: 0.902, loss_valid: 0.332, accuracy_valid: 0.886, 0.237sec
>> epoch: 16, loss_train: 0.288, accuracy_train: 0.904, loss_valid: 0.328, accuracy_valid: 0.887, 0.247sec
>> epoch: 17, loss_train: 0.282, accuracy_train: 0.903, loss_valid: 0.325, accuracy_valid: 0.889, 0.239sec
>> epoch: 18, loss_train: 0.279, accuracy_train: 0.904, loss_valid: 0.322, accuracy_valid: 0.889, 0.252sec
>> epoch: 19, loss_train: 0.276, accuracy_train: 0.908, loss_valid: 0.318, accuracy_valid: 0.892, 0.241sec
>> epoch: 20, loss_train: 0.269, accuracy_train: 0.909, loss_valid: 0.315, accuracy_valid: 0.890, 0.241sec
>> epoch: 21, loss_train: 0.269, accuracy_train: 0.909, loss_valid: 0.314, accuracy_valid: 0.891, 0.240sec
>> epoch: 22, loss_train: 0.265, accuracy_train: 0.911, loss_valid: 0.311, accuracy_valid: 0.894, 0.251sec
>> epoch: 23, loss_train: 0.261, accuracy_train: 0.912, loss_valid: 0.309, accuracy_valid: 0.893, 0.243sec
>> epoch: 24, loss_train: 0.258, accuracy_train: 0.912, loss_valid: 0.308, accuracy_valid: 0.894, 0.237sec
>> epoch: 25, loss_train: 0.256, accuracy_train: 0.914, loss_valid: 0.305, accuracy_valid: 0.901, 0.240sec
>> epoch: 26, loss_train: 0.253, accuracy_train: 0.914, loss_valid: 0.304, accuracy_valid: 0.900, 0.244sec
>> epoch: 27, loss_train: 0.251, accuracy_train: 0.915, loss_valid: 0.302, accuracy_valid: 0.898, 0.236sec
>> epoch: 28, loss_train: 0.249, accuracy_train: 0.915, loss_valid: 0.301, accuracy_valid: 0.899, 0.239sec
>> epoch: 29, loss_train: 0.251, accuracy_train: 0.913, loss_valid: 0.304, accuracy_valid: 0.895, 0.241sec
>> epoch: 30, loss_train: 0.245, accuracy_train: 0.916, loss_valid: 0.300, accuracy_valid: 0.901, 0.241sec