2022-05-15

ローレンツ曲線とジニ係数

ローレンツ曲線とは

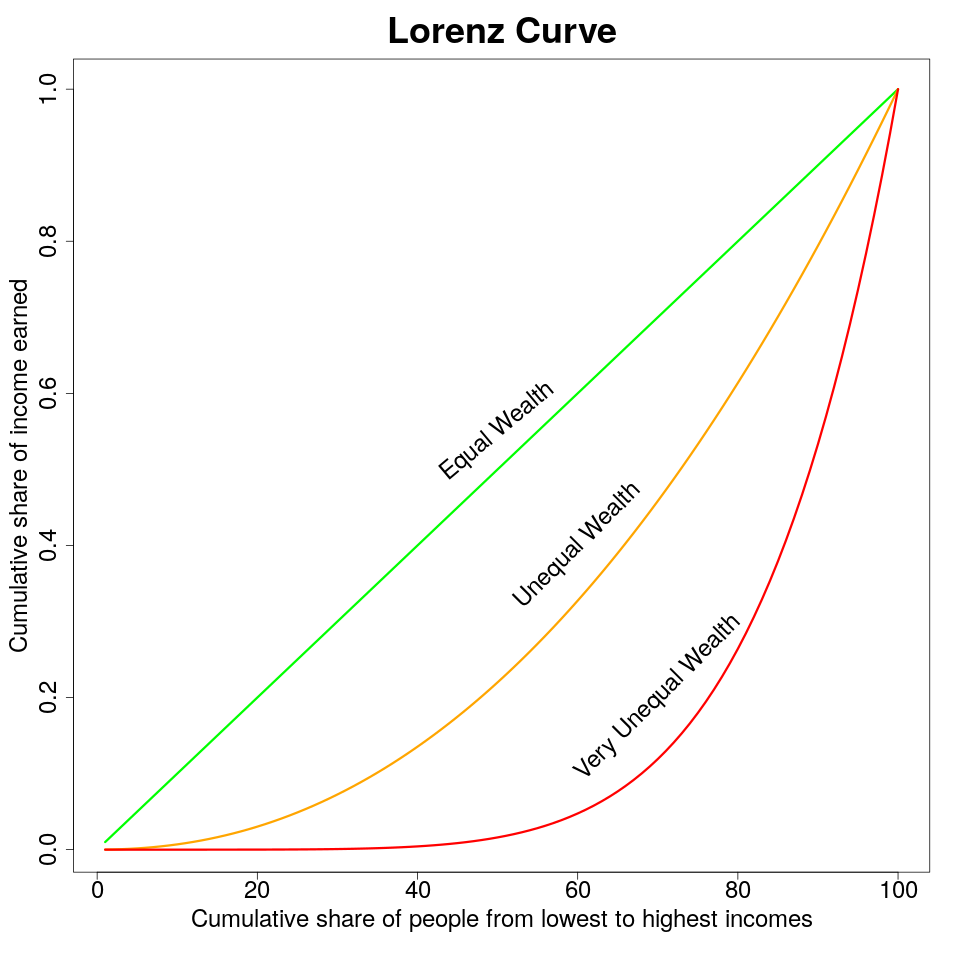
ローレンツ曲線は、人口内の富または所得の分布をグラフィカルに表したものです。この概念は、1905年にこの概念を発展させたアメリカの経済学者マックス・O・ローレンツにちなんで名付けられました。ローレンツ曲線は不平等の程度を明確に可視化し、異なる社会、経済、または時間の比較が可能です。

THE LORENZ CURVE

ローレンツ曲線の構築

ローレンツ曲線の構築は、人口を最貧層から最富層まで配列することから始まります。x軸は人口の累積割合を表し、y軸は総所得または総富の累積割合を示します。

グラフは、完全な平等の線として知られる45度の直線から始まります。全ての世帯が同じ所得を得ている場合、ローレンツ曲線はこの直線と一致します。言い換えれば、最下位10%の世帯は総所得の10%を持ち、最下位20%は所得の20%を持ち、これが100%に達するまで、順次続きます。

実際のローレンツ曲線は、平等の線よりも下に下がり、所得または富の分布の現実を示しています。この曲線の形状は、分布の不均衡性を表しています。例えば、最下位40%の世帯が総所得の10%しか持っていない場合、ローレンツ曲線はこの点で平等の線よりも大幅に下がります。

ローレンツ曲線の解釈

ローレンツ曲線は、経済的な不平等を解釈するための強力なツールです。曲線が完全な平等の線と一致する場合、所得または富の分布における完全な平等を示します。一方、ローレンツ曲線が軸と一致する場合（直角の曲線）、最大の不平等を表し、つまり一人が全ての所得または消費を持ち、他の全てが何も持っていない状況を意味します。

ジニ係数とは

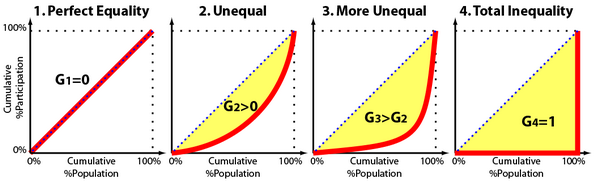
ジニ係数は、イタリアの統計学者コラード・ジニにちなんで名付けられた、国の住民の所得または富の分布を表す統計的なばらつきの尺度です。この係数は、0から1までの数値で表され、0は完全な平等を示し、全ての人が同じ所得を持ち、1は完全な不平等を示し、一人が全ての所得を持ち、他の全てが何も持っていない状態を表します。

Clearly Explained: Gini coefficient and Lorenz curve

ジニ係数の計算

ジニ係数は、ローレンツ曲線から導かれます。この係数は、完全な平等の線（45度の直線）とローレンツ曲線の間にある面積を、完全な平等の線の下の総面積に対する割合として表します。

数学的には、 $L(x)$ がローレンツ曲線である場合、ジニ係数 $G$ は次の式を用いて計算されます。

G = 1 - 2\int_0^1 (1-x)L(x)dx

この積分は、ローレンツ曲線の下の面積を表しています。完全な平等の線の下の全体の面積は0.5の三角形ですので、2倍の積分値は、ローレンツ曲線の下で完全な平等の線の下の面積の割合を示しています。これを1から引くことで、ジニ係数が得られます。

ジニ係数の応用

ジニ係数は、不平等を測るためにさまざまな分野で広く使用されています。経済学では、所得分配や富の不平等を測るために使用されます。健康分野では、医療提供の不均衡を理解するために使用されます。生態学者はジニ係数を生物多様性の指標として使用します。社会学者にとっては社会的なパラメータの不平等を測るための重要なツールです。

ジニ係数はまた、政策立案において重要な役割を果たします。政策立案者は、人口内の社会的経済的不平等に対処するためのリソースをどこに配分するかを決定する際に、この尺度を利用することができます。