ガンベル分布とは
ガンベル分布は、独立で同一分布の確率変数の最大値(または最小値)の挙動をモデル化する極値分布の一種です。自然災害、金融危機、エンジニアリング上の失敗などの極端な事象を解析するのに特に役立ちます。この分布は、位置パラメータ(
ガンベル分布:数学的基礎
確率密度関数(PDF)
連続型確率変数の値に対する確率密度関数です。ガンベル分布のPDFは次の式で与えられます。
ここで、
累積分布関数(CDF)
累積分布関数(CDF)は、確率変数が与えられた値次の値をとる確率を表します。ガンベル分布のCDFは、次の式で与えられます。
CDFは、分布の末尾の挙動に関する洞察を提供し、パーセンタイルやその他の要約統計量を計算するために使用できます。
モーメントと特性関数
モーメントは、分布の形状と中心傾向に関する重要な情報を提供します。ガンベル分布の
ここで、
特性関数は、分布を説明する別の方法であり、PDFのフーリエ変換として定義されます。ガンベル分布の特性関数は、次の式で与えられます。
ここで、
パラメータ推定:位置とスケール
ガンベル分布の位置パラメータ(
-
最尤推定法(MLE)
この方法は、分布のパラメータを与えられた観測データの尤度関数を最大化します。位置およびスケールパラメータの漸近的に偏りのない効率的な推定値を提供します。 -
モーメント法
このアプローチでは、サンプルモーメント(平均と分散)をガンベル分布の理論モーメントに一致させます。MLEに比べて効率は低いものの、一貫した推定値を提供します。
ガンベル分布の応用
この記事では、ガンベル分布の主要な応用(水文学、工学、金融、機械学習)について説明しています。
極値解析と水文学
水文学者は、洪水や干ばつのような極端な事象を解析するために、ガンベル分布を頼りにしています。これにより、事象の発生確率や規模を推定し、ダム、橋、堤防などのインフラ設計に貴重な洞察を提供します。極端な降雨量や河川の放流量の分布を理解することで、水文学者は水資源管理の改善や洪水緩和戦略の強化について熟考された決定を下すことができます。
エンジニアリングにおけるリスク評価
エンジニアリング分野では、ガンベル分布はリスク評価と管理において重要な役割を果たしています。エンジニアは、この分布を使用して、極限荷重や極端な環境条件下での構造物の破壊確率を分析します。構造物が耐えられる最大の応力や荷重を決定することで、より安全で信頼性の高いインフラを設計および維持することができます。この応用は、土木、構造、環境工学において特に関連があります。
ファイナンスにおけるポートフォリオ最適化
ガンベル分布は、投資ポートフォリオの最適化において、ファイナンス分野で貴重なツールです。ポートフォリオマネージャーは、しばしば金融資産の極端なリターンをモデル化するためにそれを使用し、極端な市場イベント中の潜在的な損失を推定することができます。ガンベル分布をValue-at-Risk(VaR)モデルやテールリスク分析に組み込むことで、投資家は潜在的な損失を最小限に抑え、リスク調整リターンを向上させるより熟考された決定を行うことができます。
機械学習と人工ニューラルネットワーク
近年、ガンベル分布は機械学習と人工ニューラルネットワークの分野にも進出しています。顕著な例の1つは、Gumbel-Softmax手法であり、強化学習や最適化問題において離散サンプリングに使用されます。Gumbel-Softmax手法は、ガンベル分布を利用して離散確率分布を近似することで、より効率的で安定したトレーニングプロセスを可能にします。さらに、研究者たちは、ガンベル分布をディープラーニングアルゴリズムにおいて、極端な事象(珍しいまたは異常なデータポイントなど)をモデル化する可能性を探っています。これにより、異常検出の改善やモデルのロバスト性の向上が期待されます。
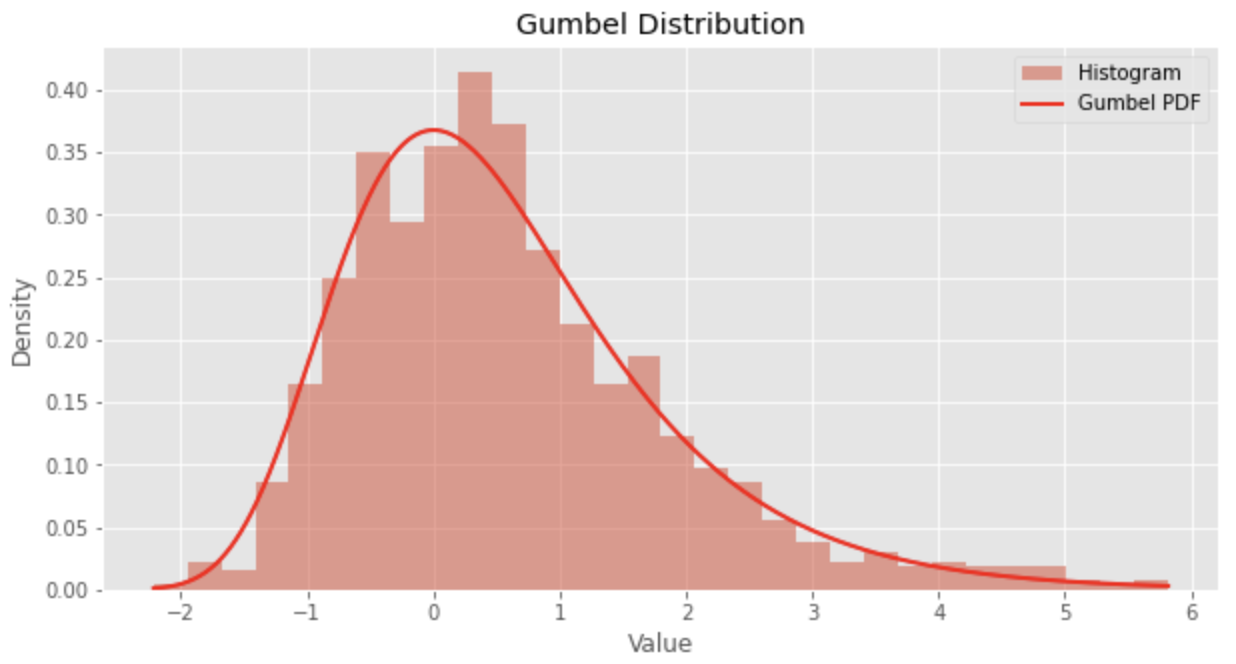
Pythonコード
以下は、Pythonでガンベル分布を描画するサンプルコードです。
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')
fig, ax = plt.subplots(facecolor="w", figsize=(10, 5))
# Gumbel distribution parameters
mu = 0 # Location parameter
sigma = 1 # Scale parameter
size = 1000 # Number of data points
# Generate Gumbel distributed data points
gumbel_data = np.random.gumbel(mu, sigma, size)
# Plot the histogram
plt.hist(gumbel_data, bins=30, density=True, alpha=0.5, label='Histogram')
# Calculate the Gumbel PDF
x = np.linspace(np.min(gumbel_data), np.max(gumbel_data), 1000)
pdf = (1/sigma) * np.exp(-(x-mu)/sigma - np.exp(-(x-mu)/sigma))
# Plot the Gumbel PDF
plt.plot(x, pdf, 'r-', lw=2, label='Gumbel PDF')
# Configure the plot
plt.title('Gumbel Distribution')
plt.xlabel('Value')
plt.ylabel('Density')
plt.legend()
# Show the plot
plt.show()