2022-11-11

EDAとは

EDA とは

EDAとは、Explanatory Data Analysisの略で、データを可視化したり、統計量を算出することによりデータの特徴や構造、パターンを理解する作業のことです。EDAは、データサイエンティストが機械学習モデルを構築するために一番最初に行う作業です。EDAをしっかり行い、データをきちんと理解し、仮説立てることが精度の高い機械学習モデルを構築するために必須になります。よく機械学習モデル開発に費やす時間のほとんどはEDAやデータの前処理、特徴量エンジニアリングと言われています。

EDAでは次のような分析を行います。

どれくらいのデータ量か
統計量（平均、分散など）はどうなっているか
分布はどうなっているか
欠損値はあるか
外れ値はあるか
データの相関はあるか
カテゴリ変数か数値変数か
- カテゴリ変数
  - カーディナリティ（ラベルのユニーク数）はどうなっているか
  - ラベルに優劣や順序があるか
  - 希少なラベルが含まれているか
- 数値変数：
  - 日付や年、時刻など時系列のデータがあるか
  - 値は離散的か連続的か

今回はKaggleのデータセットを使用して簡単なEDAを行なっていきます。

データセット

今回はKaggleの House Prices というコンペのデータセットを使用します。このコンペはアイオワ州Amesの各住宅の価格（SalePrice）を予測するというものです。

次のファイルをダウンロードします。

train.csv

必要なライブラリをインポートします。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import scipy.stats as stats

データセットをロードし、データを確認します。

df = pd.read_csv('train.csv')
pd.set_option('display.max_rows', None)

display(df.head())

カラムIdは不要なのでドロップします。

df.drop('Id', axis=1, inplace=True)
df.shape

(1460, 80)

このデータセットは1,460サンプル、 80カラムで構成されています。また、80カラムには目的変数SalePriceと79の説明変数があります。

目的変数の分布

まずは目的変数の分布を確認します。

df['SalePrice'].hist(bins=50, density=True)
plt.ylabel('Number of houses')
plt.xlabel('SalePrice')
plt.show()

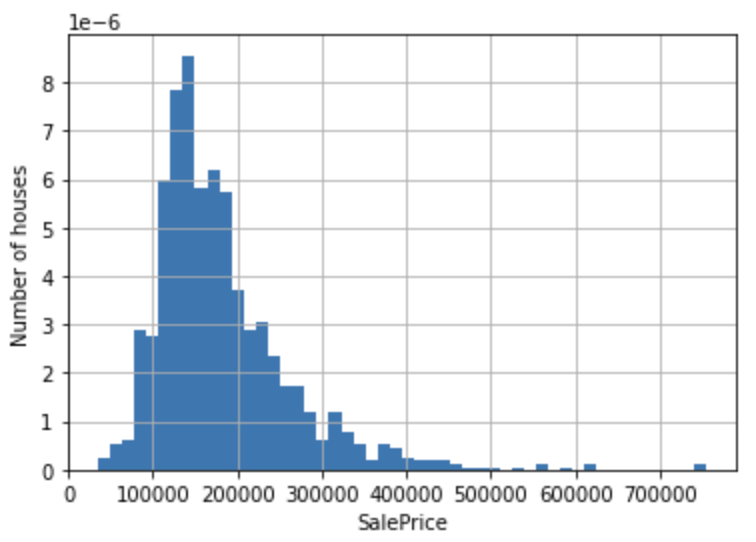
目的変数SalePriceの分布は右に歪んでいることが分かります。対数をとってこの歪みを改善します。

np.log(df['SalePrice']).hist(bins=50, density=True)
plt.ylabel('Number of houses')
plt.xlabel('Log of SalePrice')
plt.show()

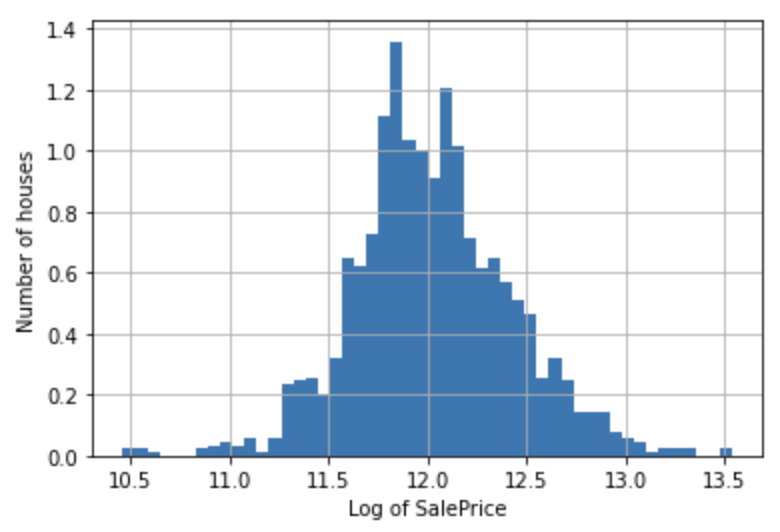
分布はより正規分布に近づきました。

説明変数のデータタイプ

カテゴリ変数と数値変数を特定します。

まずはカテゴリ変数を特定します。

cat_vars = [var for var in df.columns if df[var].dtype == 'O']

# MSSubClass is also categorical by definition, despite its numeric values
# so add MSSubClass to the list of categorical variables
cat_vars = cat_vars + ['MSSubClass']

print('number of categorical variables:', len(cat_vars))

number of categorical variables: 44

cat_varsに含まれるカラムをカテゴリカルデータにキャストしておきます。

df[cat_vars] = df[cat_vars].astype('O')

次に数値変数を特定します。

num_vars = [
    var for var in df.columns if var not in cat_vars and var != 'SalePrice'
]

print('number of categorical variables:', len(num_vars))

number of numerical variables: 35

欠損値

データセットのどの変数が欠損値を含むのかを確認します。

vars_with_na = [var for var in df.columns if data[var].isnull().sum() > 0]

df[vars_with_na].isnull().mean().sort_values(
    ascending=False).plot.bar(figsize=(10, 4))
plt.ylabel('% of missing data')
plt.axhline(y=0.80, color='r', linestyle='-')

plt.show()

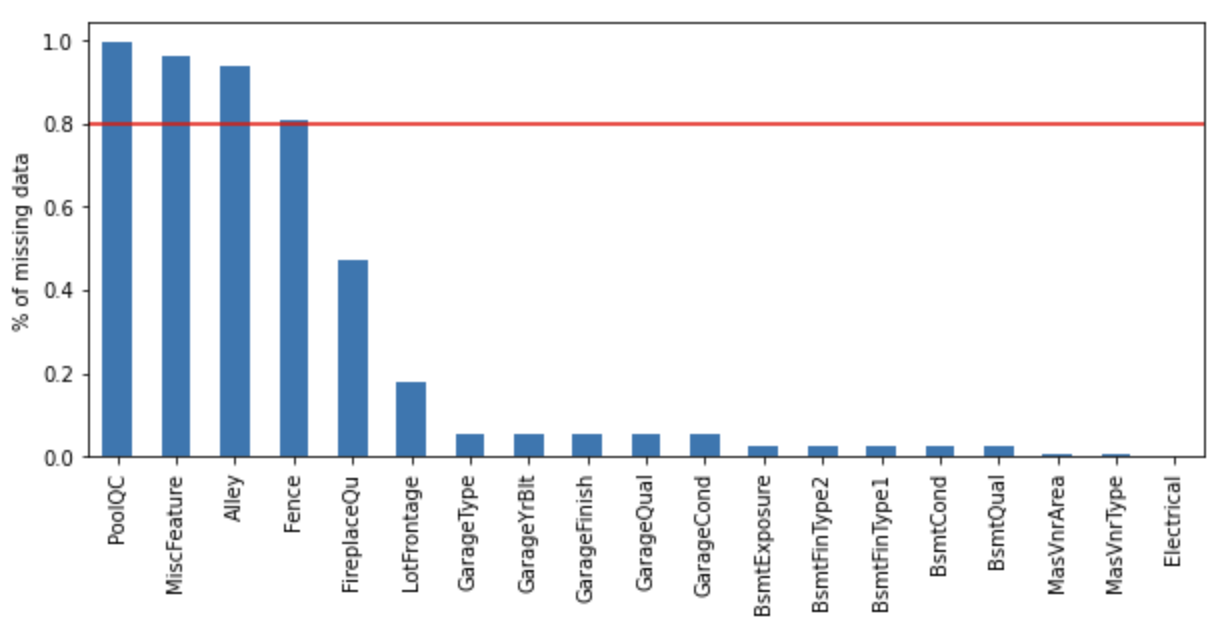
次のカラムは欠損率が80%を超えていることが分かります。

PoolQC
MiscFeature
Alley
Fence

数値変数

時系列値

データセットには年、月、日、時刻などといった時系列に関するデータが含まれている場合があります。今回は年に関するデータが含まれています。

year_vars = [var for var in num_vars if 'Yr' in var or 'Year' in var]
print(year_vars)

['YearBuilt', 'YearRemodAdd', 'GarageYrBlt', 'YrSold']

SalePriceとYrSoldの関係を可視化してみます。

df.groupby('YrSold')['SalePrice'].median().plot()
plt.ylabel('Median House Price')

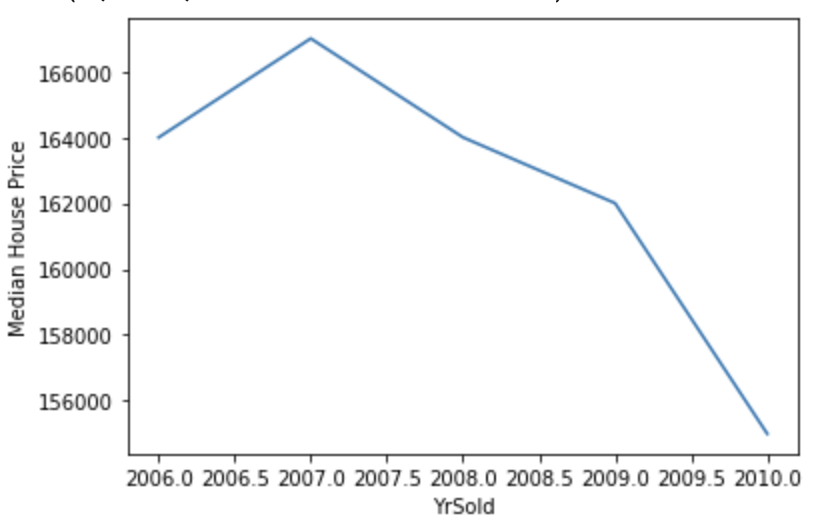
住宅の売却価格は年々減少傾向にあることが分かります。

離散値

取り得る値が有限である離散値を確認します。

discrete_vars = [var for var in num_vars if len(
    df[var].unique()) < 20 and var not in year_vars]


for var in discrete_vars:
    sns.catplot(x=var, y='SalePrice', data=df, kind="box", height=4, aspect=1.5)
    sns.stripplot(x=var, y='SalePrice', data=df, jitter=0.1, alpha=0.3, color='k')
    plt.show()

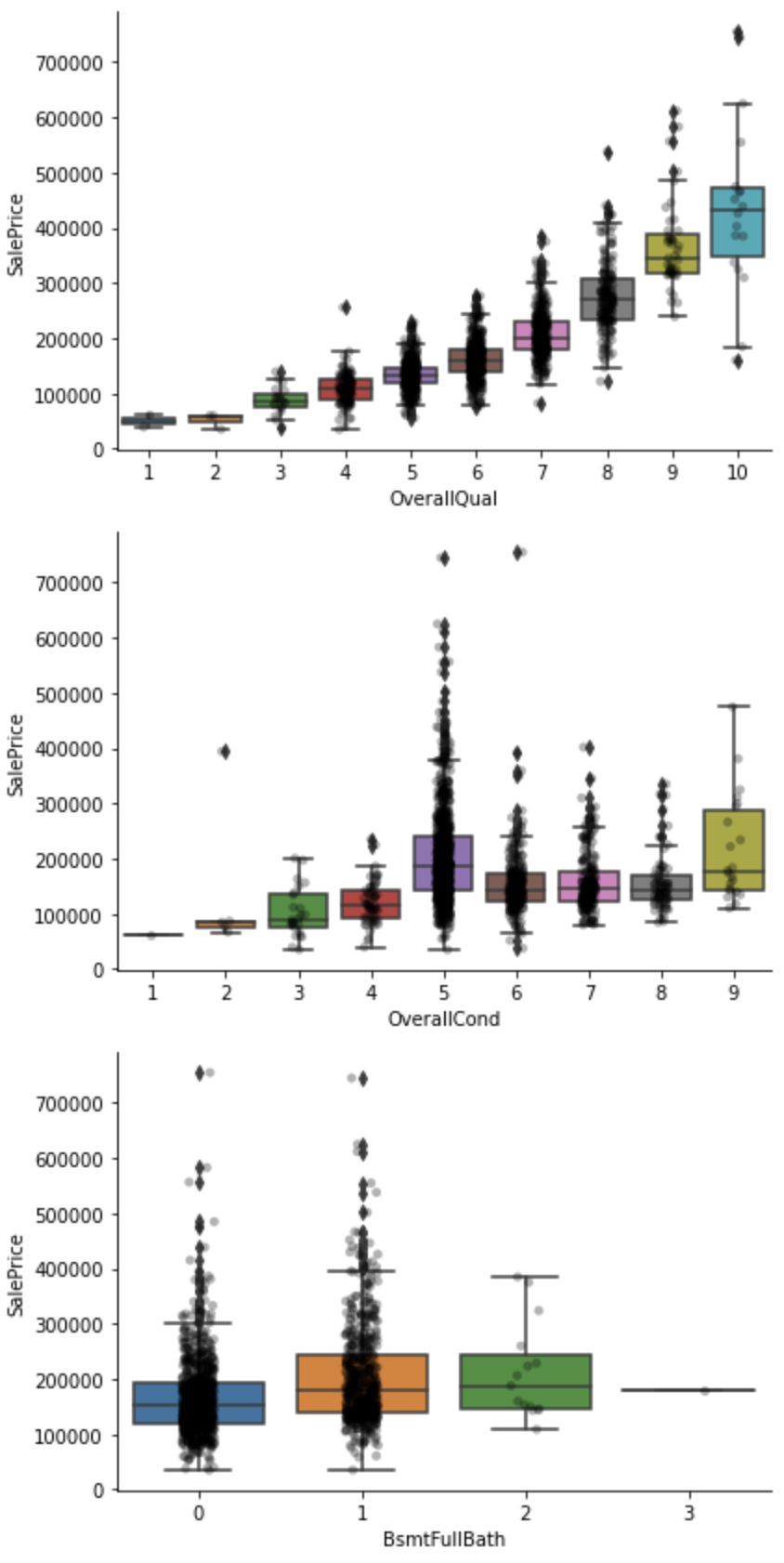
上のキャプチャのOverallQual、OverallCond、BsmtFullBathは値が大きくなるにつれて売却価格が上昇する傾向にあるようです。

連続値

連続値の分布を確認します。

cont_vars = [
    var for var in num_vars if var not in discrete_vars + year_vars]
df[cont_vars].hist(bins=30, figsize=(15,15))
plt.show()

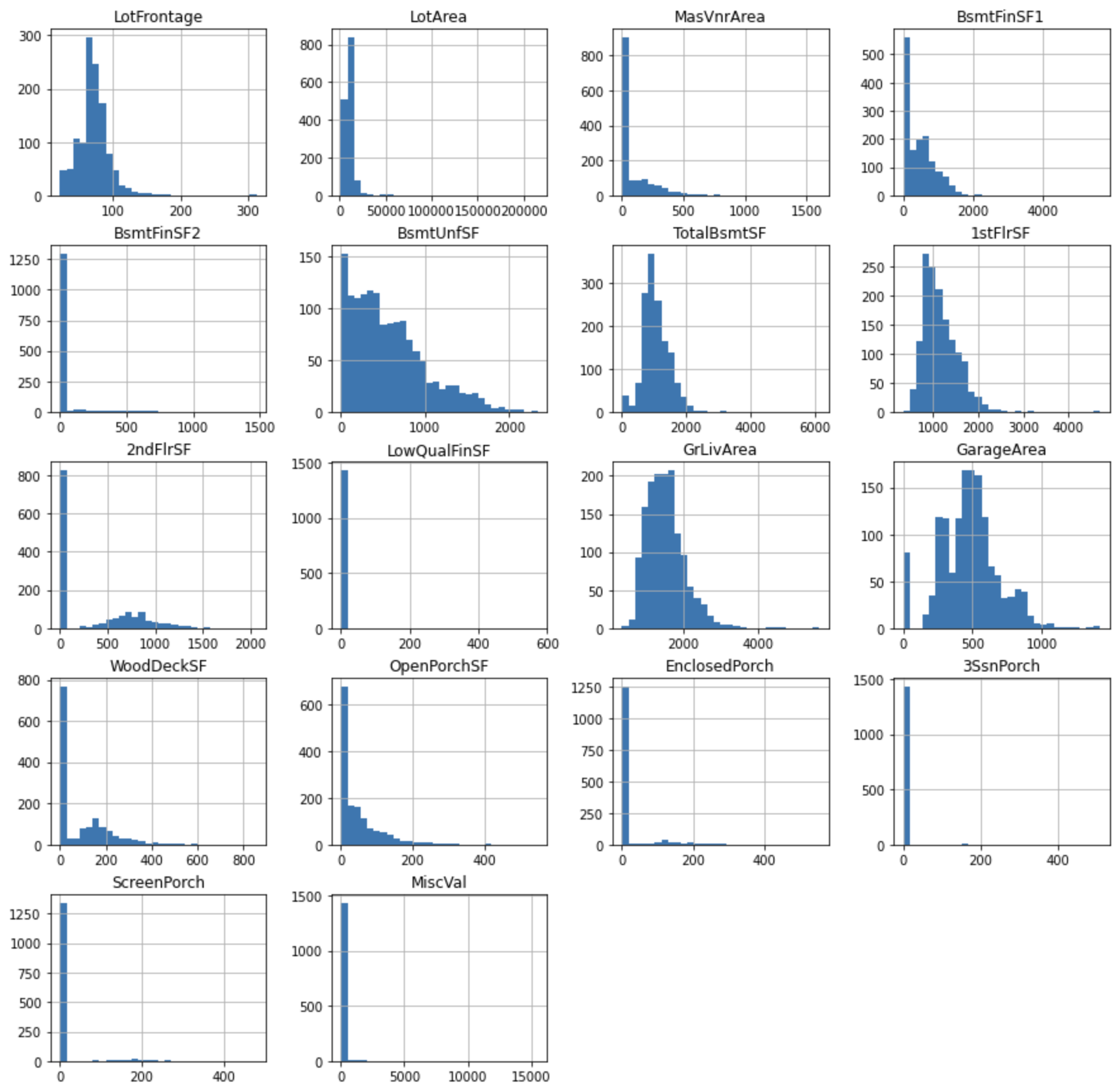
変数が正規分布でないことが確認できます。分布の歪みを改善するように変数を変換すると、モデルのパフォーマンスが向上する場合があります。

今回はLotFrontage, LotAreaなどの変数にYeo-Johnson変換を適用し、3SsnPorch, ScreenPorchなど極端な歪みがある変数に二値変換を適用します。

極端に歪んでいる変数をskewedに格納します。

skewed = [
    'BsmtFinSF2', 'LowQualFinSF', 'EnclosedPorch',
    '3SsnPorch', 'ScreenPorch', 'MiscVal'
]

cont_vars = [
    'LotFrontage',
    'LotArea',
    'MasVnrArea',
    'BsmtFinSF1',
    'BsmtUnfSF',
    'TotalBsmtSF',
    '1stFlrSF',
    '2ndFlrSF',
    'GrLivArea',
    'GarageArea',
    'WoodDeckSF',
    'OpenPorchSF',
]

Yeo-Johnson 変換

Yeo-Johnson変換を適用します。

tmp = df.copy()

for var in cont_vars:
    tmp[var], param = stats.yeojohnson(df[var])

tmp[cont_vars].hist(bins=30, figsize=(15,15))
plt.show()

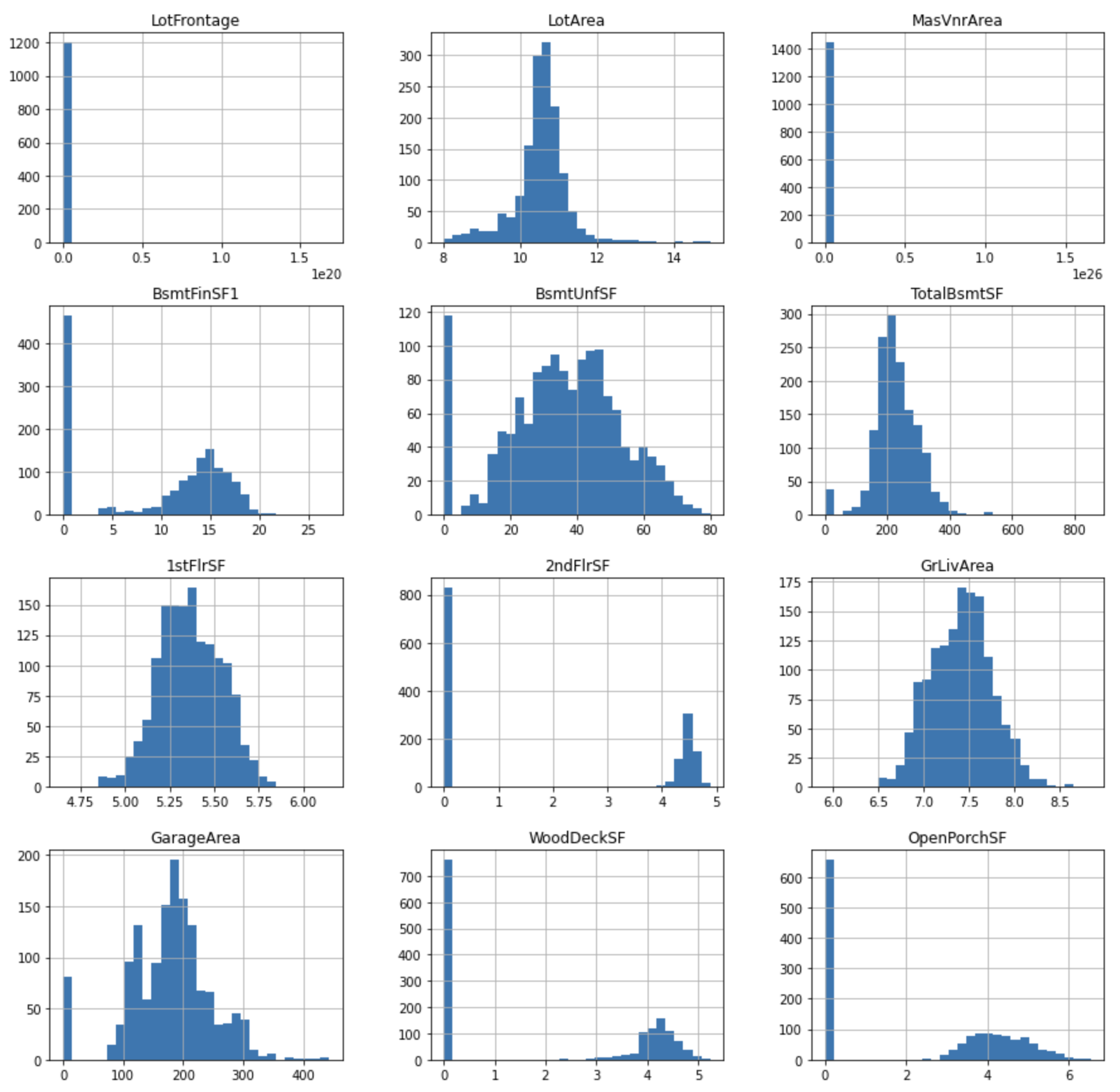
SalePriceとの関係を可視化してみます。

for var in cont_vars:
    plt.figure(figsize=(12,4))
    plt.subplot(1, 2, 1)
    plt.scatter(df[var], np.log(df['SalePrice']))
    plt.ylabel('SalePrice')
    plt.xlabel('Original ' + var)
    plt.subplot(1, 2, 2)
    plt.scatter(tmp[var], np.log(tmp['SalePrice']))
    plt.ylabel('SalePrice')
    plt.xlabel('Transformed ' + var)
    plt.show()

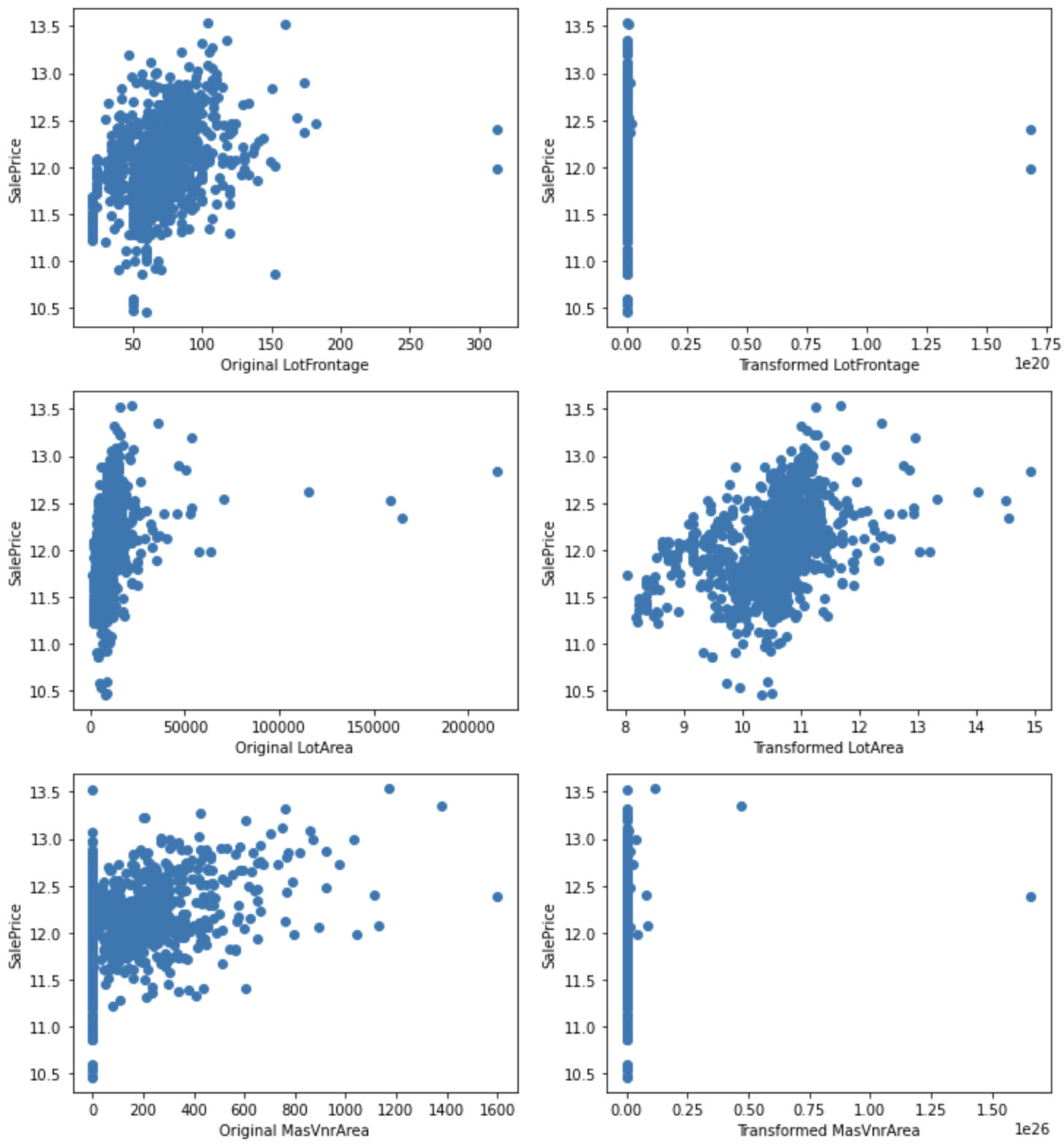
LotAreaについては、変換によりSalePriceとの関係が改善されました。

ほとんどの変数は0を含むため、対数変換を適用することができませんが、LotFrontage, 1stFlrSF GrLivAreaについては適用可能です。これらの変数について対数変換を行い、SalePriceとの関係が改善されるか確認します。

対数変換

tmp = df.copy()

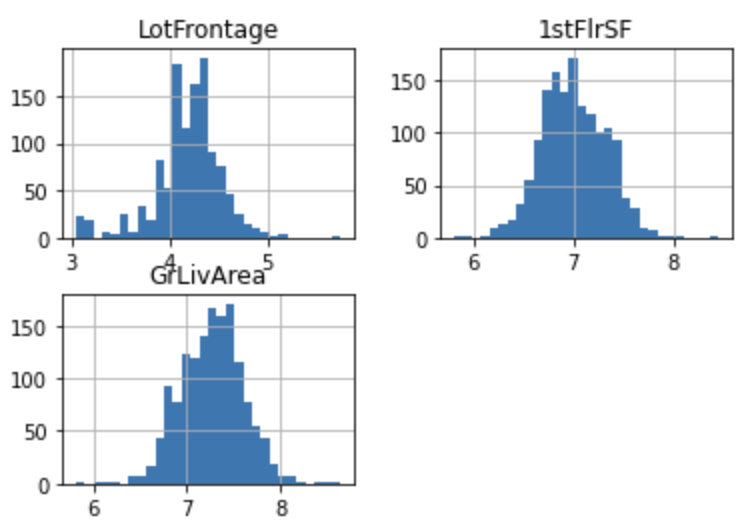
for var in ["LotFrontage", "1stFlrSF", "GrLivArea"]:
    tmp[var] = np.log(df[var])

tmp[["LotFrontage", "1stFlrSF", "GrLivArea"]].hist(bins=30)
plt.show()

for var in ["LotFrontage", "1stFlrSF", "GrLivArea"]:
    plt.figure(figsize=(12,4))
    plt.subplot(1, 2, 1)
    plt.scatter(df[var], np.log(df['SalePrice']))
    plt.ylabel('SalePrice')
    plt.xlabel('Original ' + var)

    plt.subplot(1, 2, 2)
    plt.scatter(tmp[var], np.log(tmp['SalePrice']))
    plt.ylabel('SalePrice')
    plt.xlabel('Transformed ' + var)

    plt.show()

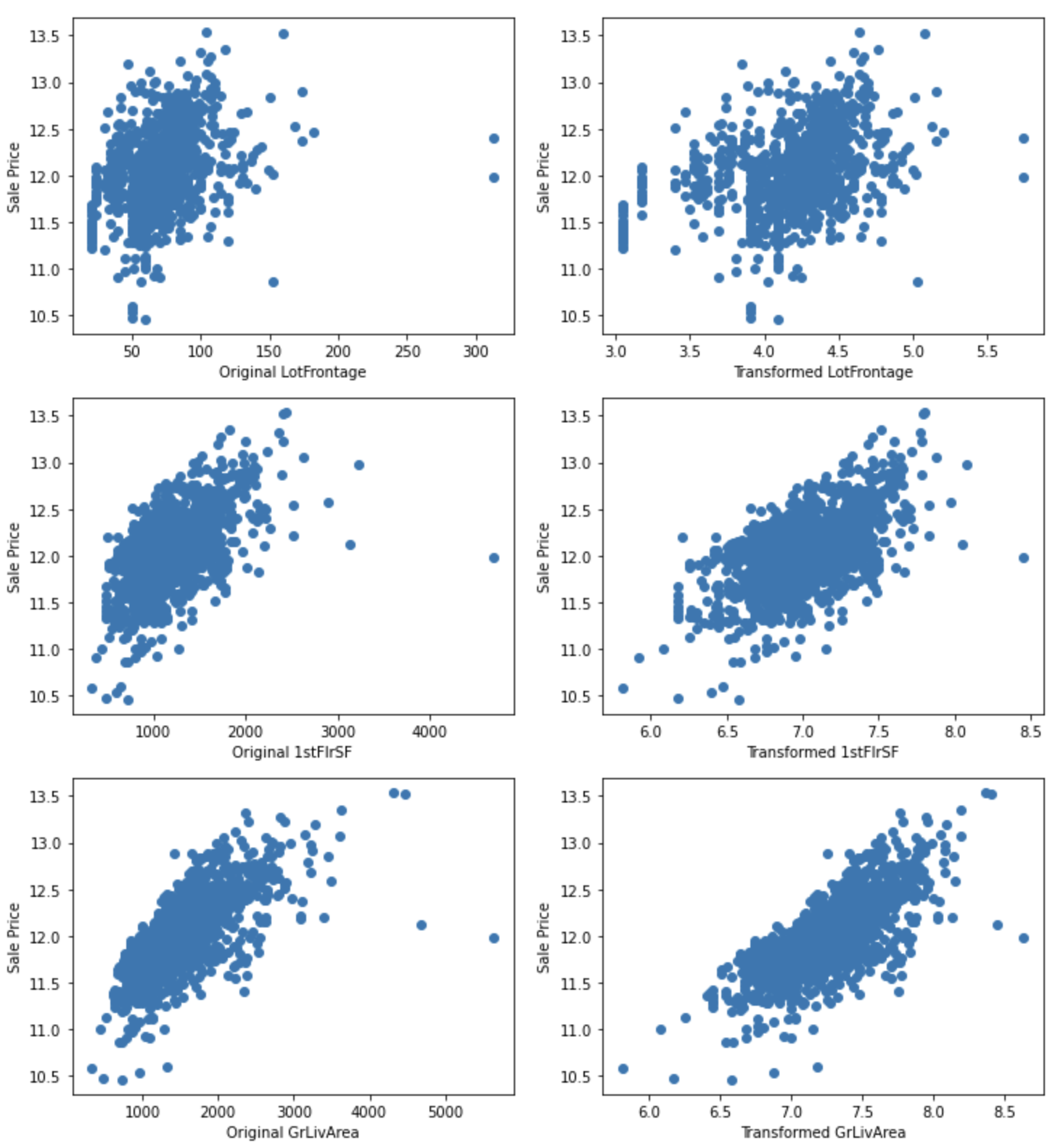
SalePriceとの関係が改善されているように見えます。

二値変換

極端に歪んでいる変数に対して二値変換を行います。

for var in skewed:
    tmp = df.copy()
    tmp[var] = np.where(df[var]==0, 0, 1)
    tmp = tmp.groupby(var)['SalePrice'].agg(['mean', 'std'])
    tmp.plot(kind="barh", y="mean", legend=False,
             xerr="std", title="Sale Price", color='green')
    plt.show()

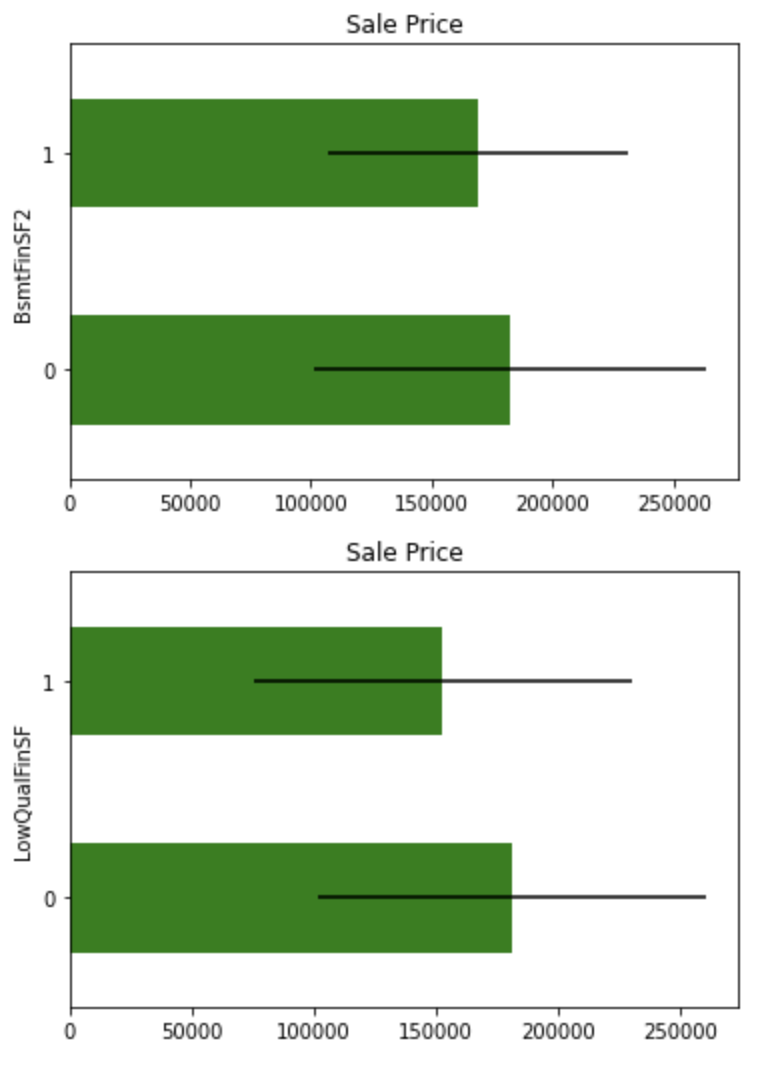
これらの変数は平均値に多少の違いがあるものの、信頼区間のオーバーラップがあるため、重要な説明変数でなさそうです。

カテゴリ変数

カーディナリティ

ユニークなカテゴリの数を確認します。

df[cat_vars].nunique().sort_values(ascending=False).plot.bar(figsize=(12,5))

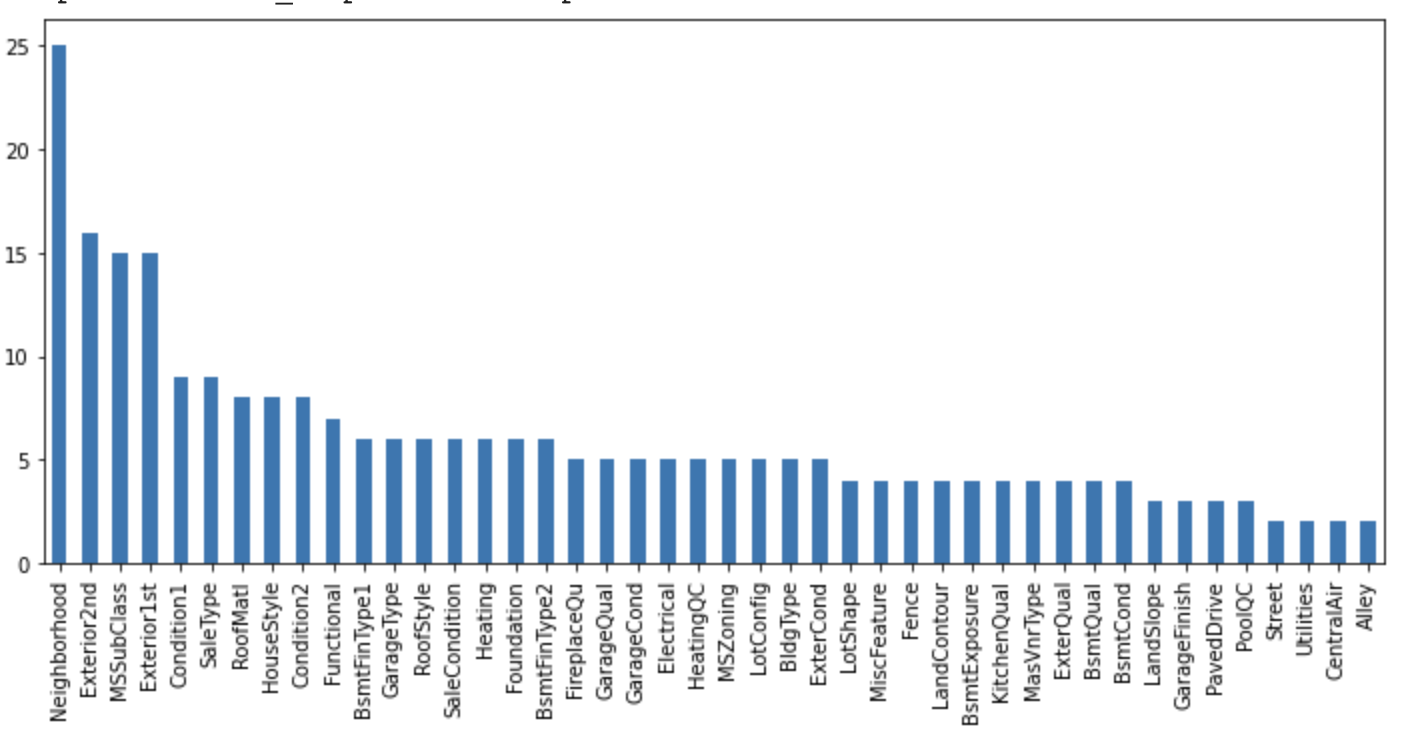
このデータセットのカテゴリ変数は、低いカーディナリティを示しています。

質ラベル

データセットのカテゴリ変数には、質を表す場合があり、その場合は数値に置き換えます。

今回のデータセットには次のように「Po」から「Ex」へと質が上がっていくカテゴリ変数が含まれています。これらを数値にマッピングします。

Ex: Excellent
Gd: Good
TA: Average/Typical
Fa: Fair
Po: Poor

qual_mappings = {'Po': 1, 'Fa': 2, 'TA': 3, 'Gd': 4, 'Ex': 5, 'Missing': 0, 'NA': 0}

qual_vars = ['ExterQual', 'ExterCond', 'BsmtQual', 'BsmtCond',
             'HeatingQC', 'KitchenQual', 'FireplaceQu',
             'GarageQual', 'GarageCond',
            ]

for var in qual_vars:
    df[var] = df[var].map(qual_mappings)

exposure_mappings = {'No': 1, 'Mn': 2, 'Av': 3, 'Gd': 4, 'Missing': 0, 'NA': 0}

var = 'BsmtExposure'

df[var] = df[var].map(exposure_mappings)

finish_mappings = {'Missing': 0, 'NA': 0, 'Unf': 1, 'LwQ': 2, 'Rec': 3, 'BLQ': 4, 'ALQ': 5, 'GLQ': 6}

finish_vars = ['BsmtFinType1', 'BsmtFinType2']

for var in finish_vars:
    df[var] = df[var].map(finish_mappings)

garage_mappings = {'Missing': 0, 'NA': 0, 'Unf': 1, 'RFn': 2, 'Fin': 3}

var = 'GarageFinish'

df[var] = df[var].map(garage_mappings)

fence_mappings = {'Missing': 0, 'NA': 0, 'MnWw': 1, 'GdWo': 2, 'MnPrv': 3, 'GdPrv': 4}

var = 'Fence'

df[var] = df[var].map(fence_mappings)

qual_vars  = qual_vars + finish_vars + ['BsmtExposure','GarageFinish','Fence']

for var in qual_vars:
    sns.catplot(x=var, y='SalePrice', data=df, kind="box", height=4, aspect=1.5)
    sns.stripplot(x=var, y='SalePrice', data=df, jitter=0.1, alpha=0.3, color='k')
    plt.show()

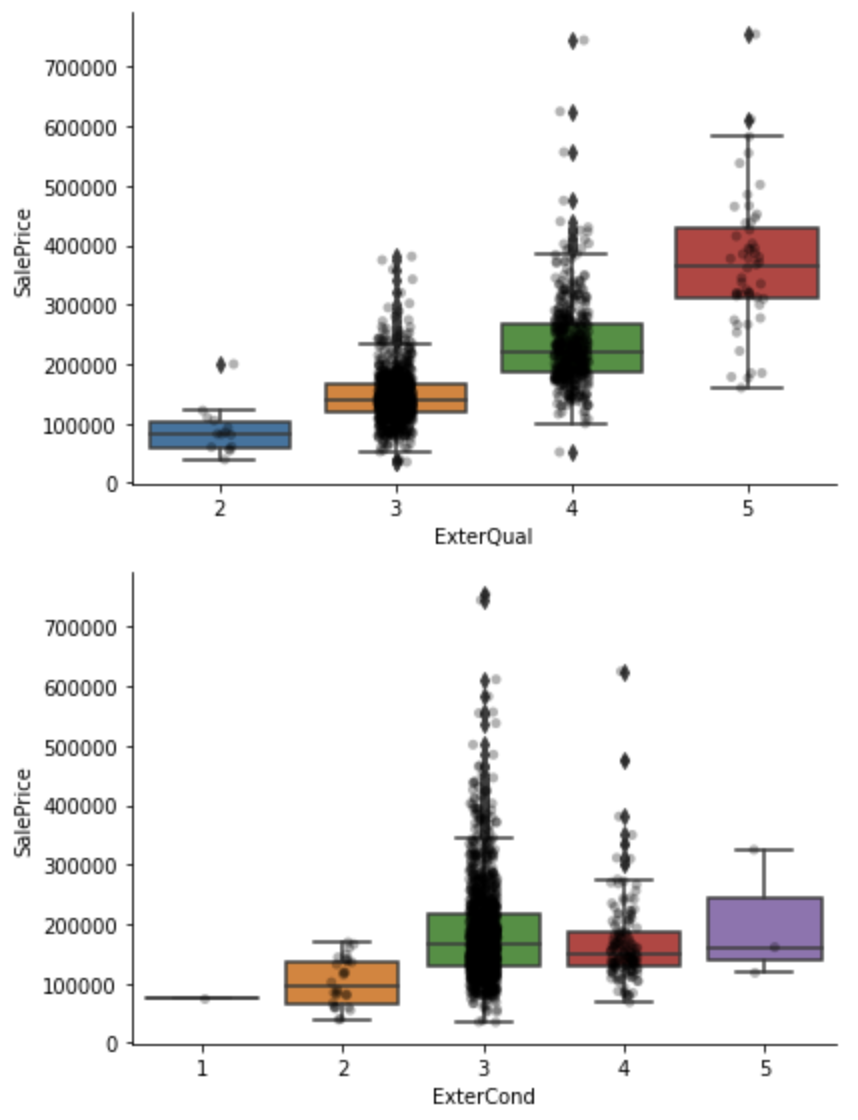
希少ラベル

カテゴリ変数の中には、1%未満しか存在しないラベルが存在する場合があります。データセットに過小に存在するラベルは、機械学習モデルのオーバーフィッティングを引き起こす傾向があるため、それらを除去しておく必要があります。次のコードでは出現率が1%次のラベルを抽出しています。

cat_others = [
    var for var in cat_vars if var not in qual_vars
]

def analyse_rare_labels(df_, var, rare_perc):
    df = df_.copy()
    tmp = df.groupby(var)['SalePrice'].count() / len(df)
    return tmp[tmp < rare_perc]

for var in cat_others:
    print(analyse_rare_labels(df, var, 0.01))
    print()

MSZoning
C (all)    0.006849
Name: SalePrice, dtype: float64

Street
Grvl    0.00411
Name: SalePrice, dtype: float64

.
.
.

おわりに

今回行ったEDAはほんの一例で、他に分析すべきことはたくさんあります。EDAをしっかり行い、データを深く理解することがデータサイエンティストには求められます。

参考

回帰問題の評価指標

回帰分析とは

Descriptive Statistics

Differential Equation

Dimensionality Reduction

Discrete Choice Model

Google Search Console

Hugging Face

Hypothesis Testing

Inferential Statistics

Probability Distribution

Ryusei Kakujo

Focusing on data science for mobility

Bench Press 100kg!