カイ二乗分布とは

カイ二乗分布とは、確率変数 X_1, X_2, \cdots, X_n が互いに独立であり、それぞれが標準正規分布 N(0,1) に従うとき、次の確率変数 \chi^2 が従う確率分布です。

カイ二乗分布の確率密度関数は次の式で表されます。

カイ二乗分布の確率密度関数は t 分布の確率密度関数と同様、パラメータが n のみとなっています。n はt分布と同様に自由度と呼ばれます。カイ二乗分布は \chi^2(n) と表されることもあります。

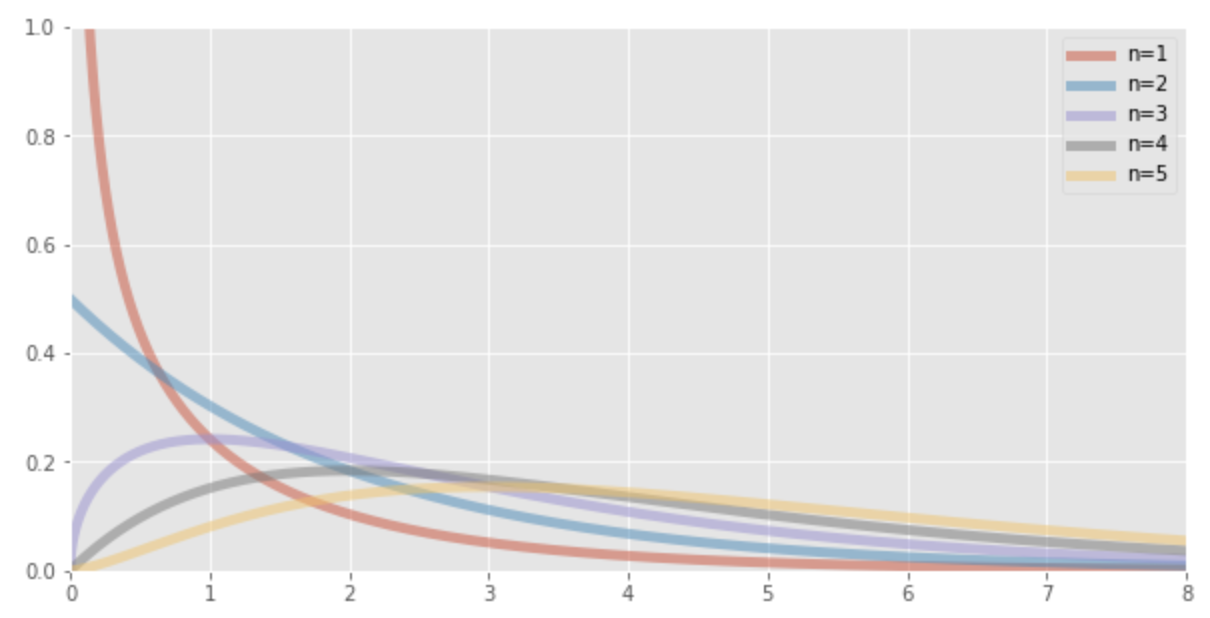
カイ二乗分布のグラフは自由度 n に依存し、次のようになります。

標準正規分布との関係

自由度が1のカイ二乗分布は、標準正規分布に従う確率変数 X_1 を二乗したものに等しくなります。

カイ二乗分布の期待値と分散

F分布 F(m, n) に従う確率変数 X の期待値、分散はそれぞれ以下になります。

カイ二乗分布表（上側）

カイ二乗分布はパラメータが n のみであるため、カイ二乗分布の確率をカイ二乗分布表と呼ばれる表にまとめることができます。以下に上側確率 \alpha がそれぞれ，0.1，0.05，0.025，0.01に一致するカイ二乗分布の自由度をまとめたカイ二乗分布表を示します。

例えば、自由度5のカイ二乗分布の上側5％点を求めたい場合は、n=10 と \alpha=0.05 の交差点の値を探します。したがって、求める上側5％点は11.07になります。

カイ二乗分布の再生性

確率変数 X と Y が次のようにそれぞれカイ二乗分布に従い、互いに独立であるとします。

このとき、X + Y は次のカイ二乗分布に従います。

この性質を再生性と言います。

正規分布に従う母集団からの無作為標本とカイ二乗分布

N(\mu,\sigma^2) の正規分布に従う母集団より無作為抽出された標本 X_1, X_2, \cdots, X_n において、それぞれの X は互いに独立に正規分布に従う場合、次の確率変数 W は自由度 n-1 のカイ二乗分布に従います。

また、不偏分散を S^2 とすると W は次のようにも表すことができます。

Python コード

以下にカイ二乗分布の描画で使用したPythonコードを示します。

from scipy.stats import chi2
import numpy as np
import matplotlib.pyplot as plt

plt.style.use('ggplot')
fig, ax = plt.subplots(facecolor="w", figsize=(10, 5))

x = np.linspace(0, 8, 10000)

k_deg = [1, 2, 3, 4, 5] # degree of freedom

for i in k_deg:
    plt.plot(x, chi2.pdf(x, i), linestyle='-', label='n={}'.format(i), lw=5, alpha=0.5)

plt.xlim(0, 8)
plt.ylim(0, 1)
plt.legend()
plt.show()