Apa itu Regresi Ridge

Regresi Ridge, juga dikenal sebagai regularisasi L2, adalah teknik regularisasi yang digunakan untuk mengatasi masalah multikolinieritas dalam model regresi linear. Multikolinieritas terjadi ketika variabel prediktor sangat berkorelasi, menghasilkan perkiraan koefisien regresi yang tidak stabil dan tidak dapat diandalkan. Dengan menambahkan term penalty dalam fungsi tujuan, regresi Ridge mempersempit koefisien regresi, menghasilkan model yang lebih stabil dan kuat.

Dasar Matematika

Fungsi Biaya

Dalam regresi linear, tujuannya adalah untuk menemukan hubungan antara fitur input (variabel independen) dan variabel target (variabel dependen) dengan memasangkan fungsi linear pada data. Fungsi biaya, juga dikenal sebagai fungsi tujuan atau fungsi kerugian, digunakan untuk mengukur kesalahan antara nilai yang diprediksi dan nilai aktual. Fungsi biaya yang paling umum digunakan dalam regresi linear adalah fungsi Mean Squared Error (MSE):

di mana:

• m adalah jumlah contoh pelatihan
• h_\theta(x^{(i)}) adalah nilai yang diprediksi untuk contoh ke-i
• y^{(i)} adalah nilai aktual untuk contoh ke-i
• \theta adalah vektor parameter model

Tujuan kita adalah untuk meminimalkan fungsi biaya J(\theta), yang berarti menemukan nilai optimal untuk parameter \theta yang menghasilkan kesalahan terendah.

Term Penalty L2

Dalam Regresi Ridge, kita menambahkan term penalty L2 ke dalam fungsi biaya untuk menghukum nilai parameter yang besar. Istilah regularisasi ini membantu mencegah overfitting dengan membatasi kompleksitas model. term penalty L2 didefinisikan sebagai:

di mana:

• \lambda adalah parameter regularisasi (juga dikenal sebagai koefisien ridge), yang mengontrol kekuatan regularisasi
• n adalah jumlah fitur (tidak termasuk istilah bias)
• \theta_j adalah parameter ke-j dalam vektor parameter \theta

Dengan term penalty L2, fungsi biaya untuk Regresi Ridge menjadi:

Tujuannya sekarang adalah untuk meminimalkan fungsi biaya yang dimodifikasi ini J(\theta) dengan menemukan nilai optimal untuk parameter \theta. Saat \lambda meningkat, term penalty memiliki efek yang lebih kuat pada fungsi biaya, menghasilkan model dengan bias yang lebih tinggi tetapi varian yang lebih rendah. Sebaliknya, ketika \lambda menurun, term penalty memiliki efek yang lebih lemah, menghasilkan model dengan bias yang lebih rendah tetapi varian yang lebih tinggi.

Menerapkan Regresi Ridge di Python

Pada bab ini, saya akan menunjukkan implementasi regresi Ridge di Python menggunakan kumpulan data perumahan California. Kita akan memplot hasil regresi linear dan regresi Ridge dengan berbagai parameter regularisasi untuk memahami efek mereka pada model.

Pertama, mari impor pustaka yang diperlukan:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, Ridge
from sklearn.metrics import mean_squared_error

Kemudian, kita akan memuat kumpulan data perumahan California dan memprosesnya dengan membaginya menjadi set pelatihan dan pengujian serta menskalakan fitur-fiturnya:

# Load the dataset
data = fetch_california_housing()
X, y = data['data'], data['target']

# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Scale the features
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

Kita akan memasangkan model regresi linear dan regresi Ridge dengan berbagai parameter regularisasi untuk membandingkan kinerjanya:

# Initialize models
linear_regression = LinearRegression()
ridge_regressions = [Ridge(alpha=alpha) for alpha in np.logspace(-3, 3, 7)]

# Fit models
linear_regression.fit(X_train_scaled, y_train)
for ridge_regression in ridge_regressions:
    ridge_regression.fit(X_train_scaled, y_train)

Kemudian, kita akan mengevaluasi model menggunakan mean squared error (MSE) dan membuat plot untuk memvisualisasikan hasilnya:

# Evaluate models
mse_linear_regression = mean_squared_error(y_test, linear_regression.predict(X_test_scaled))
mse_ridge_regressions = [mean_squared_error(y_test, ridge_regression.predict(X_test_scaled)) for ridge_regression in ridge_regressions]

# Set up the plot
plt.figure(figsize=(10, 6))
sns.set(style="whitegrid")
plt.xscale("log")
plt.xlabel("Regularization Parameter (alpha)")
plt.ylabel("Mean Squared Error")
plt.title("Linear Regression vs Ridge Regression")

# Plot the results
plt.plot(np.logspace(-3, 3, 7), [mse_linear_regression] * 7, label="Linear Regression", linestyle="--", marker="o", color="blue")
plt.plot(np.logspace(-3, 3, 7), mse_ridge_regressions, label="Ridge Regression", linestyle="--", marker="o", color="red")
plt.legend()

# Show the plot
plt.show()

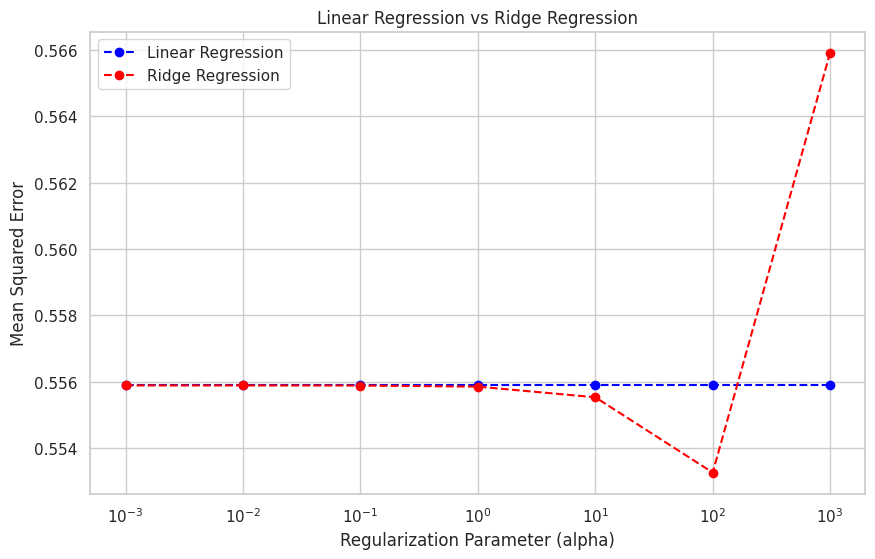
Plot menunjukkan mean squared error dari model regresi linear dan regresi Ridge untuk berbagai parameter regularisasi. Saat parameter regularisasi (alpha) meningkat, kinerja model regresi Ridge meningkat, awalnya melebihi kinerja model regresi linear. Namun, saat alpha terlalu besar, kinerja model regresi Ridge mulai menurun karena koefisien yang terlalu menyusut.