Apa itu Regresi Lasso

Regresi Lasso, juga dikenal sebagai Least Absolute Shrinkage and Selection Operator, adalah model regresi linear yang memperkenalkan regularisasi untuk meningkatkan kinerja dan interpretasi model. Tujuan utama dari Regresi Lasso adalah meminimalkan kompleksitas model dengan menambahkan L1 penalty pada fungsi biaya, yang membantu dalam seleksi fitur dan mencegah overfitting.

Perlunya Regularisasi

Dalam machine learning, overfitting terjadi saat model mempelajari noise pada data pelatihan dan berkinerja buruk pada data yang tidak dikenal. Regularisasi adalah teknik yang digunakan untuk mengatasi masalah ini dengan menambahkan penalty pada fungsi biaya. Dengan melakukan hal ini, model dipaksa untuk berfokus pada fitur yang paling relevan dan menghindari memasukkan noise.

Metode regularisasi dapat secara luas dikelompokkan menjadi dua kategori: regularisasi L1 dan regularisasi L2. Regresi Lasso menggunakan regularisasi L1, yang menghasilkan model yang jarang dengan mengatur beberapa koefisien menjadi nol. Sifat Regresi Lasso membuatnya menjadi kandidat ideal untuk seleksi fitur, terutama ketika menangani jumlah fitur yang besar.

Dasar Matematika Regresi Lasso

Fungsi Biaya

Dalam regresi linear, fungsi biaya, juga dikenal sebagai fungsi tujuan, digunakan untuk mengukur perbedaan antara nilai yang diprediksi dan nilai sebenarnya. Tujuannya adalah meminimalkan fungsi biaya ini untuk memperoleh koefisien optimal untuk model. Fungsi biaya untuk regresi linear diberikan oleh Mean Squared Error (MSE):

J(\boldsymbol{\beta}) = \frac{1}{n}\sum_{i=1}^n (y_i - \boldsymbol{x}_i^T \boldsymbol{\beta})^2

Di mana n adalah jumlah observasi, y_i mewakili output aktual, \boldsymbol{x}_i^T adalah transpose vektor input ke-i, dan \boldsymbol{\beta} adalah vektor koefisien.

Term Penalty L1

Dalam Regresi Lasso, term penalty L1 ditambahkan ke fungsi biaya untuk memperkenalkan regularisasi. Term penalty L1 diberikan oleh:

L1(\boldsymbol{\beta}) = \lambda \sum_{j=1}^p |\beta_j|

Di mana \lambda adalah parameter regularisasi, p adalah jumlah fitur, dan \beta_j adalah koefisien ke-j. Term penalty L1 mendorong kejarangan dengan memaksa beberapa koefisien menjadi tepat nol.

Lagrange Multiplier

Dengan menggabungkan term penalty L1 ke dalam fungsi biaya, kita memperoleh fungsi tujuan Regresi Lasso:

J(\boldsymbol{\beta}) = \frac{1}{n}\sum_{i=1}^n (y_i - \boldsymbol{x}i^T \boldsymbol{\beta})^2 + \lambda \sum{j=1}^p |\beta_j|

Lagrange multiplier, \lambda, mengontrol keseimbangan antara fitting data dan memaksakan kejarangan dalam model. Nilai \lambda yang lebih tinggi menghasilkan model yang lebih jarang, sedangkan nilai \lambda yang lebih rendah memungkinkan model untuk lebih cocok dengan data.

Solusi Jalur dan Batasan Lasso

Aspek kunci dari Regresi Lasso adalah jalur solusi, yang menggambarkan bagaimana perkiraan koefisien berubah sebagai fungsi dari parameter regularisasi, \lambda. Ketika \lambda meningkat, lebih banyak koefisien dipaksa menjadi nol, dan model menjadi lebih jarang.

Batasan Lasso dapat direpresentasikan secara geometris oleh bola norma L1 yang terpusat pada asal, dengan radius yang proposional dengan \frac{1}{\lambda}. Solusi Regresi Lasso sesuai dengan titik pertama di mana kontur fungsi biaya memotong bola norma L1. Karena geometri bola norma L1, solusi lebih cenderung berada pada sumbu, menghasilkan model yang jarang dengan beberapa koefisien yang tepat sama dengan nol.

Implementasi Regresi Lasso dalam Python

Dalam bab ini, saya akan mengimplementasikan Regresi Lasso menggunakan dataset California Housing dan memvisualisasikan transisi koefisien saat parameter regularisasi meningkat.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import fetch_california_housing
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

# Load the California Housing dataset
data = fetch_california_housing()
X = data['data']
y = data['target']
feature_names = data['feature_names']

# Split the dataset into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Standardize the data
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

# Set the range of regularization parameter values
lambdas = np.logspace(-4, 1, 100)

# Store the coefficients for each lambda value
coefficients = []

# Fit Lasso Regression for each lambda value and store the coefficients
for lmbda in lambdas:
    lasso = Lasso(alpha=lmbda, max_iter=10000)
    lasso.fit(X_train_scaled, y_train)
    coefficients.append(lasso.coef_)

# Plot the transition of coefficients using Matplotlib and Seaborn
plt.figure(figsize=(12, 8))
sns.set(style='whitegrid', palette='muted')

# Customize plot appearance
for i, feature in enumerate(feature_names):
    sns.lineplot(x=lambdas, y=np.array(coefficients)[:, i], label=feature)

plt.xscale('log')
plt.xlabel('Regularization Parameter (λ)', fontsize=14)
plt.ylabel('Coefficient Values', fontsize=14)
plt.title('Transition of Coefficients in Lasso Regression', fontsize=16, fontweight='bold')
plt.legend(fontsize=12, loc='upper right')

# Display the plot
plt.show()

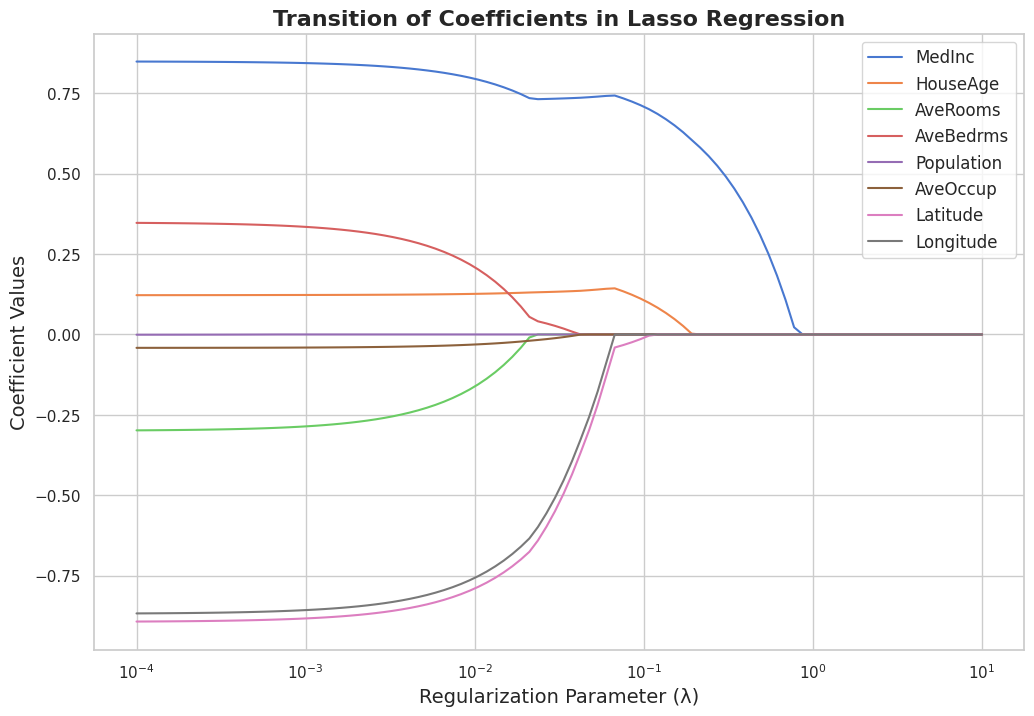
Skrip ini memuat dataset California Housing, membaginya menjadi set pelatihan dan pengujian, dan menstandarkan fiturnya. Kemudian, ia cocok dengan model Regresi Lasso untuk rentang nilai parameter regularisasi (\lambda) dan menyimpan koefisien.

Terakhir, ia menggunakan Matplotlib dan Seaborn untuk membuat plot yang menarik secara visual yang menampilkan transisi koefisien saat parameter regularisasi meningkat. Plot tersebut menunjukkan efek Regresi Lasso pada koefisien, menunjukkan bagaimana koefisien menyusut dan beberapa menjadi tepat nol saat \lambda meningkat. Ini adalah inti dari kemampuan Regresi Lasso untuk mempromosikan kejarangan dan melakukan seleksi fitur.