Apa itu Regularisasi
Regularisasi adalah teknik yang digunakan dalam pembelajaran mesin dan pemodelan statistik untuk mengurangi kompleksitas model dengan menambahkan istilah hukuman ke fungsi kerugian. Istilah hukuman ini mencegah overfitting dan memastikan model generalisasi dengan baik pada data yang belum pernah dilihat sebelumnya. Dengan kata lain, regularisasi membantu mencapai keseimbangan antara underfitting dan overfitting dengan membatasi kapasitas model untuk mempelajari pola-pola kompleks dalam data.
Pentingnya Regularisasi dalam Pembelajaran Mesin
Regularisasi memainkan peran penting dalam pembelajaran mesin karena beberapa alasan:
-
Mencegah Overfitting
Overfitting terjadi saat model mempelajari noise dalam data pelatihan, sehingga menghasilkan kinerja yang buruk pada data yang belum dilihat sebelumnya. Regularisasi membantu mencegah overfitting dengan memberikan hukuman pada model yang kompleks dan mendorong model yang lebih sederhana. -
Seleksi Fitur
Beberapa teknik regularisasi, seperti regularisasi L1, dapat mempromosikan sparsitas pada model dengan mereduksi beberapa koefisien menjadi nol. Hal ini efektif dalam melakukan seleksi fitur, membuat model lebih dapat diinterpretasi dan robust. -
Stabilitas
Teknik regularisasi, seperti regularisasi L2, dapat meningkatkan stabilitas model dengan mengurangi sensitivitas koefisien model terhadap perubahan kecil pada data masukan. -
Mengurangi Kompleksitas Model
Regularisasi membatasi kapasitas model, sehingga menghasilkan model yang lebih sederhana dan lebih mudah diinterpretasi serta dipelihara.
Overfitting dan Underfitting
Dalam pembelajaran mesin, tujuan akhir adalah membangun model yang generalisasi dengan baik pada data yang belum pernah dilihat sebelumnya. Namun, ada dua tantangan umum yang muncul selama proses pembuatan model: overfitting dan underfitting. Kedua hal ini dapat berdampak negatif pada kinerja model pada data baru.
-
Overfitting
Overfitting terjadi saat model mempelajari noise atau fluktuasi acak dalam data pelatihan alih-alih pola-pola mendasar. Akibatnya, model dapat bekerja sangat baik pada data pelatihan tetapi buruk pada data yang belum pernah dilihat sebelumnya. Overfitting umumnya terjadi ketika model terlalu kompleks dan memiliki variasi yang tinggi. -
Underfitting
Underfitting terjadi saat model terlalu sederhana untuk menangkap pola-pola mendasar dalam data. Akibatnya, model bekerja buruk pada data pelatihan dan data yang belum pernah dilihat sebelumnya. Underfitting adalah hasil dari bias yang tinggi pada model.
Regularisasi L1 (Lasso)
Regularisasi L1, juga dikenal sebagai Lasso (Least Absolute Shrinkage and Selection Operator), adalah teknik regularisasi yang menambahkan nilai absolut dari koefisien model ke dalam fungsi kerugian. Fungsi kerugian yang dimodifikasi untuk regularisasi L1 dapat direpresentasikan sebagai berikut:
di mana
Regularisasi L1 mendorong sparsitas pada model dengan mereduksi beberapa koefisien menjadi nol, sehingga efektif dalam melakukan seleksi fitur. Hal ini menghasilkan model yang lebih mudah diinterpretasi dan lebih sedikit kompleks.
Keuntungan
-
Seleksi Fitur
Regularisasi L1 dapat melakukan seleksi fitur, membuat model lebih mudah diinterpretasi dan lebih robust. -
Simplicity Model
Dengan mendorong sparsitas pada koefisien model, regularisasi L1 menghasilkan model yang lebih sederhana, lebih mudah diinterpretasi, dan lebih mudah dipelihara.
Kekurangan
-
Instabilitas
Regularisasi L1 dapat menyebabkan solusi yang tidak stabil ketika ada multikolinearitas antara fitur, karena cenderung memilih hanya satu fitur dari grup fitur yang berkorelasi. -
Tidak Sesuai untuk Dataset Kecil
Regularisasi L1 mungkin tidak berkinerja baik pada dataset kecil, karena sifatnya yang sparsitas dapat memperkenalkan bias tambahan.
Regularisasi L2 (Ridge)
Regularisasi L2, juga dikenal sebagai Ridge, adalah teknik regularisasi populer lainnya yang menambahkan kuadrat dari koefisien model ke dalam fungsi kerugian. Fungsi kerugian yang dimodifikasi untuk regularisasi L2 dapat direpresentasikan sebagai berikut:
di mana
Regularisasi L2 mendorong model untuk menggunakan semua fitur, namun dengan koefisien yang lebih kecil, mengurangi overfitting dan mempromosikan stabilitas.
Keuntungan
-
Stabilitas
Regularisasi L2 lebih stabil daripada regularisasi L1 dan bekerja dengan baik ketika ada multikolinearitas antara fitur, karena menyebar efek fitur yang berkorelasi di antara mereka. -
Bias yang Lebih Sedikit
Regularisasi L2 cenderung memperkenalkan bias yang lebih sedikit pada model dibandingkan regularisasi L1, sehingga lebih cocok untuk dataset yang lebih kecil.
Kekurangan
-
Tidak Ada Seleksi Fitur
Berbeda dengan regularisasi L1, regularisasi L2 tidak mendorong sparsitas pada koefisien model, dan oleh karena itu, tidak melakukan seleksi fitur. -
Model yang Kurang Dapat Diinterpretasi
Karena regularisasi L2 tidak mendorong sparsitas, model yang dihasilkan mungkin kurang dapat diinterpretasi dibandingkan dengan model yang dihasilkan menggunakan regularisasi L1.
Regularisasi Elastic Net
Regularisasi Elastic Net adalah teknik hibrida yang menggabungkan keuntungan dari regularisasi L1 dan L2. Ini menggabungkan nilai absolut dan kuadrat dari koefisien model dalam fungsi kerugian. Fungsi kerugian yang dimodifikasi untuk regularisasi Elastic Net dapat direpresentasikan sebagai berikut:
di mana
Regularisasi Elastic Net menyeimbangkan sifat induksi sparse dari regularisasi L1 dengan sifat promosi stabilitas dari regularisasi L2.
Keuntungan
-
Menyeimbangkan Regularisasi L1 dan L2
Regularisasi Elastic Net menyeimbangkan sifat induksi sparse dari regularisasi L1 dengan sifat promosi stabilitas dari regularisasi L2, sehingga menjadi pilihan yang cocok untuk berbagai masalah. -
Seleksi Fitur
Regularisasi Elastic Net dapat melakukan seleksi fitur sambil menjaga stabilitas model, tidak seperti regularisasi L1, yang dapat tidak stabil dalam kehadiran multikolinearitas.
Kekurangan
-
Kompleksitas Komputasi
Regularisasi Elastic Net memerlukan lebih banyak resource komputasi dibandingkan regularisasi L1 atau L2, karena melibatkan optimasi dua parameter regularisasi. -
Pemilihan Hyperparameter
Parameter tambahan, l1_ratio, perlu diatur, yang dapat meningkatkan kompleksitas proses pemilihan model.
Memilih Teknik Regularisasi yang Tepat
Memilih teknik regularisasi yang sesuai tergantung pada berbagai faktor, seperti ukuran dataset, keberadaan multikolinearitas, dan properti model yang diinginkan. Berikut beberapa panduan untuk membantu Anda memilih metode regularisasi yang tepat:
-
Ukuran Dataset
Untuk dataset kecil, regularisasi L2 umumnya lebih sesuai, karena memperkenalkan bias yang lebih sedikit dibandingkan regularisasi L1. Namun, untuk dataset yang lebih besar, regularisasi L1 dapat bermanfaat karena sifat induksi sparse yang menghasilkan model yang lebih mudah diinterpretasi. -
Multikolinearitas
Jika dataset Anda memiliki multikolinearitas antara fitur, regularisasi L2 atau Elastic Net mungkin lebih tepat, karena mereka menyebar efek fitur yang berkorelasi di antara mereka dan mempromosikan stabilitas. Regularisasi L1 mungkin tidak berfungsi dengan baik dalam hal ini, karena cenderung memilih hanya satu fitur dari grup fitur yang berkorelasi. -
Seleksi Fitur
Jika Anda menginginkan model yang melakukan seleksi fitur, regularisasi L1 atau Elastic Net mungkin merupakan pilihan yang cocok, karena mereka mendorong sparsitas pada koefisien model. Regularisasi L2 tidak melakukan seleksi fitur, karena tidak mendorong sparsitas. -
Interpretabilitas Model
Jika Anda memprioritaskan interpretabilitas model, regularisasi L1 dapat menjadi pilihan yang baik karena sifat induksi sparse-nya. Namun, regularisasi Elastic Net juga dapat menghasilkan model yang mudah diinterpretasi sambil menjaga stabilitas dalam kehadiran multikolinearitas.
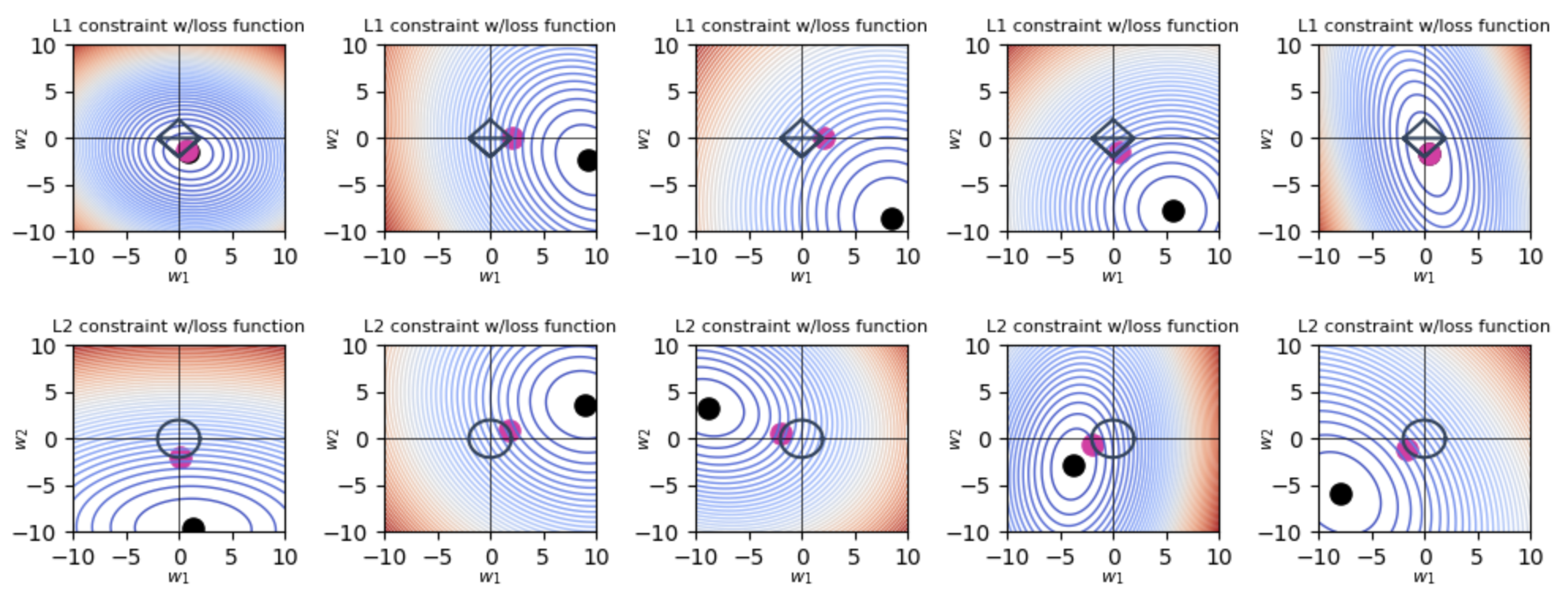
Visualisasi Regularisasi L1 dan L2
Berikut adalah skrip untuk memplotting regularisasi L1 dan L2 dengan Python.
Plotting 2D
import numpy as np
import matplotlib.pyplot as plt
import glob
import os
import warnings
lmbda = 2
w,h = 10,10
beta0 = np.linspace(-w, w, 100)
beta1 = np.linspace(-h, h, 100)
B0, B1 = np.meshgrid(beta0, beta1)
def diamond(lmbda=1, n=100):
"get points along diamond at distance lmbda from origin"
points = []
x = np.linspace(0, lmbda, num=n // 4)
points.extend(list(zip(x, -x + lmbda)))
x = np.linspace(0, lmbda, num=n // 4)
points.extend(list(zip(x, x - lmbda)))
x = np.linspace(-lmbda, 0, num=n // 4)
points.extend(list(zip(x, -x - lmbda)))
x = np.linspace(-lmbda, 0, num=n // 4)
points.extend(list(zip(x, x + lmbda)))
return np.array(points)
def circle(lmbda=1, n=100):
points = []
for angle in np.linspace(0,np.pi/2, num=n//4):
x = np.cos(angle) * lmbda
y = np.sin(angle) * lmbda
points.append((x,y))
for angle in np.linspace(np.pi/2,np.pi, num=n//4):
x = np.cos(angle) * lmbda
y = np.sin(angle) * lmbda
points.append((x,y))
for angle in np.linspace(np.pi, np.pi*3/2, num=n//4):
x = np.cos(angle) * lmbda
y = np.sin(angle) * lmbda
points.append((x,y))
for angle in np.linspace(np.pi*3/2, 2*np.pi,num=n//4):
x = np.cos(angle) * lmbda
y = np.sin(angle) * lmbda
points.append((x,y))
return np.array(points)
def loss(b0, b1,
a = 1,
b = 1,
c = 0,
cx = -10,
cy = 5):
return a * (b0 - cx) ** 2 + b * (b1 - cy) ** 2 + c * (b0 - cx) * (b1 - cy)
def select_parameters(lmbda, reg, force_symmetric_loss, force_one_nonpredictive):
while True:
a = np.random.random() * 10
b = np.random.random() * 10
c = np.random.random() * 4 - 1.5
if force_symmetric_loss:
b = a
c = 0
elif force_one_nonpredictive:
if np.random.random() > 0.5:
a = np.random.random() * 15 - 5
b = .1
else:
b = np.random.random() * 15 - 5
a = .1
c = 0
x, y = 0, 0
if reg=='L1':
while np.abs(x) + np.abs(y) <= lmbda:
x = np.random.random() * 2 * w - w
y = np.random.random() * 2 * h - h
else:
while np.sqrt(x**2 + y**2) <= lmbda:
x = np.random.random() * 2 * w - w
y = np.random.random() * 2 * h - h
Z = loss(B0, B1, a=a, b=b, c=c, cx=x, cy=y)
loss_at_min = loss(x, y, a=a, b=b, c=c, cx=x, cy=y)
if (Z >= loss_at_min).all():
break
return Z, a, b, c, x, y
def plot_loss(boundary, reg,
boundary_color='#2D435D',
boundary_dot_color='#E32CA6',
force_symmetric_loss=False, force_one_nonpredictive=False,
show_contours=True, contour_levels=50, show_loss_eqn=False,
show_min_loss=True,idx=None,fig=None,ax=None,num_trials=None):
Z, a, b, c, x, y = select_parameters(lmbda, reg,
force_symmetric_loss=force_symmetric_loss,
force_one_nonpredictive=force_one_nonpredictive)
eqn = f"{a:.2f}(b0 - {x:.2f})^2 + {b:.2f}(b1 - {y:.2f})^2 + {c:.2f} b0 b1"
n_col = 5
if show_loss_eqn:
ax[idx//n_col, idx%n_col].set_title(eqn, fontsize=10)
ax[idx//n_col, idx%n_col].set_xlabel("x", fontsize=8, labelpad=0)
ax[idx//n_col, idx%n_col].set_ylabel("y", fontsize=8, labelpad=-10)
ax[idx//n_col, idx%n_col].set_xticks([-10,-5,0,5,10])
ax[idx//n_col, idx%n_col].set_yticks([-10,-5,0,5,10])
ax[idx//n_col, idx%n_col].set_xlabel(r"$w_1$", fontsize=8)
ax[idx//n_col, idx%n_col].set_ylabel(r"$w_2$", fontsize=8)
shape = ""
if force_symmetric_loss:
shape = "symmetric "
elif force_one_nonpredictive:
shape = "orthogonal "
ax[idx//n_col, idx%n_col].set_title(f"{reg} constraint w/{shape}loss function", fontsize=8)
if show_contours:
ax[idx//n_col, idx%n_col].contour(B0, B1, Z, levels=contour_levels, linewidths=1.0, cmap='coolwarm')
else:
ax[idx//n_col, idx%n_col].contourf(B0, B1, Z, levels=contour_levels, cmap='coolwarm')
ax[idx//n_col, idx%n_col].plot([-w,+w],[0,0], '-', c='k', lw=.5)
ax[idx//n_col, idx%n_col].plot([0, 0],[-h,h], '-', c='k', lw=.5)
if boundary is not None:
ax[idx//n_col, idx%n_col].plot(boundary[:,0], boundary[:,1], '-', lw=1.5, c=boundary_color)
if show_min_loss:
ax[idx//n_col, idx%n_col].scatter([x],[y], s=90, c='k')
eqn = f"{a:.2f}(b0 - {x:.2f})^2 + {b:.2f}(b1 - {y:.2f})^2 + {c:.2f} (b0-{x:.2f}) (b1-{y:.2f})"
if boundary is not None:
losses = [loss(*edgeloc, a=a, b=b, c=c, cx=x, cy=y) for edgeloc in boundary]
minloss_idx = np.argmin(losses)
coeff = boundary[minloss_idx]
ax[idx//n_col, idx%n_col].scatter([coeff[0]], [coeff[1]], s=90, c=boundary_dot_color)
if force_symmetric_loss:
if reg=='L2':
ax[idx//n_col, idx%n_col].plot([x,0],[y,0], ':', c='k')
else:
ax[idx//n_col, idx%n_col].plot([x,coeff[0]],[y,coeff[1]], ':', c='k')
def plot_2d(reg, force_symmetric_loss=False, force_one_nonpredictive=False,num_trials=None):
if num_trials <=5:
fig,ax = plt.subplots(1,5,figsize=(10,2),squeeze=False)
elif num_trials > 5 and num_trials<=10:
fig,ax = plt.subplots(2,5,figsize=(10,4))
elif num_trials > 10 and num_trials<=15:
fig,ax = plt.subplots(3,5,figsize=(10,6))
fig.subplots_adjust(hspace=0.6, wspace=0.4)
if reg == 'L1':
boundary = diamond(lmbda=lmbda, n=100)
else:
boundary = circle(lmbda=lmbda, n=100)
for i in range(num_trials):
plot_loss(boundary=boundary, reg=reg,
force_symmetric_loss=force_symmetric_loss,
force_one_nonpredictive=force_one_nonpredictive,
contour_levels=contour_levels,idx=i,fig=fig,ax=ax,num_trials=num_trials)
shape_fname = ""
if force_symmetric_loss:
shape_fname = "symmetric-"
elif force_one_nonpredictive:
shape_fname = "orthogonal-"
plt.tight_layout()
if num_trials%5!=0:
k = 5*(1 + num_trials//5)-num_trials
for i in range(k):
fig.delaxes(ax[num_trials//5][-i-1])
plt.show()
n_trials = 5
contour_levels=50
s = 0
np.random.seed(s)
for mode in ["L1", "L2"]:
plot_2d(reg=mode,num_trials=n_trials)
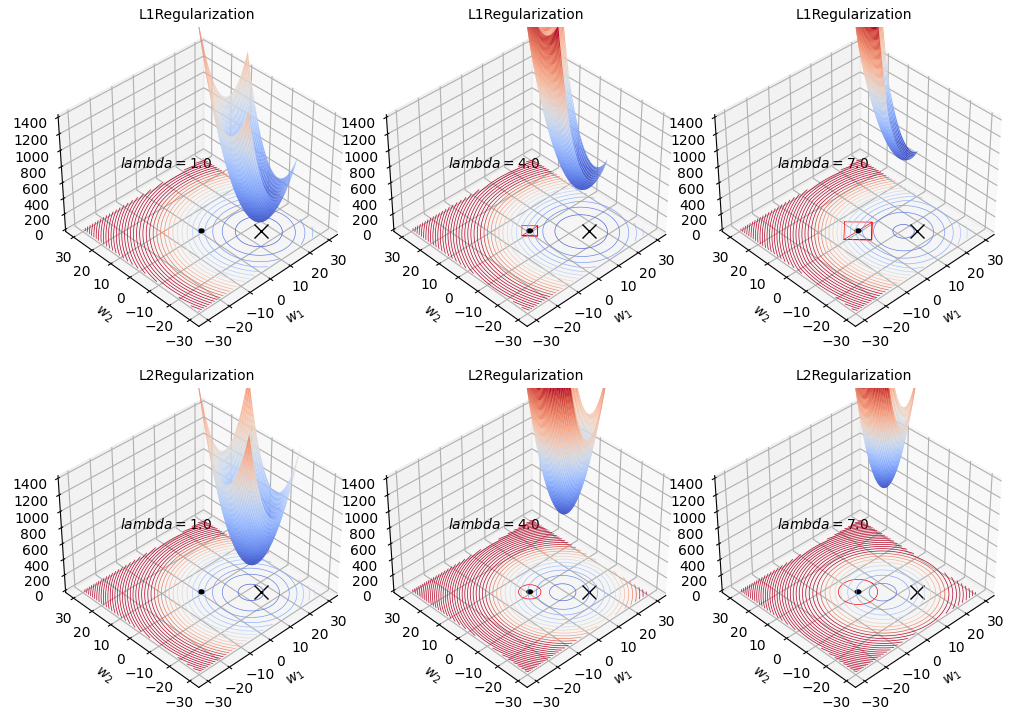
Plotting 3D
# https://github.com/parrt/website-explained.ai/blob/master/regularization/code/l2loss_with_penalty.py
import numpy as np
from matplotlib import pyplot as plt
from matplotlib import animation
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
from matplotlib.patches import Circle
import mpl_toolkits.mplot3d.art3d as art3d
import glob
import os
from PIL import Image as PIL_Image
def diamond(lmbda=1, n=100):
"get points along diamond at distance lmbda from origin"
points = []
x = np.linspace(0, lmbda, num=n // 4)
points.extend(list(zip(x, -x + lmbda)))
x = np.linspace(0, lmbda, num=n // 4)
points.extend(list(zip(x, x - lmbda)))
x = np.linspace(-lmbda, 0, num=n // 4)
points.extend(list(zip(x, -x - lmbda)))
x = np.linspace(-lmbda, 0, num=n // 4)
points.extend(list(zip(x, x + lmbda)))
return np.array(points)
def circle(lmbda=1, n=100):
points = []
for angle in np.linspace(0,np.pi/2, num=n//4):
x = np.cos(angle) * lmbda
y = np.sin(angle) * lmbda
points.append((x,y))
for angle in np.linspace(np.pi/2,np.pi, num=n//4):
x = np.cos(angle) * lmbda
y = np.sin(angle) * lmbda
points.append((x,y))
for angle in np.linspace(np.pi, np.pi*3/2, num=n//4):
x = np.cos(angle) * lmbda
y = np.sin(angle) * lmbda
points.append((x,y))
for angle in np.linspace(np.pi*3/2, 2*np.pi,num=n//4):
x = np.cos(angle) * lmbda
y = np.sin(angle) * lmbda
points.append((x,y))
return np.array(points)
def loss(b0, b1,
a = 1,
b = 1,
c = 0, # axis stretch
cx = -10, # shift center x location
cy = 5, # shift center y
lmbda=1.0,
yintercept=100):
eqn = f"{a:.2f}(b0 - {cx:.2f})^2 + {b:.2f}(b1 - {cy:.2f})^2 + {c:.2f} (b0-{cx:.2f}) (b1-{cy:.2f}) + {yintercept}"
return lmbda * (a * (b0 - cx) ** 2 + b * (b1 - cy) ** 2) + c * (b0 - cx) * (b1 - cy) + yintercept
def loss_l1(b0,b1,a=1,b=1,c=0,cx=-10,cy=5,lmbda=1.0,yintercept=100):
return lmbda*(a*np.abs(b0-cx) + b*np.abs(b1-cy))
def plot_3d(mode, last_lmbda, stepsize, lmbdas):
fig = plt.figure(figsize=(10,10))
plt.subplots_adjust(wspace=0.4, hspace=2.0)
for i,lmbda in enumerate(lmbdas):
ax = fig.add_subplot(3,3,i+1, projection='3d')
ax.set_xlabel("$w_1$", labelpad=0)
ax.set_ylabel("$w_2$", labelpad=0)
ax.set_title(mode + "Regularization",fontsize=10)
ax.tick_params(axis='x', pad=0)
ax.tick_params(axis='y', pad=0)
ax.set_zlim(0, 1400)
cx = 15
cy = -15
ax.plot([cx], [cy], marker='x', markersize=10, color='black')
ax.text(-20,20,800, f"$lambda={lmbda:.1f}$", fontsize=10)
beta0 = np.linspace(-30, 30, 300)
beta1 = np.linspace(-30, 30, 300)
B0, B1 = np.meshgrid(beta0, beta1)
if mode=='L2':
Z1 = loss(B0, B1, a=1, b=1, c=0, cx=0, cy=0, lmbda=lmbda, yintercept=0)
Z2 = loss(B0, B1, a=5, b=5, c=0, cx=cx, cy=cy, yintercept=0)
Z = Z1 + Z2
elif mode=='L1':
Z1 = loss_l1(B0,B1,a=5,b=5,cx=0,cy=0,lmbda=lmbda)
Z2 = loss(B0, B1, a=5, b=5, c=0, cx=cx, cy=cy, yintercept=0)
Z = Z1 + Z2
origin = Circle(xy=(0, 0), radius=1, color='k')
ax.add_patch(origin)
art3d.pathpatch_2d_to_3d(origin, z=0, zdir="z")
scale = 1.5
vmax = 8000
contr = ax.contour(B0, B1, Z, levels=50, linewidths=.5,
cmap='coolwarm',
zdir='z', offset=0, vmax=vmax)
#surface plot
j = lmbda*scale
b0 = (j, 20-j)
beta0 = np.linspace(-j, 25-j, 300)
beta1 = np.linspace(-25+j, j, 300)
B0, B1 = np.meshgrid(beta0, beta1)
if mode=='L1':
Z1 = loss_l1(B0,B1,a=5,b=5,cx=0,cy=0,lmbda=lmbda)
Z2 = loss(B0, B1, a=5, b=5, c=0, cx=cx, cy=cy, yintercept=0)
Z = Z1 + Z2
elif mode=='L2':
Z1 = loss(B0, B1, a=1, b=1, c=0, cx=0, cy=0, lmbda=lmbda, yintercept=0)
Z2 = loss(B0, B1, a=5, b=5, c=0, cx=cx, cy=cy, yintercept=0)
Z = Z1 + Z2
vmax = 2700
ax.plot_surface(B0, B1, Z, alpha=1.0, cmap='coolwarm', vmax=vmax)
if mode=="L1":
boundary = diamond(lmbda=lmbda)
ax.plot(boundary[:, 0], boundary[:, 1], '-', lw=.5, c="red")
elif mode=="L2":
boundary = circle(lmbda=lmbda)
ax.plot(boundary[:, 0], boundary[:, 1], '-', lw=.5, c="red")
ax.view_init(elev=38, azim=-134)
plt.tight_layout()
last_lmbda = 10
stepsize = 3.0
lmbdas = list(np.arange(1, last_lmbda, step=stepsize))
for mode in ["L1", "L2"]:
plot_3d(mode, last_lmbda, stepsize, lmbdas)
References