Apa itu Regresi K-Nearest Neighbors (KNN)

Regresi K-Nearest Neighbors (KNN) adalah algoritma pembelajaran terawasi non-parametrik yang digunakan untuk memprediksi variabel target yang kontinu. Berbeda dengan model parametrik, Regresi KNN tidak membuat asumsi tentang distribusi data atau hubungan antar variabel. Sebaliknya, algoritma ini memperkirakan variabel target dengan mengambil rata-rata dari observasi yang berdekatan, di mana kedekatan diukur dengan metrik jarak. Regresi KNN adalah algoritma sederhana namun kuat yang dapat memodelkan hubungan non-linear dan kompleks.

Memilih Nilai 'K' yang Tepat

Pemilihan nilai 'K' merupakan faktor penting yang mempengaruhi kinerja algoritma KNN. Nilai yang lebih kecil untuk 'K' dapat menghasilkan model yang lebih kompleks yang menangkap pola lokal dalam data, namun dapat sensitif terhadap noise dan mengakibatkan overfitting. Di sisi lain, nilai yang lebih besar untuk 'K' dapat menghasilkan model yang lebih umum yang kurang sensitif terhadap noise, namun dapat mengabaikan pola lokal yang penting dan mengakibatkan underfitting. Memilih nilai 'K' yang tepat dapat dicapai melalui cross validation dan eksperimen.

Perbandingan dengan Regresi Linier

Berikut adalah perbedaan kunci antara regresi linier dan regresi KNN.

• Asumsi Model
  Regresi linier mengasumsikan bahwa ada hubungan linear antara variabel independen dan dependen, dan mencoba untuk menemukan garis lurus yang paling sesuai melalui titik data. Regresi KNN, di sisi lain, adalah metode non-parametrik, yang berarti tidak membuat asumsi tentang distribusi data atau hubungan antar variabel. Hal ini membuat regresi KNN lebih fleksibel dan mampu memodelkan hubungan non-linear dan kompleks.

• Kompleksitas Model
  Regresi linier menghasilkan model yang sederhana dan dapat diinterpretasikan yang direpresentasikan oleh garis lurus (atau hiperruang dalam kasus beberapa variabel independen). Regresi KNN dapat menghasilkan model yang lebih kompleks tergantung pada pilihan 'K' dan metrik jarak yang digunakan. Meskipun fleksibilitas ini dapat menguntungkan dalam situasi tertentu, ini juga dapat membuat model lebih rentan terhadap overfitting, terutama dengan nilai 'K' yang kecil.

• Skala Fitur
  Regresi linier kurang sensitif terhadap skala fitur, karena memperkirakan koefisien untuk setiap fitur secara independen. Namun, regresi KNN bergantung pada metrik jarak untuk menemukan tetangga terdekat, yang membuatnya sensitif terhadap skala fitur. Oleh karena itu, scaling fitur (misalnya, normalisasi atau standarisasi) adalah langkah preprocessing yang penting dalam Regresi KNN.

• Waktu Pelatihan dan Prediksi
  Regresi linier memiliki solusi bentuk tertutup yang dapat dihitung dengan efisien, membuat proses pelatihan relatif cepat. Begitu koefisien diestimasi, prediksi juga dapat dilakukan dengan cepat. Sebaliknya, Regresi KNN tidak memiliki fase pelatihan yang eksplisit, karena menyimpan seluruh kumpulan data pelatihan untuk membuat prediksi. Akibatnya, waktu prediksi untuk Regresi KNN bisa jauh lebih lambat, terutama untuk kumpulan data besar.

• Penanganan Outlier
  Regresi linier sensitif terhadap outlier dalam data, karena mereka dapat memiliki dampak yang signifikan pada koefisien yang diestimasi dan, oleh karena itu, kinerja model. Regresi KNN, dengan pilihan 'K' yang tepat, umumnya lebih tahan terhadap outlier, karena mempertimbangkan beberapa titik tetangga saat membuat prediksi.

Menerapkan Regresi KNN dengan Python

Di bab ini, saya akan menunjukkan bagaimana mengimplementasikan Regresi KNN dalam Python menggunakan kumpulan data Perumahan California. Kita juga akan mengeksplorasi efek variasi nilai 'K' dan memilih nilai 'K' terbaik melalui cross validation.

Pertama, mari impor pustaka yang diperlukan:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasets
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error

Selanjutnya, mari muat kumpulan data Perumahan California dan lakukan preprocessing dasar:

# Load the California Housing dataset
california_housing = datasets.fetch_california_housing()
X = california_housing.data
y = california_housing.target

# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Scale the features
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

Selanjutnya, kita akan mengimplementasikan model Regresi KNN dan mengevaluasi kinerjanya menggunakan cross validation:

# Initialize a range of K values
k_values = np.arange(1, 31)

# Perform GridSearchCV to find the best K value
knn_regressor = KNeighborsRegressor()
param_grid = {'n_neighbors': k_values}
grid_search = GridSearchCV(knn_regressor, param_grid, cv=5, scoring='neg_mean_squared_error', n_jobs=-1)
grid_search.fit(X_train_scaled, y_train)

# Obtain the best K value and corresponding performance
best_k = grid_search.best_params_['n_neighbors']
best_performance = -grid_search.best_score_
print(f"Best K value: {best_k}")
print(f"Best performance (Mean Squared Error): {best_performance}")

Sekarang, mari buat plot yang keren dan informatif menunjukkan kinerja Regresi KNN dengan berbagai nilai K:

# Retrieve the performance for each K value
performance = -grid_search.cv_results_['mean_test_score']

# Set up the plotting environment
sns.set(style="darkgrid")
plt.figure(figsize=(10, 6))

# Plot the performance for each K value
plt.plot(k_values, performance, marker='o', linestyle='-', linewidth=2)
plt.xlabel("Number of Neighbors (K)")
plt.ylabel("Mean Squared Error")
plt.title("KNN Regression Performance with Various K")

# Highlight the best K value
plt.scatter(best_k, best_performance, s=200, c='red', marker='x', zorder=5)
plt.annotate(f"Best K: {best_k}",
             xy=(best_k, best_performance),
             xytext=(best_k + 2, best_performance),
             arrowprops=dict(facecolor='black', arrowstyle='->'))

plt.show()

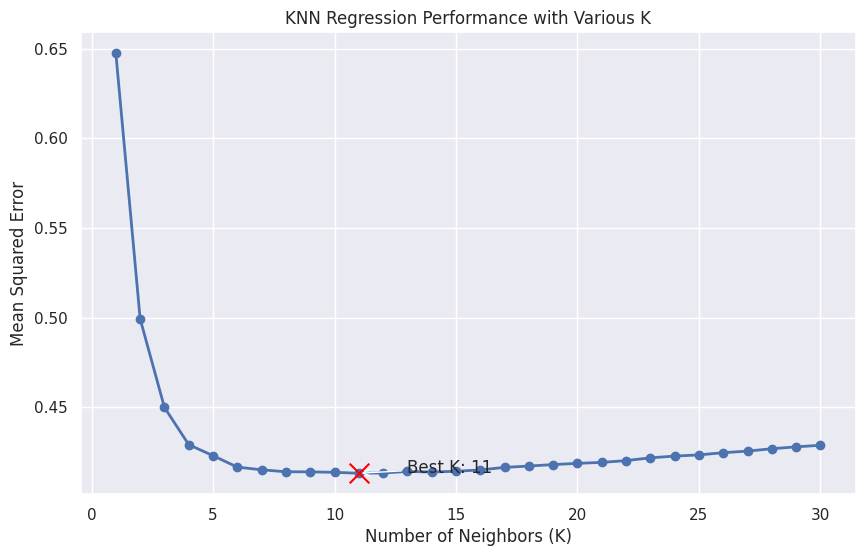
Grafik ini menunjukkan kinerja Regresi KNN untuk nilai K yang berbeda, dengan nilai K terbaik disorot dalam warna merah. Grafik harus membantu Anda memvisualisasikan trade-off antara overfitting dan underfitting saat K bervariasi, sehingga lebih mudah untuk memilih nilai optimal untuk model Anda.

Untuk memplot prediksi Regresi KNN dengan berbagai nilai K, kita akan memilih satu fitur dari kumpulan data Perumahan California untuk tujuan visualisasi. Kita akan menggunakan fitur 'MedInc' (Pendapatan Median), yang merupakan kolom pertama dalam kumpulan data. Kemudian, kita akan membuat scatterplot nilai target aktual dan overlay prediksi Regresi KNN untuk nilai K yang berbeda.

# Extract the 'MedInc' feature for visualization
X_medinc = X_train_scaled[:, 0].reshape(-1, 1)

# Generate a range of 'MedInc' values for plotting
medinc_range = np.linspace(X_medinc.min(), X_medinc.max(), 100).reshape(-1, 1)

# Set up the plotting environment
sns.set(style="darkgrid")
plt.figure(figsize=(12, 8))

# Create a scatterplot of the actual target values
plt.scatter(X_medinc, y_train, s=15, c='gray', label='Actual Data')

# Overlay the KNN Regression predictions for various K values
k_values_to_plot = [1, 5, 10, 20, best_k]
colors = ['red', 'blue', 'green', 'purple', 'orange']
for k, color in zip(k_values_to_plot, colors):
    knn_regressor = KNeighborsRegressor(n_neighbors=k)
    knn_regressor.fit(X_medinc, y_train)
    predictions = knn_regressor.predict(medinc_range)
    plt.plot(medinc_range, predictions, linestyle='-', color=color, label=f'K={k}')

# Customize the plot appearance
plt.xlabel("Median Income (Normalized)")
plt.ylabel("Median House Value")
plt.title("KNN Regression with Various K")
plt.legend()
plt.show()

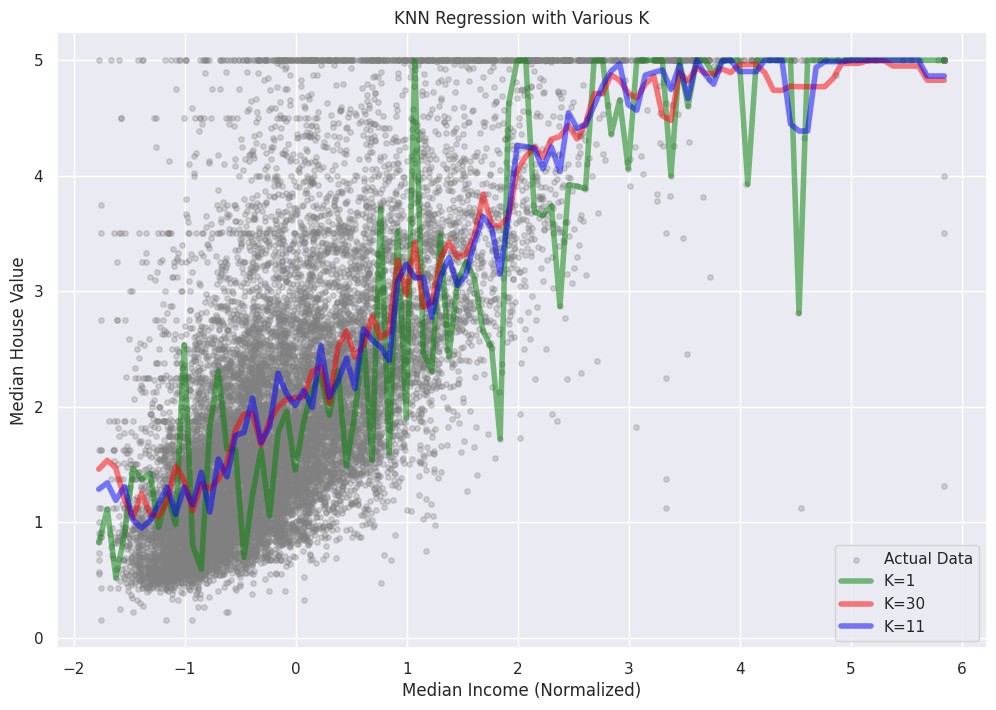
Dalam plot ini, kita dapat melihat bagaimana prediksi Regresi KNN berubah untuk nilai K yang berbeda. Ketika K meningkat, model menjadi lebih halus dan kurang sensitif terhadap titik data individu, mengurangi risiko overfitting. Namun, penting untuk memilih nilai K yang sesuai untuk menemukan keseimbangan antara menangkap pola-pola yang mendasar di dalam data dan menghindari overfitting atau underfitting.

Referensi

https://bookdown.org/tpinto_home/Regression-and-Classification/k-nearest-neighbours-regression.html
https://www.youtube.com/watch?v=HVXime0nQeI&ab_channel=StatQuestwithJoshStarmer