Apa itu distribusi multinomial
Distribusi multinomial adalah distribusi probabilitas yang mengikuti probabilitas
Distribusi multinomial adalah distribusi probabilitas yang memperluas distribusi binomial ke dimensi
Ketika
Probabilitas dari distribusi multinomial dinyatakan dengan persamaan berikut:
Distribusi multinomial kadang-kadang dilambangkan sebagai
Nilai yang diharapkan dan varians dari distribusi multinomial
Nilai yang diharapkan dan varians dari distribusi kategorikal masing-masing adalah:
Periksa efek dari $N
Dengan
import numpy as np
from scipy.stats import multinomial
import matplotlib
import matplotlib.pyplot as plt
from matplotlib import animation, rc
from matplotlib.animation import FuncAnimation
rc('animation', html='html5')
np.random.seed(5)
# Set up formatting for the movie files
Writer = animation.writers['ffmpeg']
writer = Writer(fps=15, metadata=dict(artist='Me'), bitrate=1800)
p_v = np.array([0.2, 0.3, 0.5])
N_max = 20
p_max = 0.1
plt.style.use('ggplot')
cm = plt.get_cmap('jet')
fig = plt.figure(figsize=(10, 5))
ax = fig.add_subplot(projection='3d')
def update(N):
# initialize previous frame
plt.cla()
N += 1
x_vals = np.arange(N + 1)
X1, X2 = np.meshgrid(x_vals, x_vals)
x1_vals = np.delete(X1.flatten(), obj=(X1 + X2).flatten() > N)
x2_vals = np.delete(X2.flatten(), obj=(X1 + X2).flatten() > N)
x3_vals = np.where(x1_vals+x2_vals <= N, N - (x1_vals+x2_vals), 0.0)
x_points = np.stack([x1_vals, x2_vals, x3_vals], axis=1)
probability = multinomial.pmf(x=x_points, n=N, p=p_v)
ax.bar3d(x=x1_vals - 0.45,
y=x2_vals - 0.45,
z=np.zeros_like(x1_vals),
dx=0.9,
dy=0.9,
dz=probability,
color=cm(probability / p_max),
alpha=0.5,
shade=True
)
ax.set_xlabel('$x_1$')
ax.set_ylabel('$x_2$')
ax.set_zlabel('Probability')
ax.set_title('$p=(' + ', '.join([str(phi) for phi in p_v]) + ')' +
', N=' + str(N) + '$', loc='left')
ax.set_zlim(0.0, p_max)
anime_prob = FuncAnimation(fig, update, frames=N_max, interval=100)
anime_prob.save('multinomial_dist.gif', writer='pillow', fps=1)
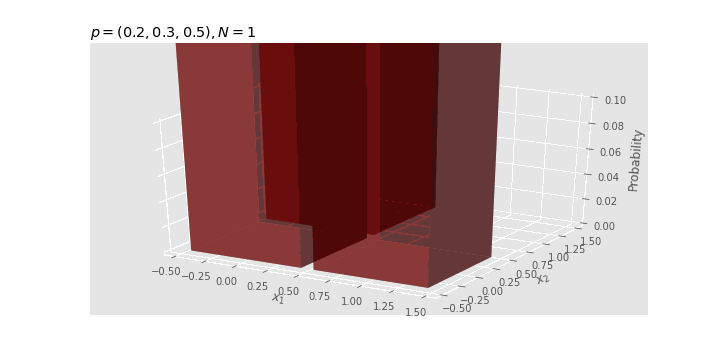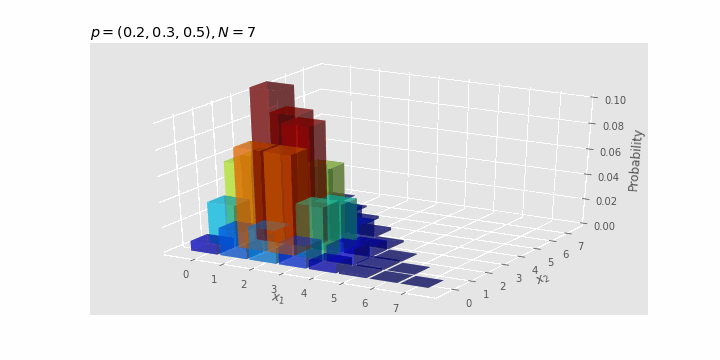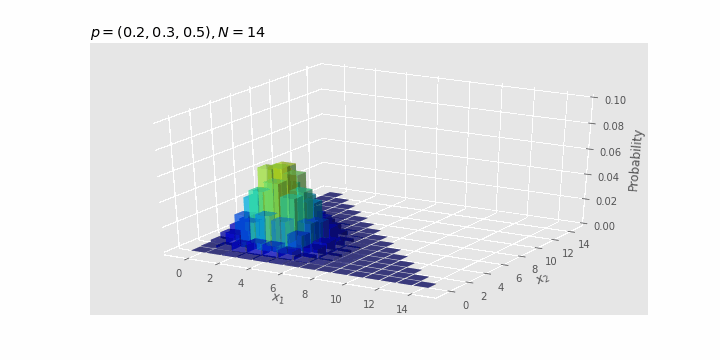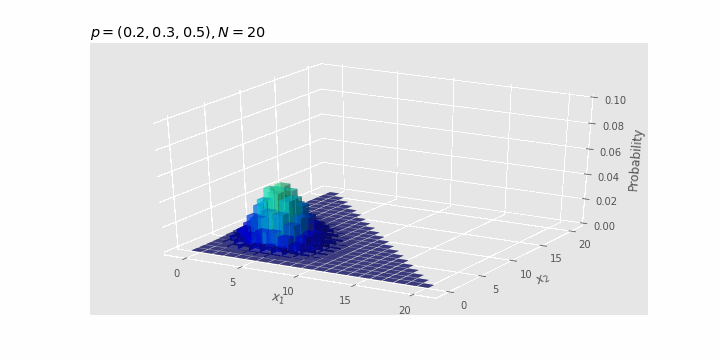
Seiring dengan bertambahnya