2022-12-23

Regresi logistik

Statistics

Statistical Model

Python

Apa itu regresi logistik

Regresi logistik adalah GLM yang digunakan untuk mengekspresikan kejadian yang diamati dalam hal distribusi binomial.

fungsi link dari distribusi binomial sering kali merupakan fungsi link logit, yang sesuai dengan sisi kiri dari persamaan berikut.

\log \frac{p_i}{1-p_i}=z_i

di mana $p_i$ adalah probabilitas dan $z_i$ adalah prediktor linier.

Membangun model regresi logistik

Mari kita benar-benar membangun model regresi logistik. Di sini kita mempertimbangkan data benih untuk 100 tanaman fiktif. Data terdiri dari kolom-kolom berikut ini:

N: Jumlah benih
y: Jumlah benih yang berkecambah
x: Ukuran individu
f: Apakah individu-individu tersebut diberi pupuk atau tidak (C: tidak diberi pupuk, T: diberi pupuk)

import pandas as pd

# number of seeds
N = [8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,
     8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,
     8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8]

# number of seeds germinated
y = [1,6,5,6,1,1,3,6,0,8,0,2,0,5,3,6,3,4,5,8,5,8,1,4,1,8,4,7,5,5,8,1,7,1,3,8,6,7,
     7,4,7,8,8,0,6,5,8,3,8,8,0,5,5,8,3,2,7,8,3,5,8,3,6,7,8,6,5,5,0,8,8,0,6,1,8,8,
     6,6,6,6,8,8,7,8,6,2,0,7,8,8,8,3,7,8,8,7,0,5,8,1]

# body size
x = [9.76,10.48,10.83,10.94,9.37,8.81,9.49,11.02,7.97,11.55,9.46,9.47,8.71,10.42,10.06,
     11,9.95,9.52,10.26,11.33,9.77,10.59,9.35,10,9.53,12.06,9.68,11.32,10.48,10.37,11.33,
     9.42,10.68,7.91,9.39,11.65,10.66,11.23,10.57,10.42,11.73,12.02,11.55,8.58,11.08,10.49,
     11.12,8.99,10.08,10.8,7.83,8.88,9.74,9.98,8.46,7.96,9.78,11.93,9.04,10.14,11.01,8.88,
     9.68,9.8,10.76,9.81,8.37,9.38,7.68,10.23,9.83,7.66,9.33,8.2,9.54,10.55,9.88,9.34,10.38,
     9.63,12.44,10.17,9.29,11.17,9.13,8.79,8.19,10.25,11.3,10.84,10.97,8.6,9.91,11.38,10.39,
     10.45,8.94,8.94,10.14,8.5]

# feed (C: control, T: treatment)
f = ['C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C',
     'C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C',
     'C','C','C','C','C','C','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T',
     'T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T',
     'T','T','T','T','T','T','T','T','T','T','T','T']

df = pd.DataFrame(list(zip(N, y, x, f)), columns =['N', 'y', 'x', 'f'])
display(df.head())

	N	y	x	f
0	8	1	9.76	C
1	8	6	10.48	C
2	8	5	10.83	C
3	8	6	10.94	C
4	8	1	9.37	C

Investigasi data

Mari kita periksa statistik deskriptif.

df.describe()

	N	y	x
count	100.0	100.000000	100.000000
mean	8.0	5.080000	9.967200
std	0.0	2.743882	1.088954
min	8.0	0.000000	7.660000
25%	8.0	3.000000	9.337500
50%	8.0	6.000000	9.965000
75%	8.0	8.000000	10.770000
max	8.0	8.000000	12.440000

Menampilkan jumlah C dan T untuk f, masing-masing.

print('num of C:', len(df[df['f'] == 'C']))
print('num of T:', len(df[df['f'] == 'T']))

num of C: 50
num of T: 50

Statistik deskriptif dari data mengkonfirmasi hal-hal berikut ini

Jumlah benih N:
- Semua angka dalam 8.
Jumlah benih yang berkecambah y:
- Bilangan bulat non-negatif (0 sampai 8)
Ukuran individu x:
- Bilangan real positif (nilai kontinu)
- Varians kecil.
Perlakuan pupuk f:
- Ini adalah data kategorikal.
- Jumlah elemen dalam setiap kategori adalah sama.

import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

plt.style.use('ggplot')
plt.figure(figsize=(10,5))
sns.set(rc={'figure.figsize':(10,5)})

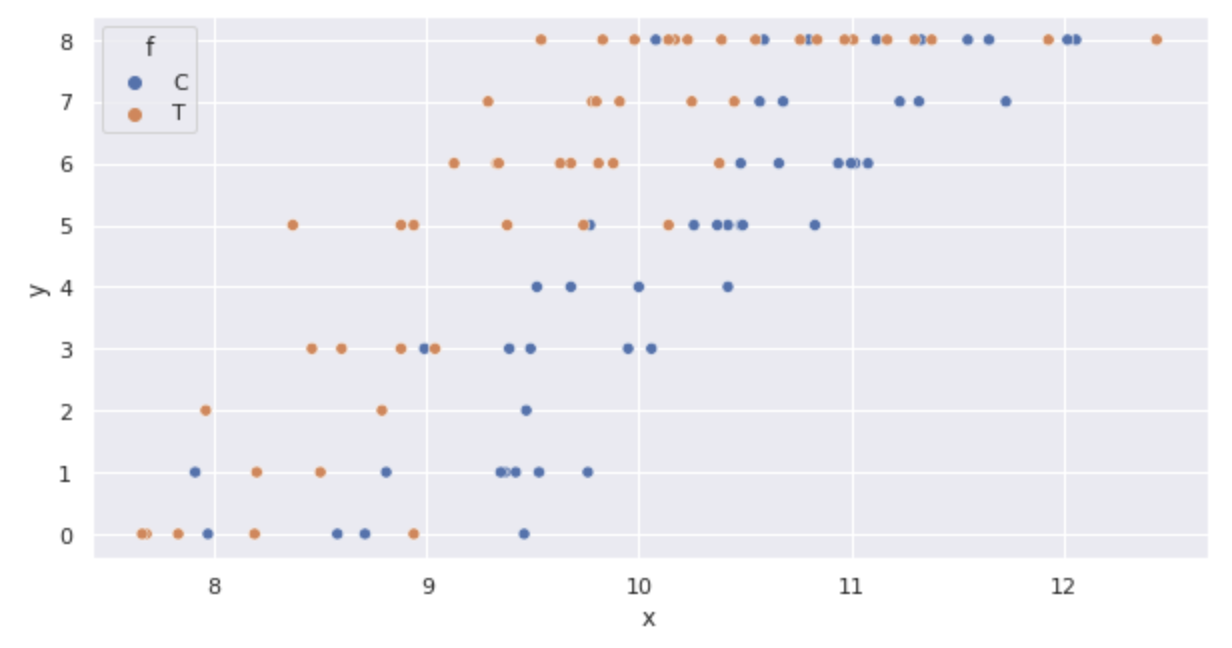
sns.scatterplot(x='x', y='y', hue='f', data=df)

Scatter of f

Menampilkan diagram kotak-dan-whisker.

sns.boxplot(x='f', y='y', data=df)

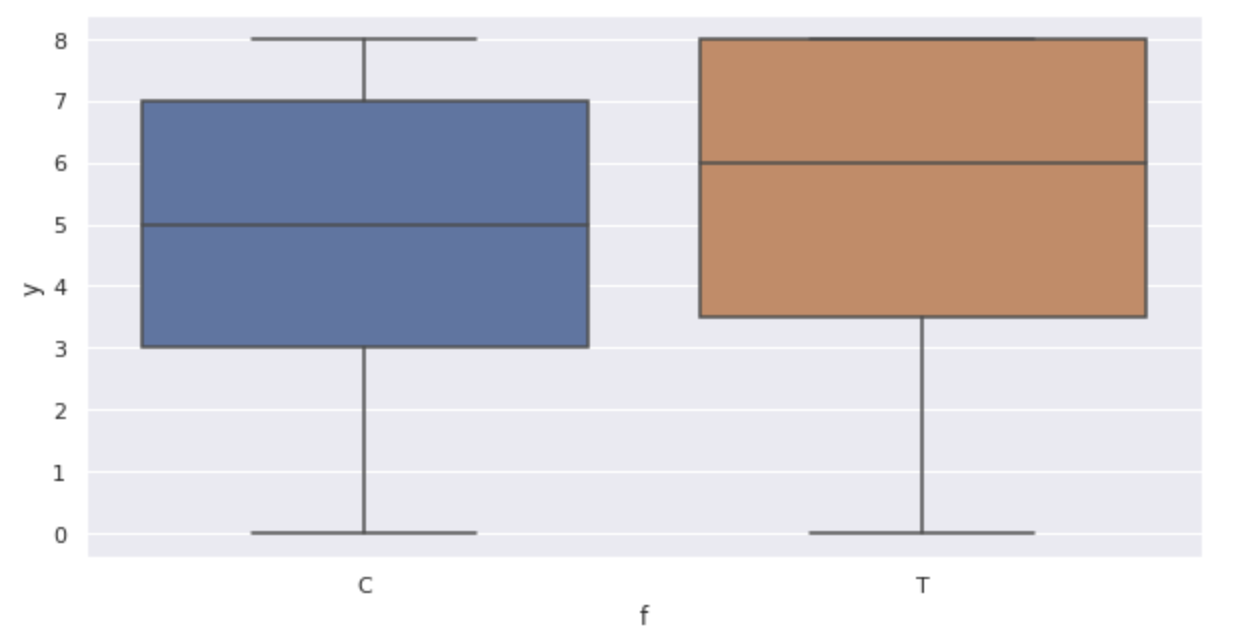
Box of f

Grafik tersebut menegaskan hal berikut ini:

Seiring dengan meningkatnya ukuran $x$ , jumlah benih yang berkecambah y juga meningkat (scatter plot).
Jumlah benih yang berkecambah y juga meningkat seiring dengan pemupukan (plot kotak-dan-whisker)

Pembuatan Model

Untuk data $N$ dan $y$ , kita dapat mengasumsikan bahwa $N=8$ benih diekstraksi, $y$ dari 8 benih berkecambah, dan $8-y$ benih tidak berkecambah. Distribusi probabilitas yang sering digunakan untuk kejadian seperti itu adalah distribusi binomial.

Distribusi binomial diwakili oleh persamaan berikut:

P(X = y) = \frac{N!}{y!(N-y)!}p^{y}(1-p)^{N-y}

Biarkan $p$ menjadi probabilitas perkecambahan.

Kita mempertimbangkan model statistik di mana probabilitas perkecambahan $p_i$ dari individu $i$ diekspresikan dalam hal ukuran $x_i$ dan perlakuan pemupukan $f_i$ .

P(X = y_i) = \frac{N!}{y_i!(N-y_i)!}p^{y_i}(1-p_i)^{N-y_i}

Fungsi yang sering digunakan untuk mengekspresikan probabilitas adalah fungsi logistik. Fungsi logistik dinyatakan dengan persamaan berikut:

y = \frac{1}{1 + e^{-x}}

Fungsi logistik diilustrasikan di bawah ini.

import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
%matplotlib inline

plt.style.use('ggplot')
plt.figure(figsize=(10,5))

x = np.arange(-10, 10, 0.01)
y = [ 1 / ( 1 + math.exp(-x_i))  for x_i in x]
plt.plot(x, y, color='black', label='logsitic function')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()

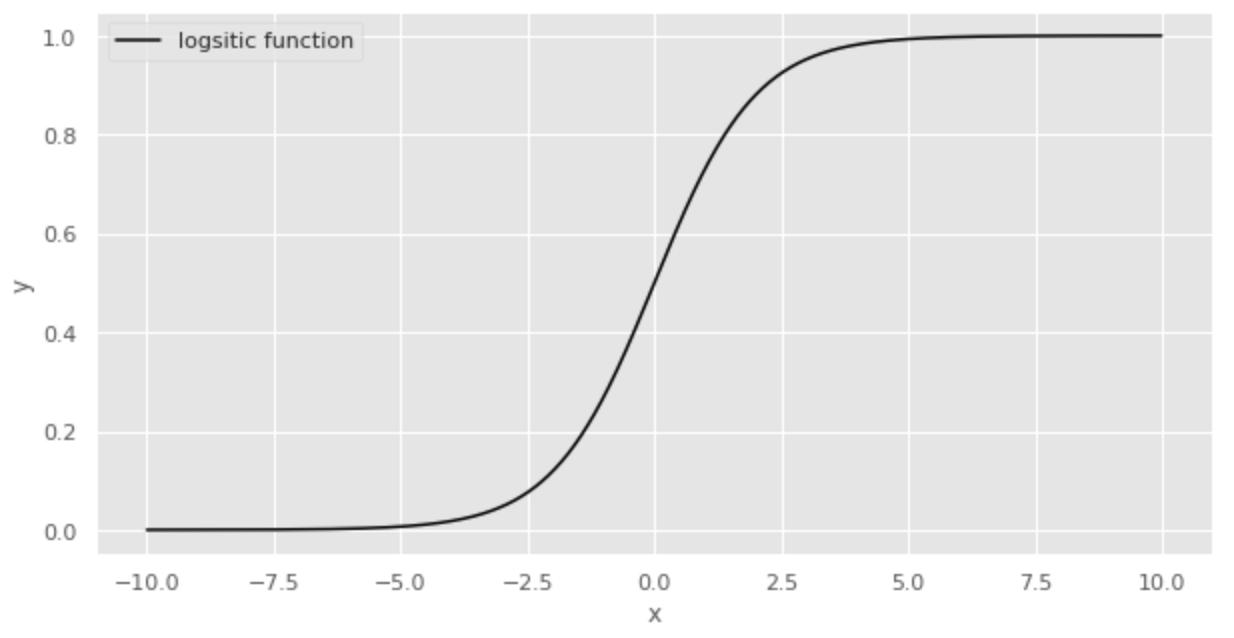
Logistic function

Fungsi logistik berkisar dari 0 sampai 1 untuk y dan 0,5 ketika x adalah 0. Sifat ini membuat fungsi logistik menjadi fungsi yang cocok untuk mengekspresikan probabilitas.

Jika kita mengganti fungsi logistik dengan variabel-variabel dalam kasus ini, kita mendapatkan persamaan berikut.

p_i = \frac{1}{1 + e^{-z_i}}

di mana $z_i$ adalah prediktor linier.

Transformasi untuk $z_i$ adalah sebagai berikut.

\log \frac{p_i}{1-p_i}=z_i

Sisi kiri dari persamaan di atas disebut fungsi link logit. Fungsi logit link adalah fungsi kebalikan dari fungsi logistik.

Mengekspresikan probabilitas perkecambahan benih $p_i$ dalam hal ukuran $x$ dan dengan/tanpa perlakuan pemupukan $d$ (variabel dummy untuk perlakuan pemupukan $f$ ), $z_i$ adalah sebagai berikut:

z_i = \beta_1 + \beta_2 x_i + \beta_3 d_i

Artinya, probabilitas perkecambahan $p_i$ adalah sebagai berikut:

p_i = \frac{1}{1 + e^{\beta_1 + \beta_2 x_i + \beta_3 d_i}}

Oleh karena itu, kita mencari $\beta_1$ , $\beta_2$ , dan $\beta_3$ yang memaksimalkan fungsi log-likelihood berikut:

L(p_i) = \prod^{100}_{i=1} \frac{N!}{y_i!(N-y_i)!}p^{y_i}(1-p_i)^{N-y_i}

Estimasi parameter

$\beta_1$ , $\beta_2$ , dan $\beta_3$ dapat dengan mudah diestimasi dengan kode berikut.

import statsmodels.api as sm
import statsmodels.formula.api as smf

fit_xf = smf.glm(formula='y + I(N - y) ~ x + f', data=df, family=sm.families.Binomial()).fit()
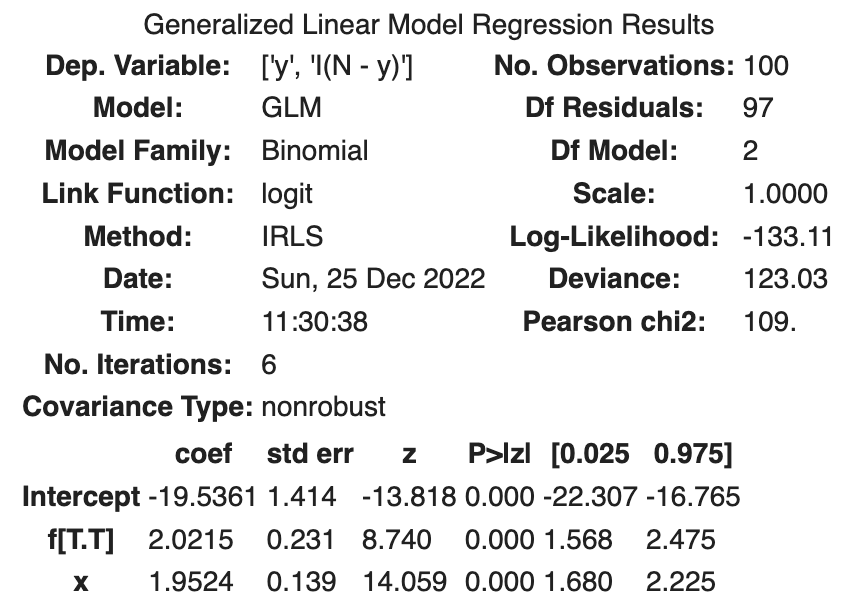
fit_xf.summary()

Poisson regression | f

# aic
fit_xf.aic

Hasil berikut ini diperoleh.

	coef	std err	z	Log-likelihood	AIC
Intercept	-19.5361	1.414	-13.818
f[T.T]	2.0215	0.231	8.740
x	1.9524	0.139	14.059
				-133.11	272.21

Substitusikan estimasi parameter ke dalam model regresi logistik dan ilustrasikan.

import numpy as np
import math

sns.scatterplot(x='x', y='y', hue='f', data=df)
x = np.arange(df.x.min(), df.x.max() + 0.01, 0.01)
y_T = [8 * 1 / ( 1 + math.exp(-(fit_xf.params['Intercept'] + fit_xf.params['x'] * x_i + fit_xf.params['f[T.T]'])))  for x_i in x]
y_C = [8 * 1 / ( 1 + math.exp(-(fit_xf.params['Intercept'] + fit_xf.params['x'] * x_i)))  for x_i in x]
plt.plot(x, y_T, color='black', label='logsitic T')
plt.plot(x, y_C, color='gray', label='logsitic C')
plt.legend()
plt.show()

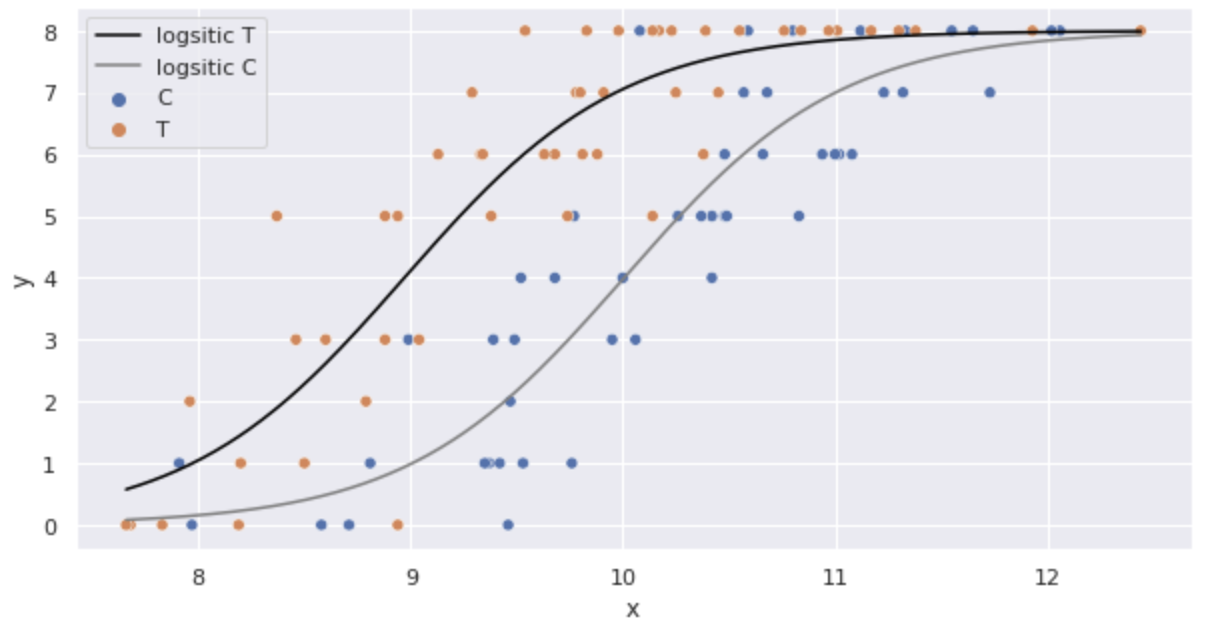
logistic regression

Sepertinya model yang baik sedang dibangun.

Menginterpretasikan logit

Mari kita transformasikan fungsi link logit sebagai berikut:

\log \frac{p_i}{1 - p_i} = z_i = \beta_1 + \beta_2 x_i + \beta_3 d_i

\frac{p_i}{1 - p_i} = e^{\beta_1 + \beta_2 x_i + \beta_3 d_i} = e^{\beta_1} e^{\beta_2 x_i} e^{\beta_3 d_i}

Sisi kiri $\frac{p_i}{1 - p_i}$ adalah nilai yang disebut odds, yang dalam hal ini dapat diartikan sebagai (probabilitas perkecambahan)/(probabilitas tidak berkecambah). Sebagai contoh, jika $p_i=0.5$ , peluangnya adalah 1x.

Peluangnya sebanding dengan $e^{\textrm{parameter} \times \textrm{factor}}$ . Peluang untuk ada atau tidaknya perlakuan pupuk adalah sebagai berikut