2022-12-23

Model campuran linier umum

Apa itu Model Campuran linier Tergeneralisasi (GLMM)

Model Campuran linier Tergeneralisasi (Generalized Linear Mixed Model: GLMM) adalah model statistik yang merupakan pengembangan lebih lanjut dari GLM. Model ini dapat mewakili perbedaan individu dan regional yang tidak dapat diamati.

Perbedaan individu dan regional yang tidak dapat diamati termasuk, misalnya, berikut ini:

Perbedaan individu dalam persepsi nyeri
Orang yang berbeda merespons secara berbeda terhadap nyeri yang sama.
Perbedaan individu dalam penilaian
Beberapa penilai lebih lunak daripada yang lain.
Perbedaan regional
Ada variasi regional dalam sifat nyeri.

Sebuah model yang tidak memperhitungkan perbedaan individu dan regional ini akan menyebabkan overdispersi. Overdispersi berarti bahwa distribusi probabilitas yang diasumsikan memiliki varians yang lebih besar daripada yang diasumsikan. Gambar berikut ini menunjukkan overdispersi dengan menggunakan distribusi Poisson sebagai contoh.

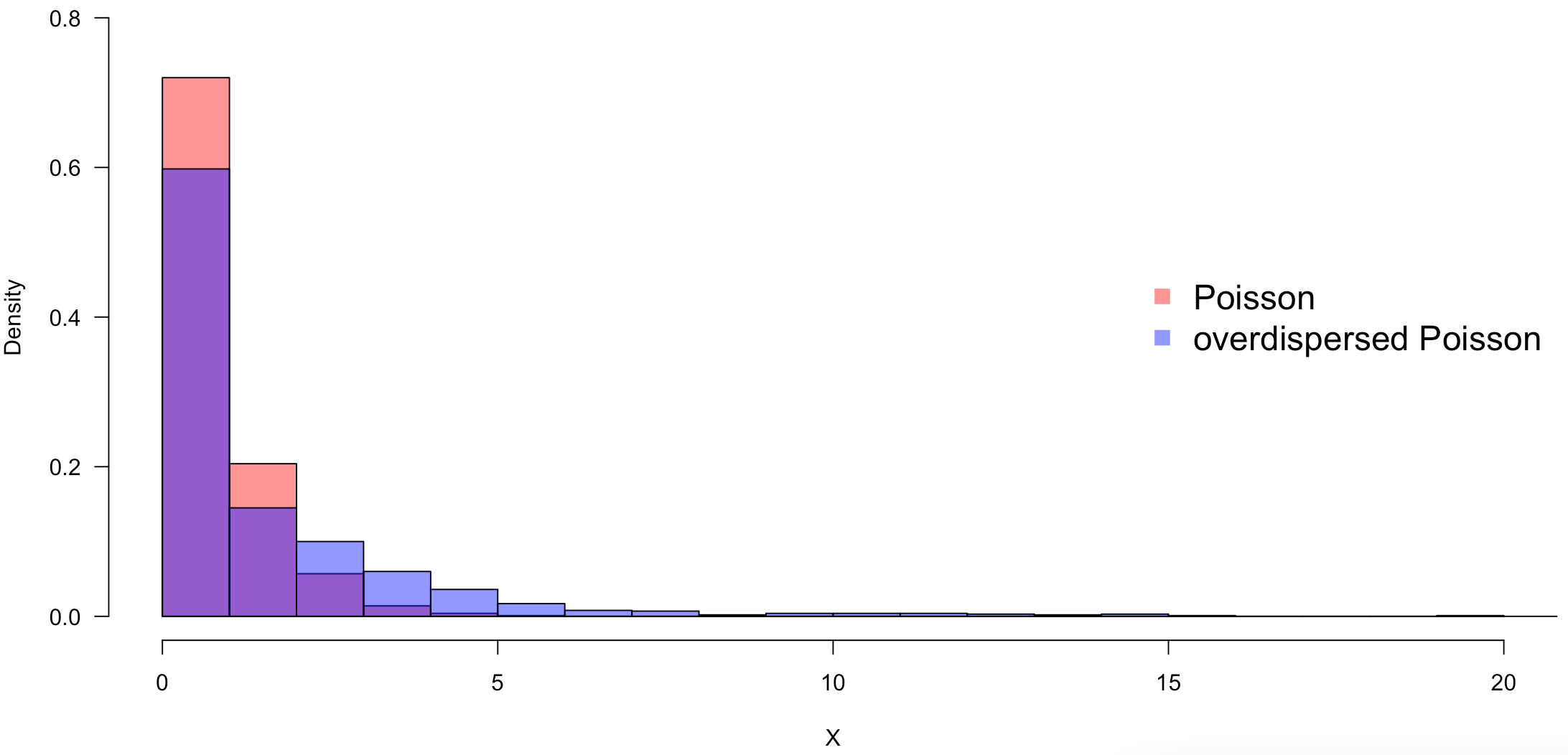
Overdispersion

Perbedaan individu dan wilayah dapat menghasilkan distribusi Poisson yang lebih besar dari distribusi Poisson asli, seperti dalam kasus overdispersed Poisson, dan tanpa memperhitungkan perbedaan individu dan lokasi, data yang diamati tidak dapat dimodelkan dengan baik.

GLMM memperlakukan variasi yang tidak dapat dijelaskan seperti perbedaan individu dan lokasi sebagai efek acak dan memodelkannya seperti itu, dengan menentukan bahwa tidak mungkin untuk mengamati semua variabel penjelas.

Efek Acak

GLMM menambahkan efek acak ke prediktor linier. Misalnya, untuk individu $i$ , tambahkan perbedaan individu sebagai efek acak $\eta_i$ sebagai berikut:

g(y_i) = \beta_1 + \beta_2 x_i + \cdots + \eta_i

Kita asumsikan bahwa efek acak $\eta_i$ mengikuti distribusi normal dengan mean 0 dan varians $s$ . Tidak ada alasan untuk mengasumsikan bahwa distribusi $\eta_i$ mengikuti distribusi normal, tetapi diasumsikan sebagai distribusi normal karena akan lebih mudah untuk pemodelan statistik.

Estimasi maksimum likelihood dari parameter akan dilakukan untuk $\beta$ dan $s$ .

Kasus-kasus di mana GLMM diperlukan

Kriteria untuk menentukan apakah GLMM diperlukan adalah apakah Anda mengambil sampel individu atau lokasi yang sama berulang-ulang. Sebagai contoh, GLMM sering diterapkan pada data panel, yaitu data yang diamati berulang kali dari waktu ke waktu untuk individu.

Membangun GLMM

Mari kita membangun GLMM menggunakan dataset grouseticks. grouseticks adalah pengamatan jumlah kutu di kepala anak ayam belibis merah dan terdiri dari kolom-kolom berikut:

INDEX: (factor) chick number (observation level)
TICKS: number of ticks sampled
BROOD: (factor) brood number
HEIGHT: height above sea level (meters)
YEAR: year (-1900)
LOCATION: (factor) geographic location code
cHEIGHT: centered height, derived from HEIGHT

Mari kita periksa data.

> require(lme4)
> library(lme4)
> data(grouseticks)
> summary(grouseticks)

    INDEX         TICKS           BROOD         HEIGHT      YEAR        LOCATION      cHEIGHT
1      :  1   Min.   : 0.00   606    : 10   Min.   :403.0   95:117   14     : 24   Min.   :-59.241
2      :  1   1st Qu.: 0.00   602    :  9   1st Qu.:430.0   96:155   4      : 20   1st Qu.:-32.241
3      :  1   Median : 2.00   537    :  7   Median :457.0   97:131   19     : 20   Median : -5.241
4      :  1   Mean   : 6.37   601    :  7   Mean   :462.2            28     : 19   Mean   :  0.000
5      :  1   3rd Qu.: 6.00   643    :  7   3rd Qu.:494.0            50     : 17   3rd Qu.: 31.759
6      :  1   Max.   :85.00   711    :  7   Max.   :533.0            36     : 16   Max.   : 70.759
(Other):397                   (Other):356                            (Other):287

> head(grouseticks)

  INDEX TICKS BROOD HEIGHT YEAR LOCATION   cHEIGHT
1     1     0   501    465   95       32  2.759305
2     2     0   501    465   95       32  2.759305
3     3     0   502    472   95       36  9.759305
4     4     0   503    475   95       37 12.759305
5     5     0   503    475   95       37 12.759305
6     6     3   503    475   95       37 12.759305

> plot(TICKS ~ HEIGHT, las=1)

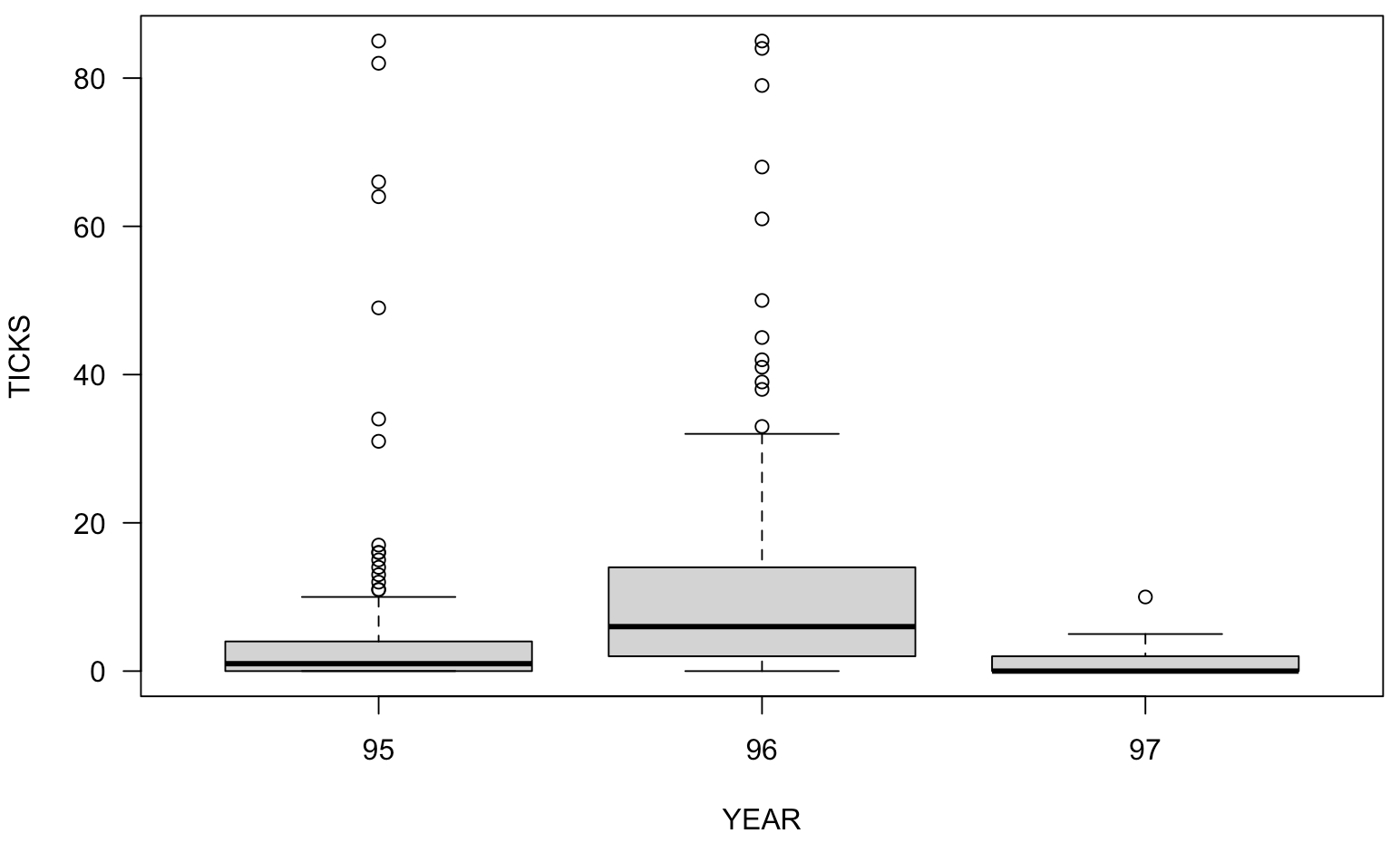
TICKS and HEIGHT

Regresi Poisson tanpa efek acak

Kali ini kita akan membangun model regresi Poisson. Dengan menggunakan rata-rata jumlah kutu $\lambda_i$ kita mengekspresikan fungsi log-link sebagai berikut

\log \lambda_i = \beta_1 + \beta_2 d_i

dimana $d_i$ adalah variabel dummy untuk YEAR.

Kode berikut dapat digunakan untuk mengestimasi parameter.

> fit_glm <- glm(TICKS ~ YEAR, family=poisson(), data=grouseticks)
> summary)(fit_glm)

Call:
glm(formula = TICKS ~ YEAR, family = poisson(), data = grouseticks)

Deviance Residuals:
    Min       1Q   Median       3Q      Max
-4.7110  -2.8888  -1.5183   0.7139  17.1467

Coefficients:
            Estimate Std. Error z value Pr(>|z|)
(Intercept)  1.78318    0.03790   47.05   <2e-16 ***
YEAR96       0.62348    0.04492   13.88   <2e-16 ***
YEAR97      -1.64109    0.08977  -18.28   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 5847.5  on 402  degrees of freedom
Residual deviance: 4549.4  on 400  degrees of freedom
AIC: 5486.4

Number of Fisher Scoring iterations: 6

AIC adalah 5486.4.

Regresi Poisson dengan efek acak

mari kita buat model regresi Poisson dengan efek acak.

Model intersep acak

Tambahkan efek acak $\eta_j$ dari lokasi $j$ dengan LOCATION dan nyatakan rata-rata jumlah kutu $\lambda_i$ sebagai berikut.

\log \lambda_i = \beta_1 + \beta_2 d_i + \eta_j, \quad \eta_j \sim N(0, s^2)

Model ini juga disebut model intersep acak karena efek acak dimasukkan dalam intersep.

Anda dapat mengestimasi $\beta$ dan $S$ dengan kode berikut. Jika Anda menginginkan efek acak dalam intersep, tulis TICKS ~ YEAR + (1 | LOCATION).

> fit_glmm <- glmer(TICKS ~ YEAR + (1 | LOCATION), family="poisson", data=grouseticks)
> summary(fit_glmm)

Generalized linear mixed model fit by maximum likelihood (Laplace Approximation) ['glmerMod']
 Family: poisson  ( log )
Formula: TICKS ~ YEAR + (1 | LOCATION)
   Data: grouseticks

     AIC      BIC   logLik deviance df.resid
  2306.3   2322.3  -1149.1   2298.3      399

Scaled residuals:
    Min      1Q  Median      3Q     Max
-6.6399 -0.8844 -0.4708  0.8543  5.5757

Random effects:
 Groups   Name        Variance Std.Dev.
 LOCATION (Intercept) 1.644    1.282
Number of obs: 403, groups:  LOCATION, 63

Fixed effects:
            Estimate Std. Error z value Pr(>|z|)
(Intercept)  0.64992    0.18319   3.548 0.000388 ***
YEAR96       0.94371    0.08492  11.113  < 2e-16 ***
YEAR97      -1.43642    0.12298 -11.681  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Correlation of Fixed Effects:
       (Intr) YEAR96
YEAR96 -0.295
YEAR97 -0.241  0.520

AIC sekarang 2306.3, peningkatan yang signifikan dibandingkan model tanpa efek acak.

Varians dari efek acak untuk LOCATION adalah 1.644. Anda dapat memeriksa efek acak dari semua LOCATION dengan fungsi randf().

> ranef(fit_glmm)

$LOCATION
   (Intercept)
1   1.24539318
2   0.92293852
3  -0.93190888
.
.
.
61 -1.35144088
62 -0.95446024
63 -1.15277383

with conditional variances for “LOCATION”

Nilai-nilai dari 1 sampai 63 adalah nilai LOCATION: intersep untuk 1 adalah 1.24539318 dan intersep untuk 3 adalah -0.93190888. Interpretasinya adalah bahwa LOCATION 1 relatif lebih banyak kutu daripada LOCATION 3.

Selain itu, efek acak $\tau_i$ karena INDEX dapat ditambahkan.

\log \lambda_i = \beta_1 + \beta_2 d_i + \eta_j + \tau_i, \quad \eta_j \sim N(0, s^2), \tau_i \sim N(0, \sigma^2)

> fit_glmm <- glmer(TICKS ~ YEAR + (1 | LOCATION) + (1 | INDEX), family="poisson", data=grouseticks)
> summary(fit_glmm)

Generalized linear mixed model fit by maximum likelihood (Laplace Approximation) ['glmerMod']
 Family: poisson  ( log )
Formula: TICKS ~ YEAR + (1 | LOCATION) + (1 | INDEX)
   Data: grouseticks

     AIC      BIC   logLik deviance df.resid
  1863.9   1883.9   -927.0   1853.9      398

Scaled residuals:
    Min      1Q  Median      3Q     Max
-1.5003 -0.5933 -0.1154  0.2723  2.3743

Random effects:
 Groups   Name        Variance Std.Dev.
 INDEX    (Intercept) 0.5081   0.7128
 LOCATION (Intercept) 1.4679   1.2116
Number of obs: 403, groups:  INDEX, 403; LOCATION, 63

Fixed effects:
            Estimate Std. Error z value Pr(>|z|)
(Intercept)   0.2774     0.2107   1.316    0.188
YEAR96        1.2578     0.1821   6.906 4.97e-12 ***
YEAR97       -1.0856     0.2010  -5.400 6.67e-08 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Correlation of Fixed Effects:
       (Intr) YEAR96
YEAR96 -0.536
YEAR97 -0.439  0.552

AIC sekarang 1863.9, yang merupakan peningkatan lebih lanjut.

Variansi efek acak untuk LOKASI adalah 1.4679 dan untuk INDEX adalah 0.5081. Kita dapat melihat bahwa efek acak dari INDEX lebih kecil daripada efek acak dari LOCATION.

Model koefisien acak

Mari kita tambahkan efek acak $\eta_j$ oleh LOCATION tidak hanya pada intersep tetapi juga pada koefisien.

\log \lambda_i = (\beta_1 + \eta_{1j}) + (\beta_2 + \eta_{2j}), \quad \eta_{1j} \sim N(0, s^2), \quad \eta_{2j} \sim N(0, \sigma^2)

Model ini juga disebut model koefisien acak karena efek acak dimasukkan dalam koefisien.

Kode berikut dapat mengestimasi $\beta$ , $s$ , dan $\sigma$ . Untuk memasukkan efek acak dalam intersep dan koefisien, Anda dapat menulis TICKS ~ YEAR + (YEAR | LOCATION).

> fit_glmm <- glmer(TICKS ~ YEAR + (YEAR | LOCATION), family="poisson", data=grouseticks)
> summary(fit_glmm)

Generalized linear mixed model fit by maximum likelihood (Laplace Approximation) ['glmerMod']
 Family: poisson  ( log )
Formula: TICKS ~ YEAR + (YEAR | LOCATION)
   Data: grouseticks

     AIC      BIC   logLik deviance df.resid
  2266.7   2302.7  -1124.3   2248.7      394

Scaled residuals:
    Min      1Q  Median      3Q     Max
-6.6442 -0.8112 -0.4797  0.8437  5.5779

Random effects:
 Groups   Name        Variance Std.Dev. Corr
 LOCATION (Intercept) 2.3583   1.5357
          YEAR96      0.6002   0.7747   -0.70
          YEAR97      0.6735   0.8207   -0.80  0.46
Number of obs: 403, groups:  LOCATION, 63

Fixed effects:
            Estimate Std. Error z value Pr(>|z|)
(Intercept)   0.3273     0.2674   1.224  0.22083
YEAR96        1.3094     0.2542   5.152 2.58e-07 ***
YEAR97       -0.7578     0.2909  -2.605  0.00918 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Correlation of Fixed Effects:
       (Intr) YEAR96
YEAR96 -0.746
YEAR97 -0.668  0.553

Namun, estimasi ini adalah untuk model yang mengasumsikan korelasi antara $\eta_{1j}$ dan $\eta_{2j}$ . Jika Anda ingin menyesuaikan model dengan asumsi bahwa kedua parameter tidak bergantung satu sama lain, tuliskan TICKS ~ YEAR + (1 | LOCATION) + (0 + YEAR | LOCATION).

> fit_glmm <- glmer(TICKS ~ YEAR + (1 | LOCATION) + (0 + YEAR | LOCATION), family="poisson", data=grouseticks)
> summary(fit_glmm)

Generalized linear mixed model fit by maximum likelihood (Laplace Approximation) ['glmerMod']
 Family: poisson  ( log )
Formula: TICKS ~ YEAR + (1 | LOCATION) + (0 + YEAR | LOCATION)
   Data: grouseticks

     AIC      BIC   logLik deviance df.resid
  2268.7   2308.7  -1124.3   2248.7      393

Scaled residuals:
    Min      1Q  Median      3Q     Max
-6.6442 -0.8112 -0.4797  0.8437  5.5779

Random effects:
 Groups     Name        Variance Std.Dev. Corr
 LOCATION   (Intercept) 0.4151   0.6443
 LOCATION.1 YEAR95      1.9431   1.3939
            YEAR96      0.8755   0.9357   0.85
            YEAR97      0.6006   0.7750   0.87 0.54
Number of obs: 403, groups:  LOCATION, 63

Fixed effects:
            Estimate Std. Error z value Pr(>|z|)
(Intercept)   0.3274     0.2674   1.224  0.22081
YEAR96        1.3094     0.2542   5.152 2.58e-07 ***
YEAR97       -0.7578     0.2909  -2.605  0.00918 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Correlation of Fixed Effects:
       (Intr) YEAR96
YEAR96 -0.746
YEAR97 -0.668  0.553

Hal ini juga memungkinkan untuk menambahkan efek acak hanya untuk koefisien dengan menulis TICKS ~ YEAR + (0 + YEAR | LOCATION).

> fit_glmm <- glmer(TICKS ~ YEAR + (0 + YEAR | LOCATION), family="poisson", data=grouseticks)

Warning message:
In checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv,  :
  Model failed to converge with max|grad| = 0.0139508 (tol = 0.002, component 1)

> summary(fit_glmm)

Generalized linear mixed model fit by maximum likelihood (Laplace Approximation) ['glmerMod']
 Family: poisson  ( log )
Formula: TICKS ~ YEAR + (0 + YEAR | LOCATION)
   Data: grouseticks

     AIC      BIC   logLik deviance df.resid
  2266.7   2302.7  -1124.3   2248.7      394

Scaled residuals:
    Min      1Q  Median      3Q     Max
-6.6442 -0.8114 -0.4793  0.8432  5.5778

Random effects:
 Groups   Name   Variance Std.Dev. Corr
 LOCATION YEAR95 2.363    1.537
          YEAR96 1.291    1.136    0.87
          YEAR97 1.016    1.008    0.87 0.70
Number of obs: 403, groups:  LOCATION, 63

Fixed effects:
            Estimate Std. Error z value Pr(>|z|)
(Intercept)   0.3276     0.2676   1.224  0.22093
YEAR96        1.3099     0.2543   5.151 2.59e-07 ***
YEAR97       -0.7566     0.2908  -2.601  0.00929 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Correlation of Fixed Effects:
       (Intr) YEAR96
YEAR96 -0.746
YEAR97 -0.669  0.554
optimizer (Nelder_Mead) convergence code: 0 (OK)
Model failed to converge with max|grad| = 0.0139508 (tol = 0.002, component 1)

Kode R

Kode R untuk menggambarkan overdispersi distribusi Poisson ditunjukkan di bawah ini.

> set.seed(1)
> hist(Y1 <- rpois(1000, 1), breaks=seq(0, 20), col="#FF00007F", freq=F, ylim=c(0, 0.8), las=1,
     main="", xlab="X")
> hist(Y2 <- rpois(1000, 1 * exp(rnorm(1000, mean=0, sd=1))), col="#0000FF7F", add=T, freq=F, breaks=seq(0, 100))
> legend("right", legend=c("Poisson", "overdispersed Poisson"), pch=15, col=c("#FF00007F", "#0000FF7F"),
       bty="n", cex=1.5)