2022-12-09

Distribusi Dirichlet

Apa itu distribusi Dirichlet

Distribusi Dirichlet adalah distribusi yang probabilitas $x_i$ dari setiap peristiwa yang terjadi ketika $K$ peristiwa masing-masing terjadi $\alpha_{i}-1$ kali. Perhatikan bahwa $\alpha_{i}$ tidak harus berupa bilangan bulat.

Fungsi densitas probabilitas dari distribusi Dirichlet dinyatakan dengan persamaan berikut:

f(x_1, x_2,.., x_{K-1}) = \frac{\Gamma(\sum^K_{i=1} \alpha_i)}{\prod_{i=1}^K\Gamma(\alpha_i)}\prod_{i=1}^Kx_i^{\alpha_i-1}

\sum^n_{i=1} = 1, \quad x_i \in \{0, 1 \}

Dalam persamaan di atas, kasus $K=2$ sesuai dengan fungsi densitas probabilitas dari distribusi beta. Dengan kata lain, distribusi Dirichlet adalah perluasan multivariat dari distribusi beta.

Nilai yang diharapkan dan varians dari distribusi Dirichlet

Nilai yang diharapkan dan varians dari distribusi Dirichlet masing-masing adalah sebagai berikut.

E(X_i)=\frac{\alpha_i}{\sum^{K}_{i=1}\alpha_i} \quad (i=1,2,...,K-1)

V(X_i)=\frac{\alpha_i(\sum^{K}_{i=1} \alpha_i-\alpha_i)}{(\sum^{K}_{i=1}\alpha_i)^2 (\sum^{K}_{i=1}\alpha_i + 1)} \quad (i=1,2,...,K-1)

Periksa efek parameter

Mari kita memvisualisasikan distribusi Dirichlet 3 dimensi ( $K=3$ ) dalam Python.

import numpy as np
from scipy import special
from scipy.stats import dirichlet
import matplotlib
import matplotlib.pyplot as plt

plt.style.use('ggplot')

class Dirichlet():
    def __init__(self, param: list) -> None:
        self.param = np.array(param)

    def pdf(self, x: list) -> np.float:
        x_ar = np.array(x)
        cons = np.prod(special.gamma(self.param))/(special.gamma(np.sum(self.param)))
        p = (1./cons) * np.prod(x_ar**(self.param-1))
        return p

    def plt_3d(self, nrow: int, ncol: int, n: int, zlim=None)->None:
        xdata = np.linspace(0, 1, 200)
        ydata = np.linspace(0, 1, 200)
        X,Y = np.meshgrid(xdata, ydata)
        z = []
        X[X+Y>1] = 0
        Y[X+Y>1] = 0
        for _x, _y, _z in zip(X.flatten(), Y.flatten(), (1-X-Y).flatten()):
            z.append(self.pdf([_x, _y, _z]))

        Z = np.array(z).reshape(X.shape)
        fig = plt.figure(figsize=(10, 3))
        ax = plt.axes(projection='3d')
        ax.plot_surface(X, Y, Z, cmap='plasma')
        ax.set_zlim(zlim)
        ax.set_xlabel("$x_1$")
        ax.set_ylabel("$x_2$")
        ax.set_zlabel("PDF")
        ax.set_title("Dir($\\vec{\\alpha} = $" + "%s)" % self.param)
        plt.show()

Dirichlet([1.,1.,1.]).plt_3d(2, 2, 1, zlim=(0, 2.1))
Dirichlet([5.,5.,5.]).plt_3d(2, 2, 2)
Dirichlet([5.,1.,1.]).plt_3d(2, 2, 3)
Dirichlet([1.,5.,1.]).plt_3d(2, 2, 2)

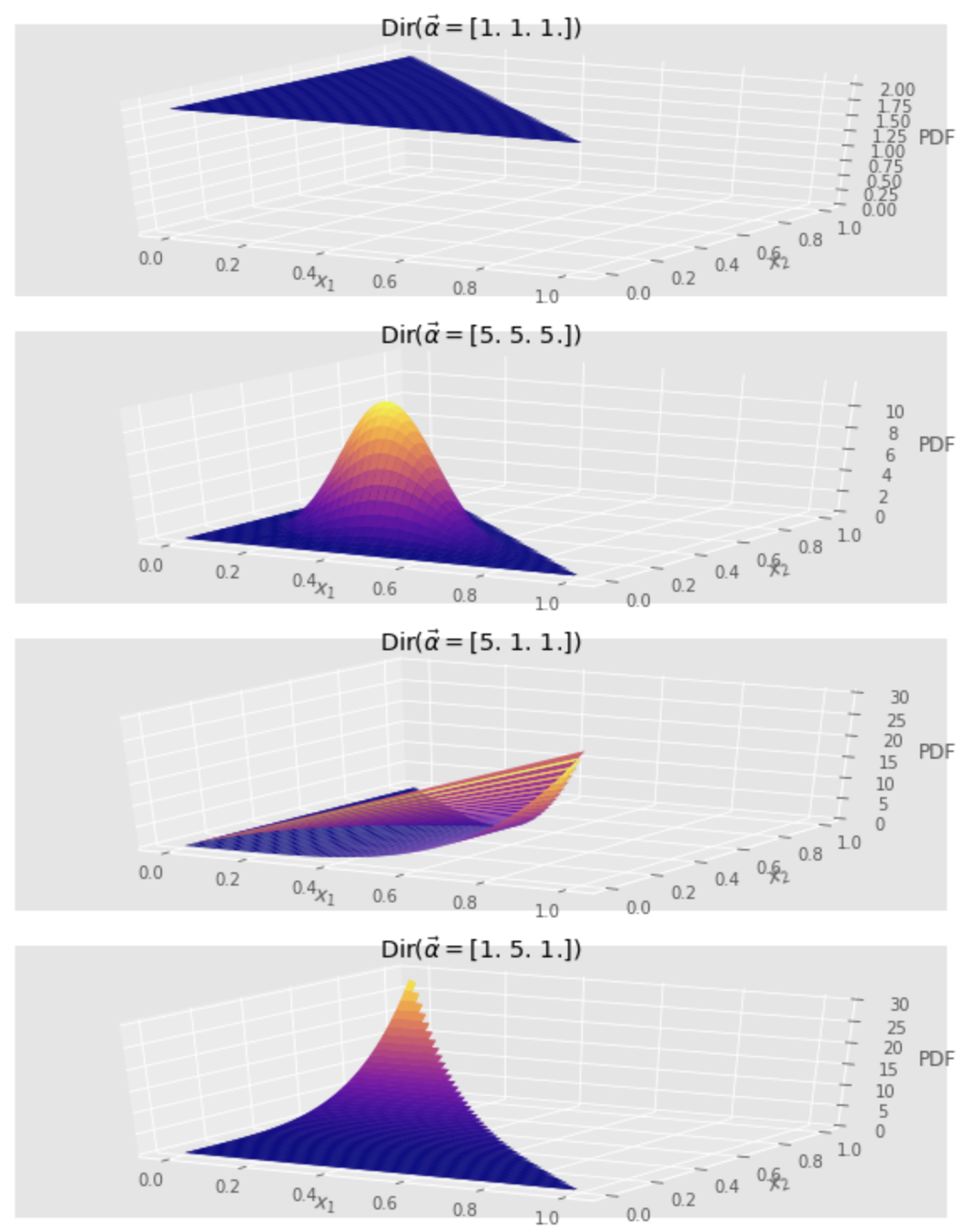
Dirichlet distribution

Ketika ketiga $\alpha$ memiliki nilai yang sama, kita dapat melihat bahwa semakin besar $\alpha$ , semakin kecil variansinya. Juga, kita dapat melihat bahwa variabel acak dengan $\alpha$ yang lebih besar memiliki kepadatan probabilitas yang lebih tinggi.

Distribusi Dirichlet

Apa itu distribusi Dirichlet

Nilai yang diharapkan dan varians dari distribusi Dirichlet

Periksa efek parameter

Distribusi eksponensial

Distribusi-t

Ryusei Kakujo