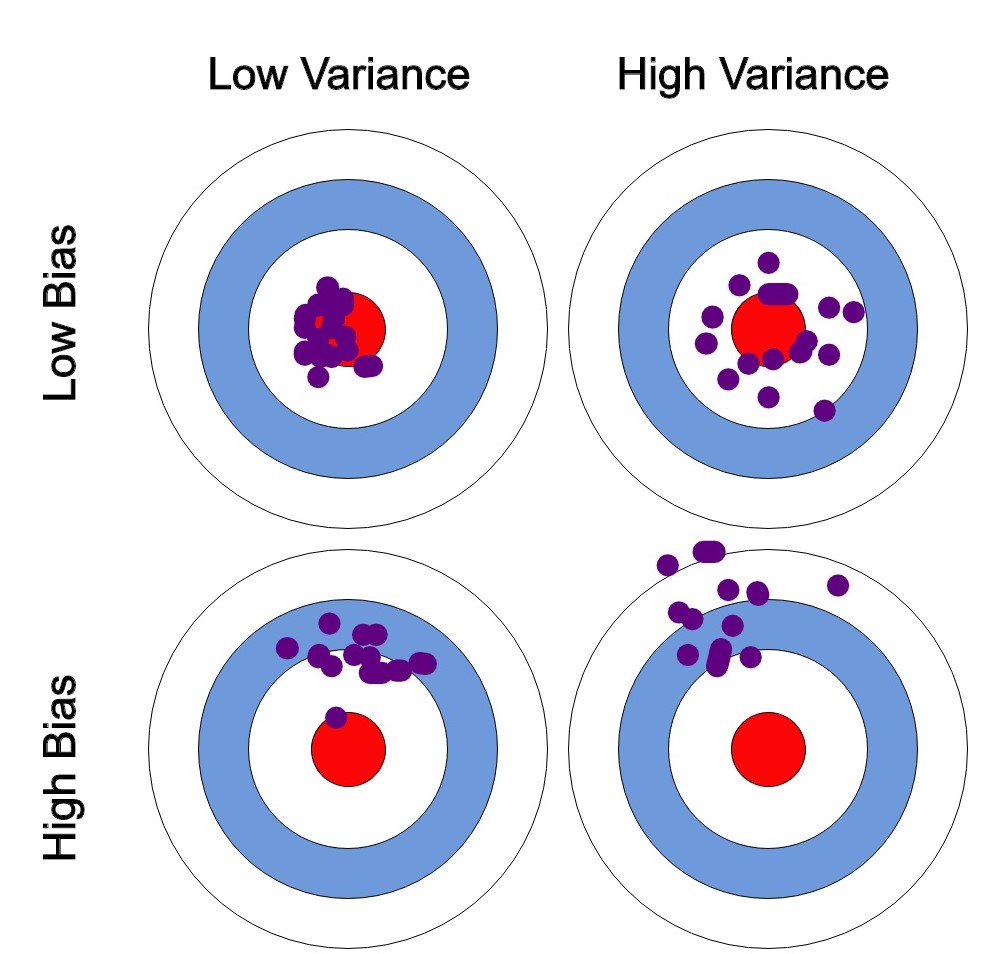
What is Bias-Variance Tradeoff
The bias-variance tradeoff is the process of finding the optimal balance between bias and variance to minimize the total prediction error. In general, increasing a model's complexity reduces its bias but increases its variance, while decreasing a model's complexity increases its bias but reduces its variance. The challenge is to find the right balance that leads to the best performance on new, unseen data.
Bias and Variance in Machine Learning
In this chapter, I will delve into the concepts of bias and variance, providing clear definitions and intuitive examples.
Bias: The Systematic Error
Bias refers to the error introduced by approximating a real-world problem with a simplified model. In the context of machine learning, bias measures how well the model's predictions align with the true values on average. A high-bias model makes strong assumptions about the data and can result in underfitting, where the model is too simple to capture the underlying patterns in the data.
For example, consider a dataset of housing prices with features such as square footage, number of bedrooms, and location. A high-bias model might assume that housing prices depend solely on square footage, ignoring the other features. This oversimplification could result in a poor fit to the data, as the model would not capture the variations in housing prices due to differences in the number of bedrooms or location.
Variance: The Random Error
Variance, on the other hand, is the error introduced by the model's sensitivity to small fluctuations in the training data. A high-variance model is highly flexible and can fit the training data very closely, but it is prone to overfitting, where the model becomes too specialized to the training data and performs poorly on new, unseen data.
Returning to the housing prices example, a high-variance model might fit the training data exceptionally well by taking into account all the available features and their complex interactions. However, this model may be overly sensitive to noise in the training data, such as outliers or measurement errors. As a result, it may not generalize well to new data, leading to poor performance on previously unseen housing prices.
Bias-Variance Decomposition
The bias-variance decomposition is a technique used to break down the total prediction error of a machine learning model into its bias and variance components, as well as the irreducible error. The total prediction error is given by:
The bias term represents the squared difference between the average prediction of the model and the true values. The variance term measures the model's sensitivity to small fluctuations in the data, while the irreducible error is inherent to the problem and cannot be reduced.
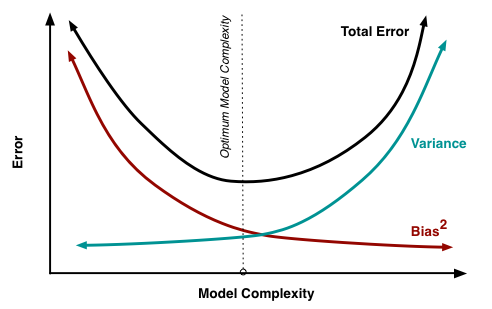
Understanding the Bias-Variance Tradeoff
Techniques for Managing the Tradeoff
In this chapter, I will introduce various techniques that can help you manage the bias-variance tradeoff effectively. By employing these strategies, data scientists can build models that strike the optimal balance between bias and variance, leading to better generalization and improved performance on new, unseen data.
Regularization
Regularization is a technique used to prevent overfitting by adding a penalty term to the model's objective function, effectively constraining its complexity. Two common types of regularization are L1 (Lasso) and L2 (Ridge) regularization.
By incorporating regularization, you can control the model's complexity and mitigate overfitting, resulting in a better balance between bias and variance.
Cross Validation
Cross validation is a technique for evaluating the performance of a machine learning model by dividing the dataset into multiple training and validation sets. The most common form of cross-validation is k-fold cross validation, where the dataset is divided into k equally sized folds. The model is trained on k-1 folds and validated on the remaining fold, with this process repeated k times, using a different fold for validation each time.
Cross-validation provides a more accurate assessment of a model's performance on unseen data, allowing you to compare different models or hyperparameter settings and select the one that achieves the best balance between bias and variance.
Ensemble Learning
Ensemble learning is a technique that combines the predictions of multiple base models to create a more accurate and robust overall prediction. There are several types of ensemble learning methods, including bagging, boosting, and stacking.
Ensemble learning techniques can help mitigate the effects of both high bias and high variance, improving the overall balance between the two and enhancing the model's performance on new data.
References