2022-12-28

ネステッドロジットモデル

Statistics

Statistical Model

Discrete Choice Model

ネステッドロジットモデルとは

ネステッドロジットモデルは、決定肢の間に観測されない類似性を考慮するために、標準の多項ロジットモデルを拡張した離散選択モデルです。多項ロジットモデルの主要な制限である、不要な代替物からの独立性仮定（IIA）が成立しない状況で使用できます。

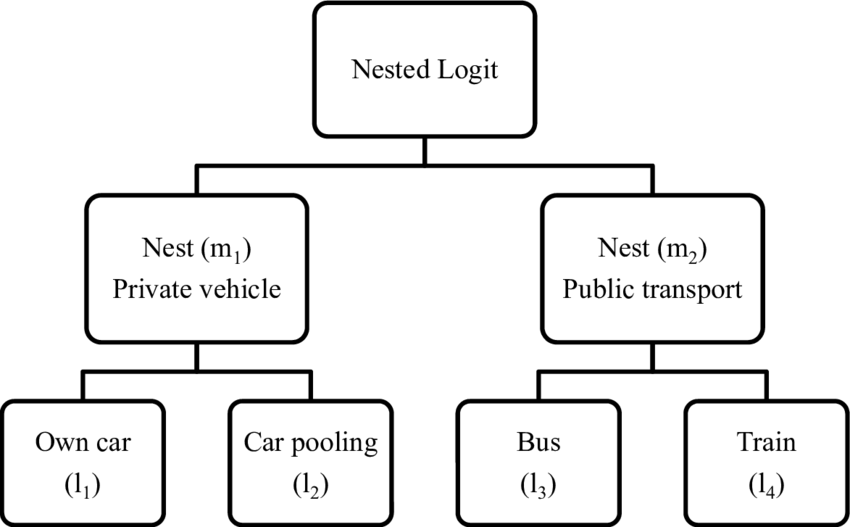
ネステッドロジットモデルでは、階層的なネスト構造に決定肢を配置し、各ネストにはいくつかの共通の特性を共有する代替物が含まれます。

Nested Logit Model
APPLICATION OF NEURAL NETWORK FOR MODE CHOICE MODELING AND MODAL TRAFFIC FORECASTING

ネステッドロジットモデルは、交通需要モデリング、市場シェア分析や製品選択、環境・資源経済学、保健経済学など、さまざまな分野で広く適用されています。ネステッドロジットモデルの高度なトピックと拡張には、クロスネストロジットモデル、ミックスロジットモデル、潜在クラスモデル、パネルデータまたは動的ネステッドロジットモデルが含まれます。これらの拡張は、複雑な意思決定問題に対処するために、ネステッドロジットフレームワークの柔軟性と適用範囲をさらに向上させます。

ネステッドロジットモデルの理論的基盤

ネステッドロジットモデルの導出

ネステッドロジットモデルを導出するために、まず決定肢を階層的なネスト構造にグループ化します。各ネストには、観測されない共通の特性を共有する代替物が含まれます。選択プロセスは2段階で行われます。最初に、個人はネストを選択し、次にそのネスト内の代替物を選択します。

$G$ をネストの集合とし、 $J_g$ をネスト $g$ 内の代替物の集合とします。個人 $i$ がネスト $g$ 内の代替物 $j$ を選択する確率は次のように表現されます。

P_{ij} = P_i(j|g) \cdot P_i(g)

ここで、 $P_i(j|g)$ は、ネスト $g$ が与えられた場合に代替物 $j$ を選択する条件付き確率であり、 $P_i(g)$ はネスト $g$ を選択する確率です。

ランダム効用最大化理論を採用し、効用のランダム成分がガンベル分布に従うと仮定することで、ネステッドロジットモデルを導出できます。

P_{ij} = \frac{\exp\left(\frac{V_{ij}}{\tau_g}\right)}{\sum_{j' \in J_g} \exp\left(\frac{V_{i(j')}}{\tau_g}\right)} \cdot \frac{\left(\sum_{j \in J_g} \exp\left(\frac{V_{ij}}{\tau_g}\right)\right)^{(1 - \tau_g)}}{\sum_{g' \in G} \sum_{j' \in J_{(g')}} \exp\left(\frac{V_{i(j')}}{\tau_{(g')}}\right)^{(1 - \tau_{(g')})}}

ここで、 $\tau_g$ はネスト $g$ の相違パラメータであり、同じネスト内の代替物間の相関度を測定します。 $\sum_{j \in J_g} \exp\left(\frac{V_{ij}}{\tau_g}\right)$ は、ネスト $g$ の包括的価値と呼ばれます。

包含価値（IV）と相違パラメータ

ネスト $g$ の包含価値（Inclusive Value, IV）は、そのネスト内での期待最大効用を表します。特定のネストを選択する確率を計算する上で、包含価値は重要な役割を果たします。包括的価値が高いほど、特定のネストを選択する確率が高くなります。

相違パラメータ $\tau_g$ は、ネスト内の代替物間の相関度を測定します。 $\tau_g$ が1に等しい場合、ネステッドロジットモデルは多項ロジットモデルに簡約され、IIA仮定が成立します。 $\tau_g$ が0に近づくにつれ、ネスト内の代替物はより似ており、それらの相関関係が増加します。モデルが効用最大化と一致するために、相違パラメータは0から1の範囲内にある必要があります。

ネステッドロジットモデルとR

この章では、Rを使用してネステッドロジットモデルを推定する方法の例を示します。ネステッドロジットモデルを含むさまざまな離散選択モデルを推定することができるmlogitパッケージを使用します。例として、AERパッケージからTravelModeデータセットを使用します。

TravelModeデータセットには、交通手段を選択する際に個人が行った選択に関する情報が含まれています。データセットには次の変数があります。

id: 個人の識別子
mode: 交通手段（飛行機、電車、自動車、バス）
choice: 選択された交通手段を示す2値変数（選択された場合は1、そうでない場合は0）
gcost: 交通手段の総費用
wait: 交通手段の待ち時間

データの準備

パッケージをインストールし、TravelModeデータセットを読み込みます。

# Install mlogit and AER packages and load them. Latter is just for a dataset we'll be using.
# install.packages("mlogit", "AER")
library("mlogit", "AER")

# Load dataset TravelMode
data("TravelMode", package = "AER")

テーブルを表示します。

show(TravelMode)

    individual  mode choice wait vcost travel gcost income size
1            1   air     no   69    59    100    70     35    1
2            1 train     no   34    31    372    71     35    1
3            1   bus     no   35    25    417    70     35    1
4            1   car    yes    0    10    180    30     35    1
5            2   air     no   64    58     68    68     30    2
6            2 train     no   44    31    354    84     30    2
7            2   bus     no   53    25    399    85     30    2
8            2   car    yes    0    11    255    50     30    2
9            3   air     no   69   115    125   129     40    1
10           3 train     no   34    98    892   195     40    1
11           3   bus     no   35    53    882   149     40    1
12           3   car    yes    0    23    720   101     40    1

モデルの推定

ネステッドロジットモデルを推定します。

# Use the mlogit() function to run a nested logit estimation

# Here, we will predict what mode of travel individuals
# choose using cost and wait times

nested_logit_model = mlogit(
  choice ~ gcost + wait,
  data = TravelMode,
  ##The variable from which our nests are determined
  alt.var = 'mode',
  #The variable that dictates the binary choice
  choice = 'choice',
  #List of nests as named vectors
  nests = list(fast = c('air','train'), slow = c('car','bus'))
  )

alt.var = 'mode'
この引数は、異なる代替手段（この場合は交通手段）を含むデータセット内の変数の名前を指定します。ここでは、代替手段は'mode'変数に格納されています。
choice = 'choice'
この引数は、代替手段が選択されたかどうかを示すデータセット内の変数の名前を指定します（1：選択された、0：選択されていない）。この場合、バイナリー選択変数は'choice'と呼ばれます。
nests = list(fast = c('air','train'), slow = c('car','bus'))
この引数は、ネステッドロジットモデルのネストを定義します。ネストは、名前付きベクトルのリストとして指定され、各ベクトルには特定のネストに属する代替手段が含まれています。この場合、2つのネストがあります。 'fast'（'air'と'train'を含む）と'slow'（'car'と'bus'を含む）です。

nested_logit_modelオブジェクトを使用して、summary()関数を呼び出すことで、様々なモデル統計を取得することができます。

# The results
summary(nested_logit_model)

Call:
mlogit(formula = choice ~ gcost + wait, data = TravelMode, nests = list(fast = c("air",
    "train"), slow = c("car", "bus")), alt.var = "mode", choice = "choice")

Frequencies of alternatives:choice
    air   train     bus     car
0.27619 0.30000 0.14286 0.28095

bfgs method
15 iterations, 0h:0m:0s
g'(-H)^-1g = 2.04E-07
gradient close to zero

Coefficients :
                    Estimate Std. Error z-value  Pr(>|z|)
(Intercept):train -2.6632486  0.8797054 -3.0274  0.002466 **
(Intercept):bus   -2.9341306  0.9247620 -3.1728  0.001510 **
(Intercept):car   -8.0988987  1.8709536 -4.3288 1.500e-05 ***
gcost             -0.0234085  0.0059397 -3.9410 8.115e-05 ***
wait              -0.1499260  0.0364437 -4.1139 3.890e-05 ***
iv:fast            2.3918823  0.9701086  2.4656  0.013679 *
iv:slow            0.9745729  0.3598853  2.7080  0.006769 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Log-Likelihood: -189.74
McFadden R^2:  0.33132
Likelihood ratio test : chisq = 188.03 (p.value = < 2.22e-16)

以下は、ネステッドロジットモデルの結果の解釈です。

Frequencies of alternatives
頻度は、データセットで選択された各交通手段の割合を示しています。この場合、27.62％の人が空路、30.00％が鉄道、14.29％がバス、28.10％が車を選択しました。これらの値は、各モードの人気度のベースラインを提供します。
Coefficients
係数は、予測変数と特定の交通手段を選択する対数オッズの関係を表します（この場合、航空モードを基準カテゴリーとします）。正の係数は、モードの選択の対数オッズの増加を示し、負の係数は、減少を示します。
(Intercept):train, (Intercept):bus, (Intercept):car
これらは、列車、バス、および車のそれぞれの代替手段に対する特定の代替手段定数です。これらは、全ての予測変数がゼロである場合に、航空モードを選択する対数オッズのベースラインを表します。3つの代替手段全ての負の係数は、予測変数の値が等しい場合、それぞれのモードを選択する対数オッズが航空を選択する対数オッズより低いことを示しています。
gcost
一般化費用には負の係数（-0.0234）があり、交通手段の一般化費用が増加するにつれて、その交通手段を選択する可能性が減少することを示しています。この結果は、低いp値（8.115e-05）で示されるように、統計的に有意です。
wait
待ち時間には、負の係数（-0.1499）があり、交通手段の待ち時間が増加するにつれて、その交通手段を選択する可能性が減少することを意味します。この結果も、p値が3.890e-05で統計的に有意です。
包含価値(iv) parameters
包含価値（IV）パラメータは、各ネスト内の代替品の類似性を表します。fast（iv：fast = 2.3919、p値= 0.0137）とslow（iv：slow = 0.9746、p値= 0.0068）ネストの両方に対する正のかつ統計的に有意な係数は、これらのネスト内の代替手段の選択に影響を与える観測されていない要因が正の相関関係にあることを示しています。
Log-Likelihood
対数尤度値-189.74は、モデルがデータに適合している程度の尺度です。より高い値はより良い適合を示します。
McFadden R^2
McFadden R^2値0.3313は、モデルの適合度を示す尺度です。 0から1の範囲で、高い値はより良い適合を示します。この値は、モデルがデータの33.13％の変動を説明していることを示唆しています。
Likelihood ratio test
尤度比検定統計量（カイ二乗= 188.03）およびp値（<2.22e-16）は、このモデルが統計的に有意であり、予測変数のないモデルよりも改善されたことを示しています。

ネステッドロジットモデルの結果は、一般的なコストと待ち時間が交通手段の選択に負の影響を与え、低コストで待ち時間が短い代替手段を好むことを示しています。また、正のかつ有意な包含価値（IV）パラメータは、各ネスト内の代替手段の選択に影響を与える観測されていない要因が相関関係にあることを示唆しています。