2022-08-04

決定木におけるFeature Importance

Machine Learning

Decision Tree

sklearn

Python

はじめに

決定木は、機械学習アルゴリズムの中でも、その単純さ、解釈性、視覚化の容易さから人気があります。決定木の重要な側面の1つは、データセット内のもっとも関連性の高い特徴量を自動的に選択およびランク付けする能力です。このプロセスは、Feature Importanceと呼ばれ、複雑なデータセットを簡素化し、もっとも重要な変数を特定するのに役立ちます。この記事では、決定木におけるFeature Importanceの概念について詳しく掘り下げ、ジニ不純度、Information Gain、ゲイン比など、その計算に使用されるさまざまな方法について説明します。

ジニ不純度

ジニ不純度とは、データセットからランダムに選択した要素が、その部分集合内のラベルの分布に従ってランダムにラベル付けされた場合に、誤ってラベル付けされる頻度を測定する指標です。ジニ不純度は、各特徴量に対して計算され、決定木アルゴリズムは、各ノードでデータセットを分割するために、ジニ不純度がもっとも低い特徴量を選択します。特徴量の総合的な重要性は、木全体を通じてもたらされるジニ不純度の累積的な減少によって決定されます。

数式的には、データセット $S$ のジニ不純度は次のように計算されます。

Gini(S) = 1 - \sum (p_i)^2

ここで、 $p_i$ は要素がクラス $i$ に属する確率です。

ジニ不純度は、決定木の各ノードで分割する特徴量を決定するために使用されます。分割後の加重平均ジニ不純度がもっとも低い特徴量が選択されます。

Information Gain

Information Gainは、決定木でFeature Importanceを計算するために使用される別の手法です。このアプローチは、データセットのランダム性や無秩序さを測定するエントロピーの概念に基づいています。Information Gainは、特定の特徴量に基づいてデータセットを分割した結果、エントロピーがどれだけ減少したかを計算します。もっとも高いInformation Gainを示す特徴量が各ノードでのデータセットの分割に選択されます。特徴量の全体的な重要性は、木全体で提供されるInformation Gainの累積によって決定されます。

データセット $S$ のエントロピーは次のように計算できます。

Entropy(S) = - \sum p_i * \log_2(p_i)

ここで、 $p_i$ は要素がクラス $i$ に属する確率です。

Information Gainは、次の式で計算されます。

InformationGain(S, A) = Entropy(S) - \sum ((|S_v| / |S|) * Entropy(S_v))

ここで、 $A$ は考慮される特徴量、 $S_v$ は特徴量 $A$ の値 $v$ を持つデータセットの部分集合を表し、 $|S_v|$ と $|S|$ はそれぞれ部分集合 $S_v$ と $S$ のサイズを表します。

ゲイン比

ゲイン比は、特徴量の固有情報を考慮するInformation Gainの変種です。Information Gainにおける大きな数の異なる値を持つ特徴量に対するバイアスに対処します。ゲイン比は、Information Gainを特徴量の固有情報で除算することによって計算されます。各ノードで分割するために、ゲイン比がもっとも高い特徴量が選択され、特徴量の総合的な重要性は、木全体を通じてもたらされるゲイン比の累積によって決定されます。

特徴量 $A$ の固有情報は次のように計算できます。

IntrinsicInformation(A) = - \sum ((|S_v| / |S|) * \log_2(|S_v| / |S|))

ここで、 $S_v$ は特徴量 $A$ の値 $v$ を持つデータセットの部分集合を表し、 $|S_v|$ と $|S|$ はそれぞれ部分集合 $S_v$ と $S$ のサイズを表します。

ゲイン比は、次の式で計算されます。

GainRatio(S, A) = InformationGain(S, A) / IntrinsicInformation(A)

Feature Importanceの可視化

このセクションでは、Pythonを使用して回帰および分類ケースでのFeature Importanceを可視化する方法を示します。

まず、必要なライブラリをインポートし、データセットを作成します。

python

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression, make_classification
from sklearn.tree import DecisionTreeRegressor, DecisionTreeClassifier
from sklearn.model_selection import train_test_split

# Create synthetic datasets for regression and classification
X_reg, y_reg = make_regression(n_samples=1000, n_features=10, n_informative=5, random_state=42)
X_clf, y_clf = make_classification(n_samples=1000, n_features=10, n_informative=5, random_state=42)

# Split the datasets into train and test sets
X_reg_train, X_reg_test, y_reg_train, y_reg_test = train_test_split(X_reg, y_reg, test_size=0.3, random_state=42)
X_clf_train, X_clf_test, y_clf_train, y_clf_test = train_test_split(X_clf, y_clf, test_size=0.3, random_state=42)

次に、回帰および分類の決定木モデルを作成およびトレーニングします。

python

# Create and train decision tree models
regressor = DecisionTreeRegressor(random_state=42)
classifier = DecisionTreeClassifier(random_state=42)

regressor.fit(X_reg_train, y_reg_train)
classifier.fit(X_clf_train, y_clf_train)

モデルがトレーニングされたら、Feature Importance値を取得し、それらを可視化します。

python

# Get feature importance values for regression and classification models
reg_importance = regressor.feature_importances_
clf_importance = classifier.feature_importances_

# Function to visualize feature importance
def plot_feature_importance(importances, title):
    indices = np.argsort(importances)[::-1]
    plt.figure()
    plt.title(title)
    plt.bar(range(len(importances)), importances[indices], align='center')
    plt.xticks(range(len(importances)), indices)
    plt.xlabel('Feature Index')
    plt.ylabel('Feature Importance')
    plt.show()

# Visualize feature importance for regression and classification
plot_feature_importance(reg_importance, 'Feature Importance for Regression')
plot_feature_importance(clf_importance, 'Feature Importance for Classification')

Feature importance for regression
Feature importance for classification

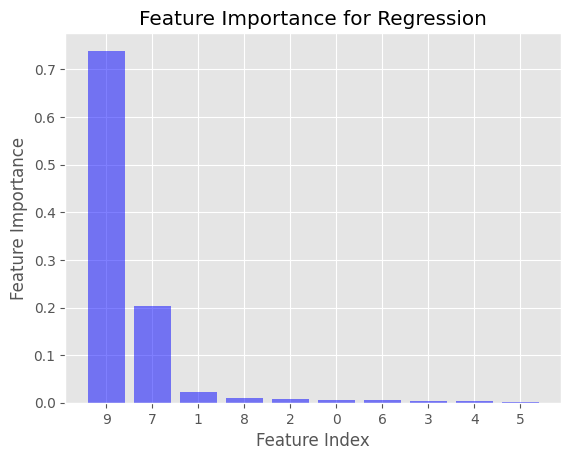
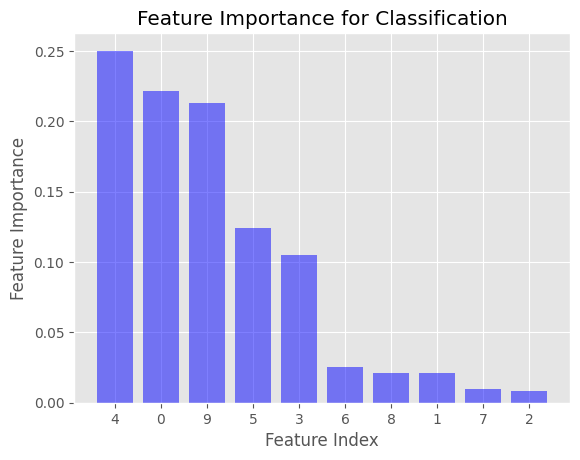
これにより、回帰および分類ケースでのFeature Importance値を表示する2つの棒グラフが生成されます。x軸は特徴量のインデックスを、y軸はFeature Importance値を表します。特徴量は重要性の降順で並べ替えられます。

例では、DecisionTreeClassifierではジニ不純度、DecisionTreeRegressorでは平均二乗誤差（MSE）を使用してFeature Importanceが計算されています。これらは、Scikit-learnライブラリで決定木を作成する際にデフォルトで使用される不純度基準です。

DecisionTreeRegressorおよびDecisionTreeClassifierの不純度基準を変更することができます。DecisionTreeClassifierの場合、criterionパラメータを'entropy'に設定することでジニ不純度の代わりにInformation Gainを使用できます。DecisionTreeRegressorの場合、別の不純度の測定値を使用する場合は、criterionパラメータを'mae'（平均絶対誤差）に設定できます。ただし、Scikit-learnは、不純度基準としてのGain Ratioを直接サポートしていません。