2022-11-23

Regresi Polinomial

Machine Learning

Regression

Python

sklearn

Apa itu Regresi Polinomial

Regresi Polinomial adalah bentuk analisis regresi di mana hubungan antara variabel independen dan variabel dependen dimodelkan sebagai fungsi polinomial derajat ke-n. Dalam istilah yang lebih sederhana, Regresi Polinomial adalah perluasan dari Regresi Linier yang memungkinkan kita untuk menangkap hubungan nonlinier yang kompleks antara variabel. Regresi Polinomial menyediakan pendekatan yang fleksibel dan kuat untuk memodelkan data dengan tren melengkung, osilasi, atau pola kompleks lainnya.

Mengapa Menggunakan Regresi Polinomial

Meskipun model regresi linier mudah diinterpretasikan dan diimplementasikan, namun model tersebut memiliki keterbatasan dalam kemampuannya untuk menangkap hubungan yang kompleks antara variabel. Dalam banyak aplikasi dunia nyata, hubungan antara variabel input dan output tidak linear, dan garis lurus mungkin bukan representasi terbaik dari pola-pola yang mendasar pada data.

Regresi Polinomial memungkinkan kita untuk menyesuaikan kurva pada data, sehingga memungkinkan kita untuk memodelkan rentang hubungan yang lebih luas antara variabel. Beberapa keuntungan utama dari menggunakan Regresi Polinomial meliputi:

Fleksibilitas
Dengan menyesuaikan derajat polinomial, kita dapat mengontrol kompleksitas model, memungkinkan kita untuk menangkap berbagai pola pada data.
Interpretabilitas
Model Regresi Polinomial, meskipun lebih kompleks daripada model linier, masih relatif mudah diinterpretasikan dan dipahami.
Aplikabilitas
Regresi Polinomial dapat diterapkan pada berbagai masalah, mulai dari memprediksi harga perumahan hingga memodelkan penyebaran penyakit menular.

Matematika di Balik Regresi Polinomial

Regresi Linier: Dasar

Regresi linier adalah bentuk sederhana dari analisis regresi, di mana hubungan antara variabel independen $x$ dan variabel dependen $y$ dimodelkan sebagai fungsi linier. Persamaan untuk model regresi linier dapat direpresentasikan sebagai:

$y = \beta_0 + \beta_1x + \epsilon$

di mana $y$ adalah variabel dependen, $x$ adalah variabel independen, $\beta_0$ adalah intercept, $\beta_1$ adalah kemiringan garis, dan $\epsilon$ adalah istilah kesalahan.

Fungsi Polinomial

Fungsi polinomial adalah ekspresi matematis yang terdiri dari variabel dan koefisien, melibatkan hanya operasi penjumlahan, pengurangan, perkalian, dan eksponen bilangan bulat non-negatif. Polinomial derajat $n$ dapat direpresentasikan sebagai:

$P(x) = a_0 + a_1x + a_2x^2 + \cdots + a_nx^n$

di mana $a_i$ adalah koefisien dan $x$ adalah variabel.

Model Regresi Polinomial

Dalam Regresi Polinomial, kita memperluas model regresi linier dengan menyesuaikan fungsi polinomial pada data. Untuk regresi polinomial univariat derajat $n$ , persamaannya dapat direpresentasikan sebagai:

$y = \beta_0 + \beta_1x + \beta_2x^2 + \cdots + \beta_nx^n + \epsilon$

Tujuan dari Regresi Polinomial adalah menemukan koefisien $\beta_i$ yang terbaik pada data, dengan meminimalkan istilah kesalahan $\epsilon$ .

Menemukan Koefisien: Metode Kuadrat Terkecil

Metode Kuadrat Terkecil adalah teknik optimasi yang digunakan untuk menemukan koefisien yang paling cocok untuk model regresi polinomial. Tujuannya adalah untuk meminimalkan jumlah residual kuadrat (perbedaan antara nilai observasi dan nilai prediksi), yang dikenal sebagai residual sum of squares (RSS).

$RSS(\beta) = \sum_{i=1}^{N} [y_i - (\beta_0 + \beta_1x_i + \beta_2x_i^2 + \cdots + \beta_nx_i^n)]^2$

Untuk menemukan koefisien yang meminimalkan RSS, kita dapat mengambil turunan parsial dari fungsi RSS terhadap setiap koefisien dan mengatur hasilnya sama dengan nol. Menyelesaikan sistem persamaan linear ini akan memberikan nilai optimal untuk koefisien $\beta_i$ .

Implementasi Regresi Polinomial pada Python

Di bab ini, saya akan menunjukkan bagaimana cara mengimplementasikan regresi polinomial menggunakan Python, dengan fokus pada dataset "mpg" yang populer.

Pertama, kita akan mengimpor pustaka yang diperlukan dan memuat dataset "mpg". Dataset tersedia di pustaka seaborn.

python

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score

# Load the mpg dataset
mpg = sns.load_dataset("mpg")

# Display the first five rows
print(mpg.head())

    mpg  cylinders  displacement  horsepower  weight  acceleration  \
0  18.0          8         307.0       130.0    3504          12.0
1  15.0          8         350.0       165.0    3693          11.5
2  18.0          8         318.0       150.0    3436          11.0
3  16.0          8         304.0       150.0    3433          12.0
4  17.0          8         302.0       140.0    3449          10.5

   model_year origin                       name
0          70    usa  chevrolet chevelle malibu
1          70    usa          buick skylark 320
2          70    usa         plymouth satellite
3          70    usa              amc rebel sst
4          70    usa                ford torino

Pada contoh ini, kita akan menggunakan fitur horsepower sebagai variabel independen (x) dan mpg sebagai variabel dependen (y). Kita juga akan menghapus baris apa pun yang memiliki nilai yang hilang.

python

# Remove missing values and select the relevant columns
mpg_cleaned = mpg[['horsepower', 'mpg']].dropna()

# Separate the features and the target variable
X = mpg_cleaned['horsepower'].values.reshape(-1, 1)
y = mpg_cleaned['mpg'].values

Sekarang kita akan membuat fitur polinomial untuk variabel independen horsepower. Pada contoh ini, kita akan menggunakan polinomial derajat 2.

python

# Create polynomial features
poly_features = PolynomialFeatures(degree=2)
X_poly = poly_features.fit_transform(X)

Kita akan membagi data menjadi set pelatihan dan pengujian, melatih model regresi polinomial kita, dan mengevaluasi kinerjanya menggunakan mean squared error (MSE) dan R-squared.

python

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X_poly, y, test_size=0.2, random_state=42)

# Train the polynomial regression model
poly_reg = LinearRegression()
poly_reg.fit(X_train, y_train)

# Make predictions and evaluate the model
y_pred = poly_reg.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

print("Mean Squared Error: ", round(mse, 2))
print("R-squared: ", round(r2, 2))

Mean Squared Error:  18.42
R-squared:  0.64

Akhirnya, kita akan memvisualisasikan regresi polinomial menggunakan matplotlib dan seaborn.

python

# Set seaborn style
sns.set(style="whitegrid")

# Create a scatterplot of the data
plt.figure(figsize=(10, 6))
plt.scatter(X, y, color='blue', alpha=0.5, label="Data points")

# Plot the polynomial regression curve
X_plot = np.linspace(X.min(), X.max(), 100).reshape(-1, 1)
X_plot_poly = poly_features.transform(X_plot)
y_plot = poly_reg.predict(X_plot_poly)
plt.plot(X_plot, y_plot, color='red', linewidth=2, label="Polynomial Regression")

# Customize the plot appearance
plt.xlabel("Horsepower")
plt.ylabel("Miles per Gallon (mpg)")
plt.title("Polynomial Regression of Degree 2: Horsepower vs. MPG")
plt.legend()
plt.show()

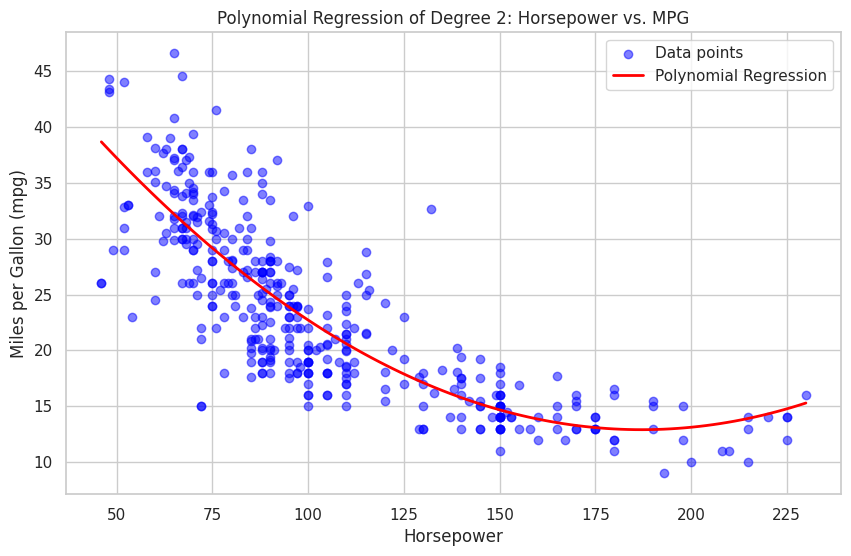
Polynomial regression

Plot hasilnya menampilkan regresi polinomial, menyoroti hubungan antara horsepower dan mpg. Anda dapat mencoba berbagai derajat polinomial atau fitur lain pada dataset untuk mengeksplorasi bagaimana kinerja model dan visualisasi berubah.