2022-11-24

Support Vector Regression (SVR)

Machine Learning

Regression

Python

sklearn

Apa itu Support Vector Regression (SVR)

Support Vector Regression (SVR) adalah algoritma pembelajaran mesin yang kuat dan serbaguna yang berasal dari Support Vector Machines (SVM) yang terkenal untuk klasifikasi. Tujuan utama dari SVR adalah untuk memprediksi variabel target kontinu, dengan diberikan sekumpulan fitur input.

Konsep Kunci dalam SVR

SVR bertujuan untuk mencari fungsi yang mendekati hubungan antara fitur input dan variabel target, dengan tujuan meminimalkan kesalahan prediksi dalam toleransi margin yang telah ditentukan. Konsep utama dalam SVR meliputi:

Support vector
Ini adalah titik data yang terletak pada atau di luar margin yang telah ditentukan sekitar fungsi pendekatan. Support vector memainkan peran penting dalam menentukan model SVR, karena mereka menentukan parameter yang optimal.

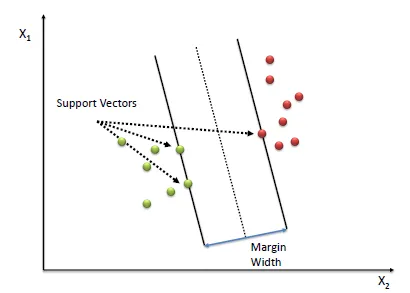
Machine Learning: Support Vector Regression (SVR)

Hyperplane
Hyperplane adalah subruang datar satu dimensi yang lebih rendah dari ruang ambien. Dalam konteks SVR, hyperplane digunakan untuk mendekati hubungan antara fitur input dan variabel target. Untuk SVR linear, hyperplane mewakili fungsi linier, sedangkan untuk SVR non-linier, hyperplane ada di ruang dimensi yang lebih tinggi yang diperoleh melalui transformasi kernel.

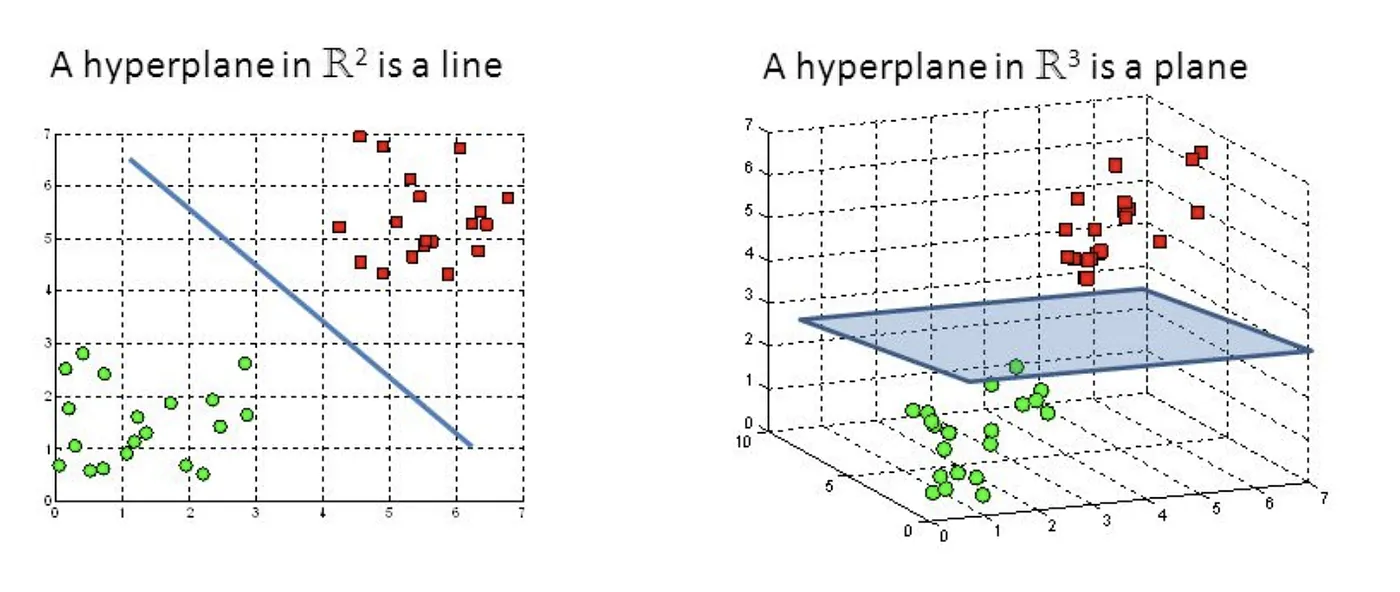
Hyperplane
Machine Learning: Support Vector Regression (SVR)

Margin
Margin adalah zona toleransi sekitar fungsi pendekatan (hyperplane) di mana kesalahan dianggap dapat diterima. SVR bertujuan untuk memaksimalkan margin sambil menjaga kesalahan prediksi dalam toleransi yang ditentukan. Lebar margin ditentukan oleh parameter $\epsilon$ .

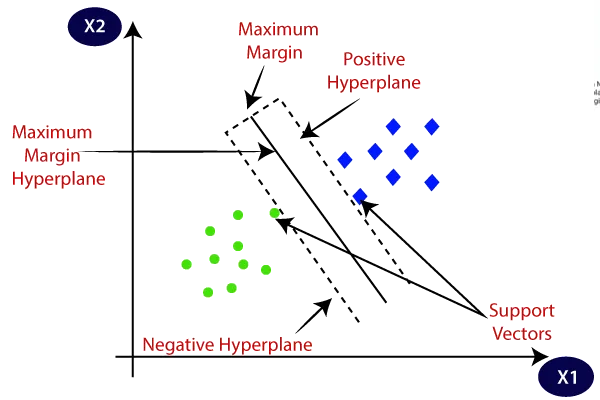
Margin
Machine Learning: Support Vector Regression (SVR)

SVR
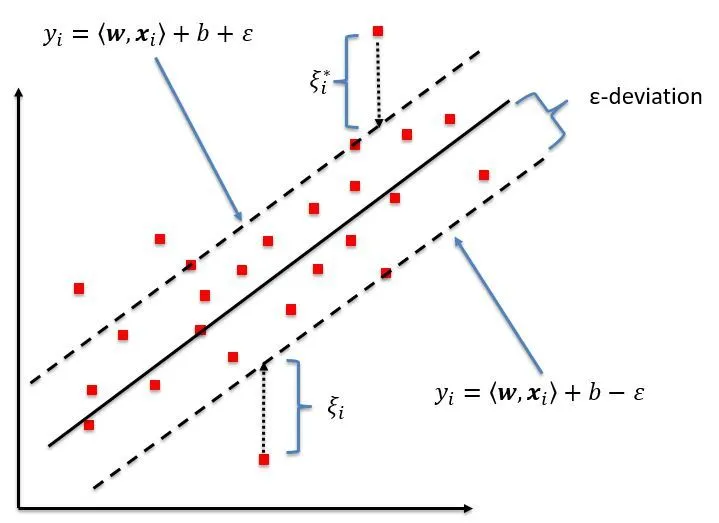
Machine Learning: Support Vector Regression (SVR)

Kernel Trick
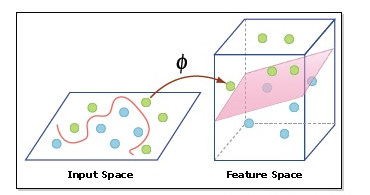
Kernel trick adalah teknik yang digunakan dalam SVR non-linier untuk menemukan fungsi non-linier yang paling baik mendekati hubungan antara fitur input dan variabel target, sambil menjaga kesalahan prediksi dalam toleransi margin yang ditentukan. Kernel trick melibatkan pemetaan data input ke ruang dimensi yang lebih tinggi dengan menggunakan fungsi kernel, di mana fungsi linier dapat digunakan untuk mendekati hubungan non-linier. Hal ini memungkinkan SVR untuk menyelesaikan masalah non-linier tanpa secara eksplisit mentransformasikan data input, sehingga mengurangi kompleksitas komputasi.

kernel
Support Vector Regression Tutorial for Machine Learning

Dasar Matematika SVR

Regresi Linear vs. SVR

Dalam regresi linear, kita mencoba menemukan garis penyesuaian terbaik dengan meminimalkan kesalahan kuadrat antara nilai prediksi dan nilai aktual. Fungsi linear diberikan oleh:

f(x) = w^T x + b

Di sisi lain, SVR berfokus pada mencari fungsi yang berada dalam margin (toleransi) yang telah ditentukan sekitar nilai target yang sebenarnya.

Masalah Optimasi

SVR bertujuan untuk menemukan vektor bobot optimal $w$ dan istilah bias $b$ dengan menyelesaikan masalah optimasi berikut:

Fungsi Objektif

\min_{w, b} \frac{1}{2} ||w||^2 + C \sum_{i=1}^N (\xi_i + \xi_i^*)

Dimana $||w||^2$ adalah norm kuadrat dari vektor bobot $w$ , $C$ adalah parameter regularisasi, $N$ adalah jumlah titik data, dan $\xi_i$ dan $\xi_i^*$ adalah variabel slack yang mengukur penyimpangan prediksi dari nilai target yang sebenarnya.

Kendala

Kendala untuk masalah optimasi didefinisikan sebagai berikut:

\begin{aligned} y_i - f(x_i) &\leq \epsilon + \xi_i \\ f(x_i) - y_i &\leq \epsilon + \xi_i^* \\ \xi_i, \xi_i^* &\geq 0, \quad i = 1, \dots, N \end{aligned}

Dimana $y_i$ adalah nilai target yang sebenarnya untuk titik data ke- $i$ , dan $\epsilon$ adalah margin toleransi.

Fungsi Kerugian

SVR menggunakan fungsi kerugian epsilon-insensitive, yang didefinisikan sebagai berikut:

L_\epsilon(y, f(x)) = \max(0, |y - f(x)| - \epsilon)

Fungsi kerugian epsilon-insensitive tidak menghukum kesalahan yang berada dalam margin toleransi $\epsilon$ yang ditentukan sebelumnya.

Formulasi Dual

Formulasi dual dari masalah SVR diperoleh dengan menerapkan kondisi Karush-Kuhn-Tucker (KKT) pada fungsi Lagrange. Reformulasi ini memungkinkan kita untuk menyelesaikan masalah optimasi lebih efisien dan untuk menggabungkan kernel non-linear.

Pengganda Lagrange

Untuk mendapatkan masalah dual, kita memperkenalkan pengganda Lagrange $\alpha_i,\alpha_i^*\geq 0$ untuk setiap kendala dalam masalah optimasi. Fungsi Lagrange kemudian didefinisikan sebagai berikut:

\mathcal{L}(w, b, \xi, \xi^*, \alpha, \alpha^*) = \frac{1}{2} ||w||^2 + C \sum_{i=1}^N (\xi_i + \xi_i^*) - \sum_{i=1}^N (\alpha_i - \alpha_i^*)(y_i - w^T x_i - b - \epsilon - \xi_i) - \sum_{i=1}^N (\alpha_i + \alpha_i^*)(\xi_i + \xi_i^*)

Kondisi Karush-Kuhn-Tucker (KKT)

Menerapkan kondisi KKT pada fungsi Lagrange menghasilkan masalah dual, yang melibatkan memaksimalkan fungsi objektif dual berikut terhadap pengganda Lagrange $\alpha$ dan $\alpha^*$ :

\max_{\alpha, \alpha^*} \Bigg( -\frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N (\alpha_i - \alpha_i^*)(\alpha_j - \alpha_j^*) y_i y_j x_i^T x_j + \sum_{i=1}^N (\alpha_i + \alpha_i^*) y_i - \epsilon \sum_{i=1}^N (\alpha_i + \alpha_i^*) \Bigg)

Dengan kendala:

\begin{aligned} \sum_{i=1}^N (\alpha_i - \alpha_i^*) &= 0 \\ \alpha_i, \alpha_i^* &\in [0, C], \quad i = 1, \dots, N \end{aligned}

dimana $K(x_i,x_j)$ adalah fungsi kernel yang menghitung hasil perkalian dalam antara dua vektor fitur input dalam ruang fitur yang diubah.

Trick Kernel

Fungsi kernel

Dalam SVR non-linier, kita menggunakan kernel trick untuk memetakan data input ke ruang dimensi yang lebih tinggi, di mana fungsi linear dapat digunakan untuk mendekati hubungan non-linier. Fungsi kernel adalah pengukuran kesamaan yang menghitung hasil perkalian dalam antara dua vektor fitur input dalam ruang transformasi:

K(x_i, x_j) = \phi(x_i)^T \phi(x_j)

Dimana $\phi(x_i)$ dan $\phi(x_j)$ adalah pemetaan vektor fitur input $x_i$ dan $x_j$ ke ruang fitur yang diubah.

Kernel Populer di SVR

Beberapa fungsi kernel populer yang digunakan dalam SVR meliputi:

Kernel linier

K(x_i, x_j) = x_i^T x_j

Kernel polinomial

K(x_i, x_j) = (x_i^T x_j + c)^d

Kernel fungsi basis radial (RBF)

K(x_i, x_j) = \exp(-\gamma ||x_i - x_j||^2)

Kernel sigmoidal

K(x_i, x_j) = \tanh(\kappa x_i^T x_j + c)

Dengan mengganti hasil perkalian dalam $x_i^Tx_j$ dengan fungsi kernel $K(x_i,x_j)$ dalam formulasi dual masalah SVR, kita dapat mengatasi hubungan non-linier secara efisien tanpa secara eksplisit mentransformasikan data input.

Implementasi SVR di Python

Pada bab ini, saya akan mengimplementasikan SVR menggunakan Python dan perpustakaan scikit-learn. Kita akan menggunakan kumpulan data Iris dan memvisualisasikan Support Vector dengan berbagai fungsi kernel.

Pertama, mari muat kumpulan data Iris dan persiapkan untuk regresi.

python

from sklearn import datasets
from sklearn.model_selection import train_test_split

iris = datasets.load_iris()
X = iris.data[:, :2]  # Use the first two features.
y = iris.data[:, 2]   # Use the third feature as the target.

# Split the dataset into a training set and a test set.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

Selanjutnya, mari latih model SVR dengan berbagai fungsi kernel.

python

from sklearn.svm import SVR

# Initialize SVR models with different kernels.
svr_linear = SVR(kernel='linear', C=1)
svr_poly = SVR(kernel='poly', C=1, degree=3)
svr_rbf = SVR(kernel='rbf', C=1, gamma='auto')

# Train the SVR models.
svr_linear.fit(X_train, y_train)
svr_poly.fit(X_train, y_train)
svr_rbf.fit(X_train, y_train)

Untuk memvisualisasikan Support Vector, kita akan membuat plot sebaran titik data dan menyoroti Support Vector.

python

import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np

sns.set(style="darkgrid")

def plot_support_vectors(svr_model, X, y, title, ax):
    h = .02  # step size in the mesh
    # Create a mesh to plot in.
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                         np.arange(y_min, y_max, h))

    # Predict target values for the mesh.
    Z = svr_model.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)

    # Plot the contour of the predictions.
    ax.contourf(xx, yy, Z, alpha=0.8)
    scatter = ax.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', marker='o', s=50)
    ax.set_title(title)
    ax.legend(*scatter.legend_elements())

fig, axes = plt.subplots(1, 3, figsize=(18, 6))
plot_support_vectors(svr_linear, X_train, y_train, 'SVR with Linear Kernel', axes[0])
plot_support_vectors(svr_poly, X_train, y_train, 'SVR with Polynomial Kernel', axes[1])
plot_support_vectors(svr_rbf, X_train, y_train, 'SVR with RBF Kernel', axes[2])

plt.show()

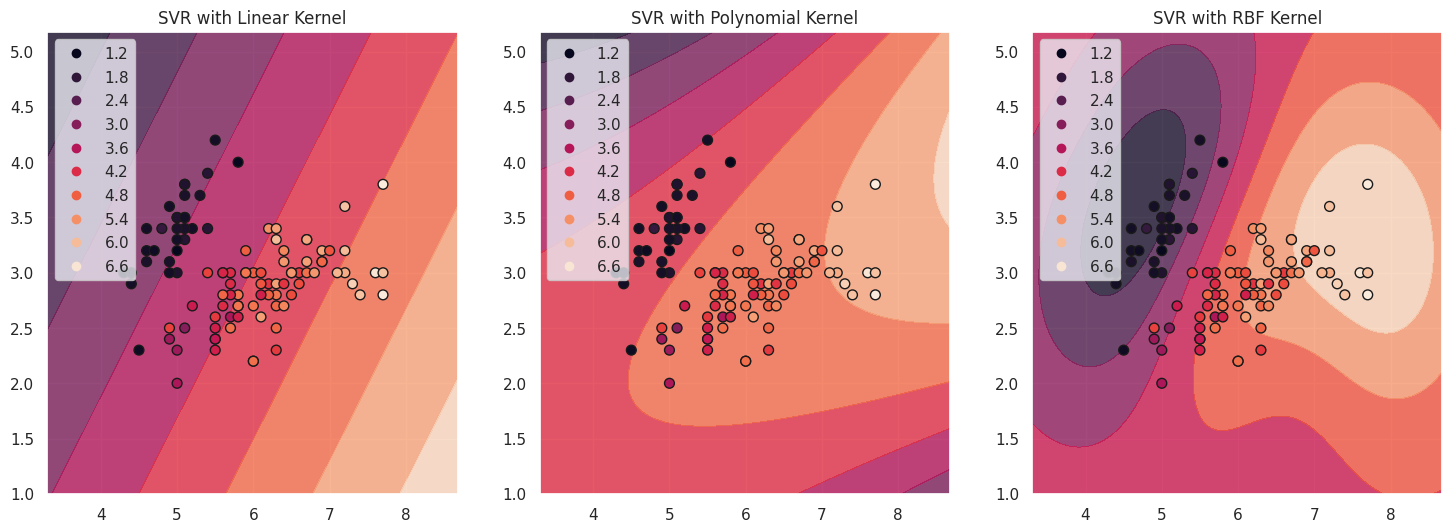
SVR with various kernel function

Support Vector adalah titik data yang berada di dalam atau pada batas margin. Mereka sangat penting dalam menentukan posisi hiperplane dan memiliki pengaruh yang signifikan pada prediksi model. Pada grafik di atas, Support Vector direpresentasikan oleh titik-titik pada garis kontur fungsi aproksimasi untuk setiap kernel. Titik-titik ini memainkan peran penting dalam menentukan bentuk batas keputusan dan kinerja keseluruhan model SVR.

Untuk mengevaluasi kinerja model SVR kita dengan kernel yang berbeda, kita dapat menghitung rata-rata kesalahan kuadrat (MSE) dan skor R-kuadrat pada set tes.

python

from sklearn.metrics import mean_squared_error, r2_score

def evaluate_model(svr_model, X_test, y_test):
    y_pred = svr_model.predict(X_test)
    mse = mean_squared_error(y_test, y_pred)
    r2 = r2_score(y_test, y_pred)
    return mse, r2

mse_linear, r2_linear = evaluate_model(svr_linear, X_test, y_test)
mse_poly, r2_poly = evaluate_model(svr_poly, X_test, y_test)
mse_rbf, r2_rbf = evaluate_model(svr_rbf, X_test, y_test)

print("Linear kernel: MSE = {:.2f}, R^2 = {:.2f}".format(mse_linear, r2_linear))
print("Polynomial kernel: MSE = {:.2f}, R^2 = {:.2f}".format(mse_poly, r2_poly))
print("RBF kernel: MSE = {:.2f}, R^2 = {:.2f}".format(mse_rbf, r2_rbf))

Linear kernel: MSE = 0.31, R^2 = 0.91
Polynomial kernel: MSE = 0.54, R^2 = 0.84
RBF kernel: MSE = 0.30, R^2 = 0.91

Ini akan menghasilkan rata-rata kesalahan kuadrat dan skor R-kuadrat untuk masing-masing model SVR. Dengan membandingkan metrik ini, kita dapat menentukan kernel mana yang memberikan hasil terbaik untuk data kita.