Apa yang dimaksud dengan fungsi loss?

Dalam machine learning, fungsi loss adalah fungsi untuk menghitung ukuran perbedaan antara "nilai prediksi" yang dihasilkan oleh model dan "nilai yang benar" yang sebenarnya. Dengan kata lain, loss function adalah indikator "buruknya" model, yaitu, seberapa buruk model tersebut cocok dengan data. Dalam melatih neural network, model dioptimalkan dengan mencari parameter (weight dan bias) yang meminimalkan loss function.

Ada berbagai macam fungsi kerugian. Berikut ini adalah contoh-contohnya

• Mean Squared Error (MSE)
• Mean Absolute Error (MAE)
• Root Mean Square Error (RMSE)
• Logarithmic Mean Square Error (MSLE)
• Cross-entropy error
• Huber Loss
• Poisson Loss

Dalam artikel ini, saya akan memperkenalkan Mean Square Error dan Cross Entropy Error.

Mean Square Error (MSE)

MSE adalah perbedaan antara nilai output dan nilai yang benar dikuadratkan dan dijumlahkan di atas semua neuron lapisan output. Kesalahan kuadrat rata-rata didefinisikan oleh persamaan berikut di mana E adalah kesalahan, y_k adalah setiap nilai output di lapisan output dan t_k adalah nilai jawaban yang benar.

MSE sering digunakan dalam masalah regresi karena cocok untuk kasus-kasus di mana jawaban atau output yang benar adalah angka kontinu.

Dengan menggunakan Python, mean square error dapat diimplementasikan sebagai berikut.

def square_sum(y, t):
    return 1.0/2.0 * np.sum(np.square(y - t))

Mari kita uji fungsi ini dengan contoh pengenalan digit tulisan tangan. Pertama, siapkan nilai output berikut untuk fungsi softmax.

y = np.array([0.1, 0,6, 0,2, 0.05, 0.05, 0, 0, 0, 0, 0])

Output dari fungsi softmax dapat diinterpretasikan sebagai probabilitas, yang berarti bahwa probabilitas "0" adalah 0,1 dan probabilitas "1" adalah 0,6.

Selanjutnya, kita menyiapkan data jawaban yang benar. Di sini, kita menyiapkan data jawaban yang benar untuk kasus-kasus di mana jawaban yang benar untuk pengenalan digit tulisan tangan masing-masing adalah "0" dan "1".

t1 = np.array([1, 0, 0, 0, 0, 0, 0, 0, 0, 0])
t2 = np.array([0, 1, 0, 0, 0, 0, 0, 0, 0, 0])

Data yang benar adalah representasi one-hot, di mana label yang benar diwakili oleh 1 dan semua label lainnya diwakili oleh 0.

MSE dihitung dengan menggunakan nilai output dan data jawaban yang benar.

import numpy as np

def square_sum(y, t):
    return 1.0/2.0 * np.sum(np.square(y - t))

y = np.array([0.1, 0.6, 0.2, 0.05, 0.05, 0, 0, 0, 0, 0])

t1 = np.array([1, 0, 0, 0, 0, 0, 0, 0, 0, 0])
t2 = np.array([0, 1, 0, 0, 0, 0, 0, 0, 0, 0])

print('y and t1:', square_sum(y, t1))
print('y and t2:', square_sum(y, t2))

y and t1: 0.6074999999999999
y and t2: 0.10750000000000003

Karena output y memiliki probabilitas tertinggi adalah "1", kita melihat bahwa error dengan t2, dimana "1" adalah label yang benar, lebih kecil.

Cross-Entropy Error

Cross-entropy error adalah ukuran perbedaan antara dua distribusi dan sering digunakan dalam masalah klasifikasi. Cross-entropy error dinyatakan dengan persamaan berikut.

Nilai jawaban yang benar dalam masalah klasifikasi adalah representasi satu-hot, di mana tingkat jawaban yang benar diwakili oleh 1 dan semua nilai lainnya diwakili oleh 0. Oleh karena itu, hanya istilah dengan $t_k $ 1 dalam $\sum $ di sisi kanan yang akan mempengaruhi kesalahan, dan efek istilah dengan $t_k $ 0 akan diabaikan.

Mari kita pikirkan tentang \log (y_k). Logaritma natural \log x memiliki properti yang menjadi "0" ketika x adalah 1 dan menjadi sangat kecil ketika x mendekati 0. Mengambil nilai absolut dari logaritma natural, grafik -\log x terhadap output y dari neural network adalah sebagai berikut.

%matplotlib inline

import matplotlib.pyplot as plt
y = np.arange(0, 1.01, 0.01)
delta = 1e-7
loss = -np.log(y + delta)
plt.plot(y, loss)
plt.xlim(0, 1)
plt.xlabel('x')
plt.ylim(0, 5)
plt.ylabel('- log x')
plt.show()

-\log x adalah 0 ketika x adalah 1 dan tumbuh besar tak terhingga ketika x mendekati 0. Dengan kata lain, semakin dekat output ke jawaban yang benar, semakin dekat kesalahannya ke 0, dan semakin jauh outputnya jauh dari jawaban yang benar, semakin jauh kesalahannya dari 0. Dengan demikian, kesalahan cross-entropy menggunakan properti logaritma natural untuk menurunkan fungsi kerugian.

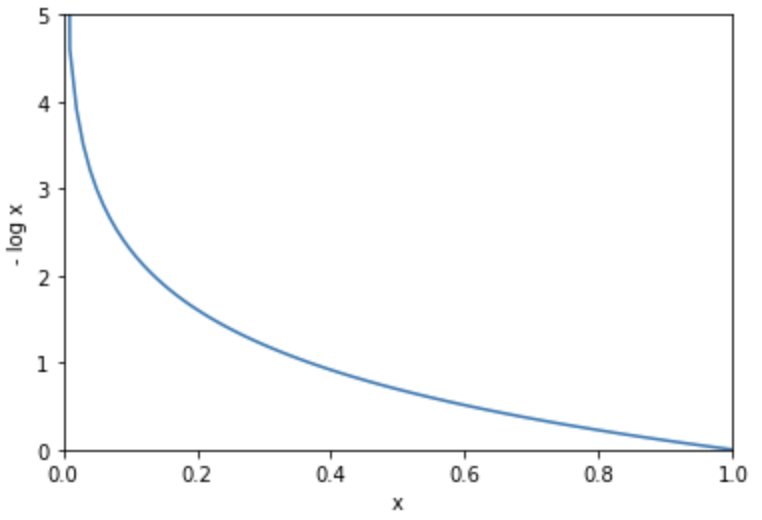
Cross-entropy memiliki keuntungan dari kecepatan belajar yang cepat ketika isolasi antara output dan nilai yang benar besar. Seperti disebutkan di atas, pembelajaran cepat dalam kasus seperti itu karena kesalahan tumbuh tak terhingga ketika output terisolasi dari jawaban yang benar.

Cross-entropy error dapat diimplementasikan dalam Python sebagai berikut.

import numpy as np

def cross_entropy(y, t):
    return - np.sum(t * np.log(y + 1e-7))

Alasan untuk menambahkan nilai menit 1e-7 ke y adalah untuk mencegah isi dari fungsi log menjadi nol dan logaritma natural menyimpang ke tak terhingga.

Hitung cross-entropy error dengan menggunakan output dan data yang benar yang digunakan dalam contoh MSE.

import numpy as np

def cross_entropy(y, t):
    return - np.sum(t * np.log(y + 1e-7))

y = np.array([0.1, 0.6, 0.2, 0.05, 0.05, 0, 0, 0, 0, 0])

t1 = np.array([1, 0, 0, 0, 0, 0, 0, 0, 0, 0])
t2 = np.array([0, 1, 0, 0, 0, 0, 0, 0, 0, 0])

print('y and t1:', cross_entropy(y, t1))
print('y and t2:', cross_entropy(y, t2))

y and t1: 2.302584092994546
y and t2: 0.510825457099338

Kita bisa mengekspresikan kesalahan antara output dan data yang benar sebagai fungsi kerugian!