2022-10-20

Support Vector Machine (SVM)

Machine Learning

Classification

Python

sklearn

Apa itu Support Vector Machine (SVM)

Support Vector Machine (SVM) adalah algoritma pembelajaran mesin yang kuat digunakan untuk klasifikasi. SVM adalah pengklasifikasi linear biner non-probabilistik yang mencoba untuk menemukan hiperplane terbaik di ruang fitur yang memisahkan titik data dari kelas yang berbeda dengan margin maksimum. Hiperplane dipilih sedemikian rupa sehingga memisahkan titik data secara optimal, dan margin didefinisikan sebagai jarak antara hiperplane dan titik data terdekat dari setiap kelas.

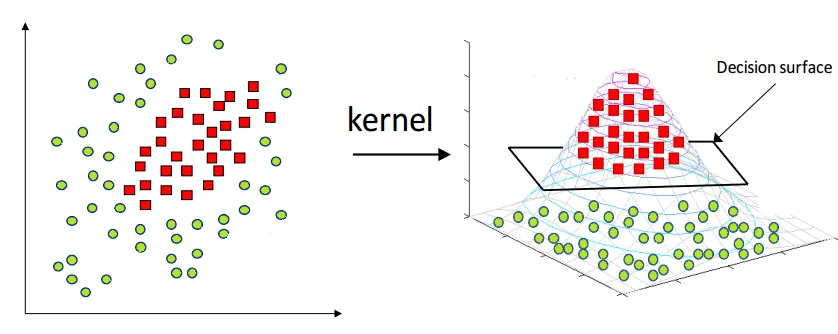
Selain data yang dapat dipisahkan secara linear, SVM juga dapat menangani data yang tidak dapat dipisahkan secara linear dengan menggunakan trik kernel. Trik kernel melibatkan pemetaan data input ke dalam ruang fitur dimensi yang lebih tinggi di mana data dapat dipisahkan secara linear. SVM mencoba untuk menemukan hiperplane optimal di ruang fitur dimensi yang lebih tinggi ini untuk memisahkan titik data.

Konsep Dasar dan Istilah

Hyperplane
Hyperplane adalah objek geometri yang menggeneralisasi konsep garis lurus (di 2D) atau bidang (di 3D) ke dalam ruang dimensi yang lebih tinggi. Dalam ruang n-dimensi, hyperplane didefinisikan sebagai objek (n-1)-dimensi.

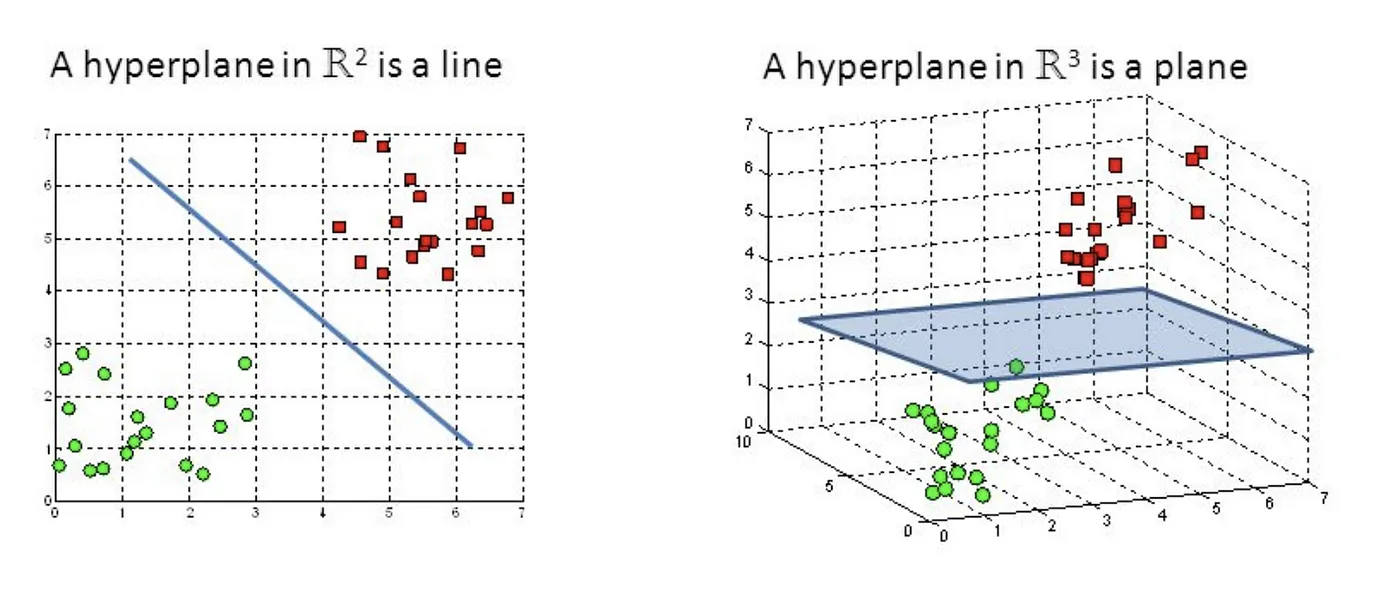
Hyperplane
Support Vector Machine — Introduction to Machine Learning Algorithms

Margin
Margin adalah jarak antara hyperplane pemisah dan titik data terdekat dari kelas yang berbeda. Tujuan SVM adalah untuk menemukan hyperplane yang memaksimalkan margin ini, memberikan kemampuan generalisasi yang lebih baik.
Support Vectors
Support vector adalah titik data yang terletak paling dekat dengan hyperplane pemisah dan berkontribusi dalam menentukan margin. Titik data ini sangat penting dalam menentukan posisi hyperplane.

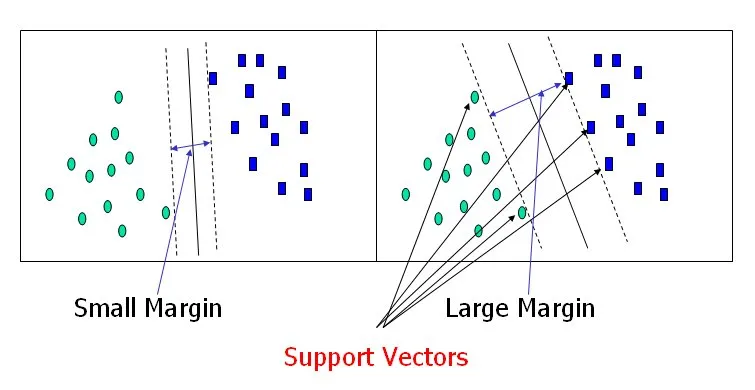
Support Vector Machine — Introduction to Machine Learning Algorithms

Linear Separability
Dataset dikatakan dapat dipisahkan secara linier jika terdapat hyperplane yang dapat memisahkan sempurna titik data dari kelas yang berbeda.
Kernel Function
Fungsi kernel adalah fungsi matematika yang memetakan titik data asli ke dalam ruang fitur yang lebih tinggi, memungkinkan algoritma SVM untuk menangani data yang tidak dapat dipisahkan secara linier.

What is the kernel trick? Why is it important?

Matematika di Balik SVM

Linear Separability dan Hyperplane

Diberikan dataset dengan fitur vektor n-dimensi, hyperplane didefinisikan sebagai objek (n-1)-dimensi yang dapat direpresentasikan oleh persamaan:

\boldsymbol{w} \cdot \boldsymbol{x} + b = 0

di mana $\boldsymbol{w}$ adalah vektor bobot, $\boldsymbol{x}$ adalah vektor fitur, dan $b$ adalah istilah bias. Tujuan dari SVM adalah untuk menemukan hyperplane yang optimal yang memisahkan titik data dari kelas yang berbeda.

Maksimasi Margin

Margin ( $M$ ) adalah jarak antara hyperplane dan titik data terdekat (support vector) dari kelas yang berbeda. Untuk suatu titik data $\boldsymbol{x}_i$ dengan label kelas $y_i \in {-1, 1}$ , persamaan hyperplane dapat ditulis sebagai:

y_i(\boldsymbol{w} \cdot \boldsymbol{x}_i + b) = 1

Jarak dari titik data $\boldsymbol{x}_i$ ke hyperplane diberikan oleh:

\frac{(\boldsymbol{w} \cdot \boldsymbol{x}_i) + b}{||\boldsymbol{w}||}

Karena yang diinginkan adalah margin, yaitu jarak terkecil antara hyperplane dan titik data dari kelas yang berbeda, maka diperoleh:

M = \frac{1}{||\boldsymbol{w}||}

Tujuan dari SVM adalah untuk memaksimalkan margin $M$ sambil mempertahankan kendala klasifikasi.

y_i(\boldsymbol{w} \cdot \boldsymbol{x}_i + b) \geq 1, \quad \forall i

Maksimalkan margin $M$ sama dengan meminimalkan norma Euclidean kuadrat dari vektor bobot $||\boldsymbol{w}||^2$ .

Masalah Dual dan Multiplier Lagrange

Untuk menyelesaikan masalah optimasi terbatas, kita dapat menggunakan multiplier Lagrange. Lagrangian untuk masalah optimasi SVM dapat ditulis sebagai:

\mathcal{L}(\boldsymbol{w}, b, \boldsymbol{\alpha}) = \frac{1}{2} ||\boldsymbol{w}||^2 - \sum_{i=1}^{N} \alpha_i \left[ y_i(\boldsymbol{w} \cdot \boldsymbol{x}_i + b) - 1 \right]

di mana $N$ adalah jumlah titik data, dan $\boldsymbol{\alpha}$ adalah vektor multiplier Lagrange.

Kita perlu meminimalkan $\mathcal{L}(\boldsymbol{w}, b, \boldsymbol{\alpha})$ terhadap $\boldsymbol{w}$ dan $b$ dan memaksimalkannya terhadap $\boldsymbol{\alpha}$ . Syarat titik saddle menghasilkan:

\frac{\partial \mathcal{L}}{\partial \boldsymbol{w}} = \boldsymbol{w} - \sum_{i=1}^{N} \alpha_i y_i \boldsymbol{x}_i = 0

dan

\frac{\partial \mathcal{L}}{\partial b} = \sum_{i=1}^{N} \alpha_i y_i = 0

Mengganti kondisi ini ke dalam Lagrangian, kita mendapatkan masalah optimasi ganda:

\max_{\boldsymbol{\alpha}} \left[ \sum_{i=1}^{N} \alpha_i - \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_i \alpha_j y_i y_j (\boldsymbol{x}_i \cdot \boldsymbol{x}_j) \right]

terbatas pada kendala:

\alpha_i \geq 0, \quad \forall i

dan

\sum_{i=1}^{N} \alpha_i y_i = 0

Masalah dual ini adalah masalah pemrograman kuadrat, yang dapat dipecahkan menggunakan teknik optimasi seperti algoritma Sequential Minimal Optimization (SMO) atau metode berbasis gradien.

Kernel Trick

Dalam kasus di mana data tidak dapat dipisahkan secara linier, SVM menggunakan kernel trick untuk mentransformasikan data ke dalam ruang dimensi yang lebih tinggi di mana data tersebut dapat dipisahkan secara linier. Fungsi kernel $K(\boldsymbol{x}_i, \boldsymbol{x}_j)$ digunakan untuk memetakan titik data asli ke dalam ruang fitur baru, memungkinkan algoritma SVM untuk menemukan hyperplane pemisah yang optimal. Masalah dual sekarang menjadi:

\max_{\boldsymbol{\alpha}} \left[ \sum_{i=1}^{N} \alpha_i - \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_i \alpha_j y_i y_j K(\boldsymbol{x}_i, \boldsymbol{x}_j) \right]

terbatas pada kendala yang sama seperti sebelumnya. Beberapa fungsi kernel populer meliputi kernel linier, kernel polinomial, kernel fungsi basis radial (RBF), dan kernel sigmoid.

Setelah menyelesaikan masalah dual, vektor bobot $\boldsymbol{w}$ dapat dihitung sebagai:

\boldsymbol{w} = \sum_{i=1}^{N} \alpha_i y_i \phi(\boldsymbol{x}_i)

di mana $\phi(\boldsymbol{x}_i)$ adalah vektor fitur yang dipetakan ke dalam ruang dimensi yang lebih tinggi. Istilah bias $b$ dapat dihitung menggunakan support vector $\boldsymbol{x}_s$ apa pun:

b = \frac{1}{y_s} - \sum_{i=1}^{N} \alpha_i y_i K(\boldsymbol{x}_i, \boldsymbol{x}_s)

Fungsi keputusan untuk titik data baru $\boldsymbol{x}^*$ kemudian diberikan oleh:

f(\boldsymbol{x}^*) = \operatorname{sign} \left( \sum_{i=1}^{N} \alpha_i y_i K(\boldsymbol{x}_i, \boldsymbol{x}^*) + b \right)

Kernel trick memungkinkan SVM untuk menangani data yang tidak dapat dipisahkan secara linier dan menyediakan cara yang fleksibel untuk menggabungkan pengetahuan domain ke dalam algoritma dengan memilih fungsi kernel yang tepat.

Implementasi SVM dengan Dataset Iris

Pada bab ini, saya akan mengimplementasikan SVM menggunakan Python dan scikit-learn. Kita akan menggunakan dataset Iris untuk mengilustrasikan kemampuan klasifikasi SVM dengan berbagai kernel.

Pertama, mari impor perpustakaan yang diperlukan dan memuat dataset Iris:

python

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix

# Load the Iris dataset
iris = datasets.load_iris()
X = iris.data[:, :2]  # We will only use the first two features for visualization purposes
y = iris.target

Kita akan membagi dataset menjadi set pelatihan dan pengujian, dan melatih model SVM dengan berbagai kernel:

python

# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Define the kernel names and types
kernels = {
    'Linear': 'linear',
    'Polynomial': 'poly',
    'RBF': 'rbf',
    'Sigmoid': 'sigmoid'
}

# Train and evaluate the SVM model with different kernels
for name, kernel in kernels.items():
    svm = SVC(kernel=kernel, C=1, degree=3, gamma='scale', coef0=0.0, shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape='ovr', break_ties=False, random_state=None)
    svm.fit(X_train, y_train)
    y_pred = svm.predict(X_test)
    accuracy = accuracy_score(y_test, y_pred)
    print(f'{name} Kernel SVM Accuracy: {accuracy:.2f}')

Linear Kernel SVM Accuracy: 0.80
Polynomial Kernel SVM Accuracy: 0.73
RBF Kernel SVM Accuracy: 0.80
Sigmoid Kernel SVM Accuracy: 0.29

Sekarang, mari buat fungsi untuk memvisualisasikan batas keputusan untuk berbagai kernel dan plot hasilnya:

python

def plot_svm_decision_boundary(svm, X, y, kernel, ax):
    h = .02  # Step size in the mesh
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

    Z = svm.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)

    ax.contourf(xx, yy, Z, alpha=0.8, cmap=plt.cm.coolwarm)
    scatter = ax.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', marker='o', s=50, cmap=plt.cm.coolwarm)
    ax.set_xlabel('Feature 1')
    ax.set_ylabel('Feature 2')
    ax.set_title(f'{kernel} Kernel SVM')
    ax.legend(*scatter.legend_elements(), title="Classes")

# Create a figure and subplots for each kernel
fig, axes = plt.subplots(2, 2, figsize=(12, 12))
axes = axes.ravel()

# Plot the decision boundaries
for i, (name, kernel) in enumerate(kernels.items()):
    svm = SVC(kernel=kernel, C=1, degree=3, gamma='scale', coef0=0.0, shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape='ovr', break_ties=False, random_state=None)
    svm.fit(X_train, y_train)
    plot_svm_decision_boundary(svm, X_train, y_train, name, axes[i])

# Adjust plot layout and show the figure
plt.tight_layout()
plt.show()

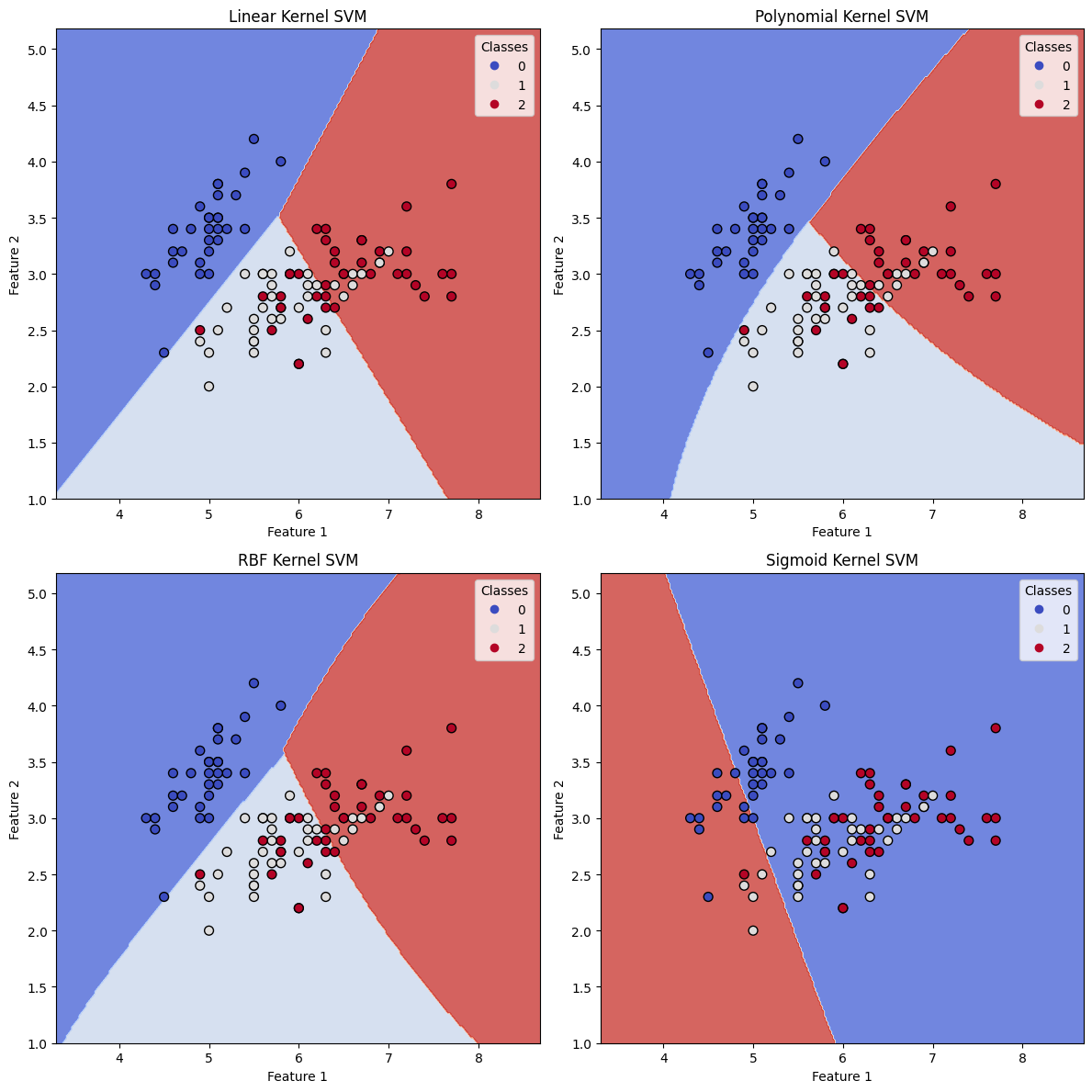
SVM plot

Dengan menjalankan kode di atas, kita memperoleh empat plot yang menunjukkan batas keputusan dari model SVM dengan kernel yang berbeda. Plot mengilustrasikan bagaimana setiap kernel menghasilkan batas keputusan yang berbeda, yang pada gilirannya mempengaruhi hasil klasifikasi.

Kernel Linier menghasilkan batas keputusan linier, yang mungkin tidak cocok untuk dataset kompleks dengan pola nonlinier.
Kernel Polinomial memungkinkan fleksibilitas yang lebih besar dengan membuat batas keputusan melengkung, yang dapat lebih baik menyesuaikan data saat pemisahan linier tidak mungkin. Derajat polinomial dapat disesuaikan untuk mengontrol kompleksitas batas keputusan.
Kernel RBF (Fungsi Basis Radial) adalah pilihan yang sangat populer untuk banyak masalah klasifikasi, karena dapat menangani pola yang kompleks dan nonlinier dalam data. Batas keputusan sangat halus dan beradaptasi dengan baik dengan struktur dasar dari dataset.
Kernel Sigmoid juga dapat membuat batas keputusan nonlinier, tetapi umumnya kurang populer dibandingkan kernel RBF.

Dari skor akurasi dan plot, kita dapat mengamati bagaimana berbagai fungsi kernel memengaruhi kinerja klasifikasi SVM. Tergantung pada sifat dataset dan pola dasarnya, kernel yang tepat harus dipilih untuk mencapai hasil klasifikasi terbaik.