Apa itu Koefisien Determinasi (R-squared)

Koefisien determinasi, atau R^2, adalah ukuran statistik yang digunakan dalam analisis regresi untuk mengevaluasi kecocokan model. Ini menunjukkan proporsi variasi dalam variabel dependen yang dapat dijelaskan oleh variabel independen. R^2 memiliki rentang nilai antara 0 hingga 1, dengan 0 artinya tidak ada variasi dalam variabel dependen yang dapat dijelaskan oleh variabel independen dan 1 artinya semua variasi dapat dijelaskan oleh variabel independen.

Rumus untuk R^2 adalah:

di mana,

• y_i adalah nilai teramati dari variabel dependen untuk titik data ke-i.
• \hat{y_i} adalah nilai diprediksi dari variabel dependen untuk titik data ke-i.
• \bar{y} adalah nilai mean dari variabel dependen.

R-squared dan Kecocokan Model

Kecocokan model adalah ukuran seberapa baik model statistik sesuai dengan data yang diamati. Nilai R^2 yang lebih tinggi menunjukkan bahwa model statistik tersebut lebih sesuai dengan data, karena dapat menjelaskan proporsi variasi yang lebih besar dalam variabel dependen. Namun, perlu diingat bahwa nilai R^2 yang tinggi tidak selalu menunjukkan adanya hubungan sebab-akibat antara variabel independen dan dependen, dan R^2 tidak boleh menjadi satu-satunya kriteria untuk menilai kinerja model.

R-squared dan Koefisien Korelasi

Koefisien korelasi (r) adalah ukuran kekuatan dan arah hubungan linier antara dua variabel. Rentang nilainya dari -1 (korelasi negatif sempurna) hingga 1 (korelasi positif sempurna), dengan nilai 0 menunjukkan tidak ada korelasi. Dalam regresi linier sederhana, R^2 sama dengan kuadrat dari koefisien korelasi, yang berarti menunjukkan proporsi variasi dalam variabel dependen yang dapat dijelaskan oleh hubungan linier dengan variabel independen. Rumus untuk menghitung R^2 dalam regresi linier sederhana adalah:

Adjusted R-squared

Adjusted R^2 adalah modifikasi dari R^2 yang mempertimbangkan jumlah variabel independen dan ukuran sampel. Ini sangat berguna dalam analisis regresi ganda, di mana penambahan variabel independen dapat meningkatkan nilai R^2, membuat model tampak lebih cocok daripada yang sebenarnya. Rumus untuk adjusted R^2 adalah:

di mana n adalah ukuran sampel dan k adalah jumlah variabel independen.

Adjusted R^2 memperhitungkan penambahan variabel independen yang tidak memberikan kontribusi signifikan terhadap varians yang dijelaskan dalam variabel dependen, sehingga membantu mencegah overfitting dan membantu dalam pemilihan model.

Menghitung dan Menginterpretasikan R-squared Menggunakan Python

Dalam bab ini, saya akan menunjukkan bagaimana menghitung R-squared menggunakan Python dan kumpulan data Perumahan California.

Pertama, kita akan mengimpor perpustakaan yang dibutuhkan dan memuat kumpulan data Perumahan California, sebuah kumpulan data publik yang banyak digunakan untuk analisis regresi.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from sklearn.model_selection import train_test_split
from sklearn.datasets import fetch_california_housing

# Load the California Housing dataset
california = fetch_california_housing()
data = pd.DataFrame(california.data, columns=california.feature_names)
data['Price'] = california.target

Selanjutnya, kita akan melakukan analisis regresi linier menggunakan kelas LinearRegression dari scikit-learn dan menghitung nilai R-squared menggunakan fungsi r2_score. Kita akan membuat dua model regresi linier terpisah menggunakan variabel independen yang baik, MedInc, dan variabel independen yang buruk, HouseAge. Kemudian, kita akan menghitung nilai R-squared untuk kedua model.

# Good regression (MedInc vs. Price)
X_good = data[['MedInc']]
y_good = data['Price']

model_good = LinearRegression()
model_good.fit(X_good, y_good)

y_pred_good = model_good.predict(X_good)
r_squared_good = R-squared_score(y_good, y_pred_good)
print(f'R-squared (Good Regression - MedInc vs. Price): {r_squared_good:.2f}')

# Bad regression (HouseAge vs. Price)
X_bad = data[['HouseAge']]
y_bad = data['Price']

model_bad = LinearRegression()
model_bad.fit(X_bad, y_bad)

y_pred_bad = model_bad.predict(X_bad)
r_squared_bad = R-squared_score(y_bad, y_pred_bad)
print(f'R-squared (Bad Regression - HouseAge vs. Price): {r_squared_bad:.2f}')

R-squared (Good Regression - MedInc vs. Price): 0.47
R-squared (Bad Regression - HouseAge vs. Price): 0.01

Seperti yang diharapkan, nilai R-squared untuk regresi yang baik (MedInc vs. Price) lebih tinggi, menunjukkan kecocokan yang lebih baik untuk data. Sebaliknya, nilai R-squared untuk regresi yang buruk (HouseAge vs. Price) jauh lebih rendah, menunjukkan bahwa variabel HouseAge tidak memberikan kecocokan yang baik untuk data.

Kita akan memvisualisasikan hubungan antara variabel dependen Price dan variabel independen yang baik MedInc, dan variabel independen yang buruk HouseAge.

# Good regression (MedInc vs. Price)
plt.figure(figsize=(10, 6))
sns.regplot(x='MedInc', y='Price', data=data, scatter_kws={'alpha': 0.3}, line_kws={'color': 'red'})
plt.title('Good Regression: MedInc vs. Price')
plt.xlabel('Median Income')
plt.ylabel('Price')
plt.show()

# Bad regression (HouseAge vs. Price)
plt.figure(figsize=(10, 6))
sns.regplot(x='HouseAge', y='Price', data=data, scatter_kws={'alpha': 0.3}, line_kws={'color': 'red'})
plt.title('Bad Regression: HouseAge vs. Price')
plt.xlabel('House Age')
plt.ylabel('Price')
plt.show()

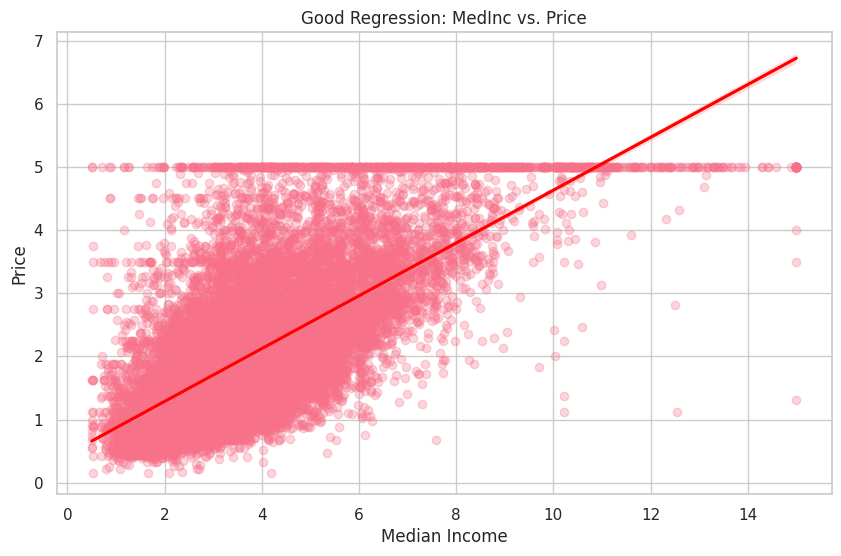
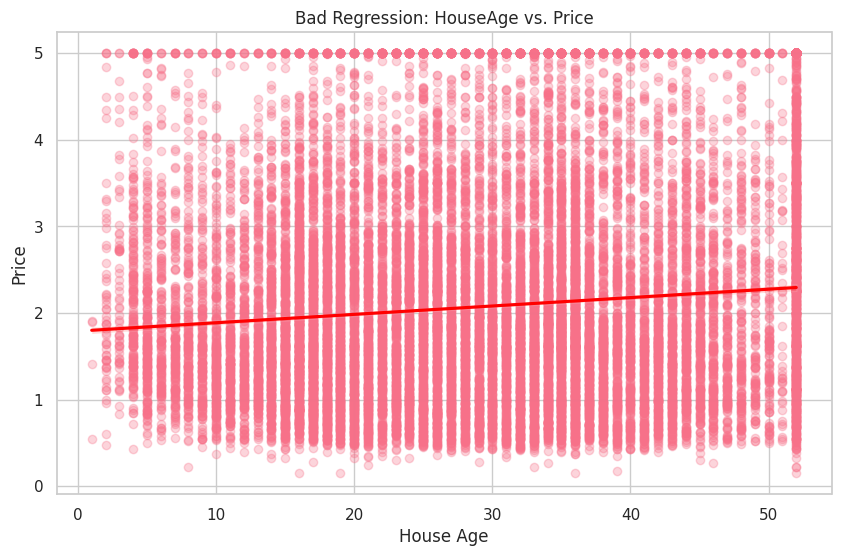
Pada plot pertama, Anda dapat melihat hubungan positif yang jelas antara MedInc dan Price. Di sisi lain, plot kedua menunjukkan hubungan yang lemah antara HouseAge dan Price.