2022-03-29

Koefisien Korelasi

Apa itu Koefisien Korelasi

Koefisien korelasi adalah ukuran numerik yang mengukur kekuatan dan arah hubungan linier antara dua variabel kontinu. Tujuannya utama adalah untuk menilai seberapa erat kedua variabel terkait dan memberikan wawasan tentang sifat asosiasi mereka. Bab ini lebih mendalam membahas dua koefisien korelasi yang paling umum digunakan: koefisien korelasi Pearson ( $r$ ) dan koefisien korelasi rank Spearman ( $\rho$ ).

Koefisien Korelasi Pearson

Koefisien korelasi Pearson ( $r$ ) dihitung menggunakan formula berikut:

r = \frac{\sum*{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum*{i=1}^{n}(x*i - \bar{x})^2 \sum*{i=1}^{n}(y_i - \bar{y})^2}}

di mana:

$n$ adalah jumlah titik data berpasangan
$x_i$ dan $y_i$ adalah titik data individu
$\bar{x}$ dan $\bar{y}$ adalah rerata variabel $x$ dan $y

Koefisien Korelasi Rank Spearman

Koefisien korelasi rank Spearman ( $\rho$ ) dihitung menggunakan formula berikut:

\rho = 1 - \frac{6 \sum\_{i=1}^{n} d_i^2}{n(n^2 - 1)}

di mana:

$n$ adalah jumlah titik data berpasangan
$d_i$ adalah selisih antara peringkat $x_i$ dan $y_i$ yang sesuai

Interpretasi Korelasi

Nilai koefisien korelasi berkisar antara -1 hingga 1. Kekuatan dan arah korelasi dapat diinterpretasikan sebagai berikut:

-1 ≤ r < -0,7: Korelasi negatif yang kuat
-0,7 ≤ r < -0,3: Korelasi negatif yang sedang
-0,3 ≤ r < 0: Korelasi negatif yang lemah
0: Tidak ada korelasi
0 < r ≤ 0,3: Korelasi positif yang lemah
0,3 < r ≤ 0,7: Korelasi positif yang sedang
0,7 < r ≤ 1: Korelasi positif yang kuat

Hubungan antara Kovarians dan Koefisien Korelasi

Kovarians dan koefisien korelasi keduanya adalah ukuran hubungan antara dua variabel. Sementara kovarians memberikan informasi tentang arah hubungan (positif atau negatif), ia tidak memberikan informasi tentang kekuatan hubungan. Sebaliknya, koefisien korelasi tidak hanya menunjukkan arah hubungan tetapi juga mengindikasikan kekuatan hubungan pada skala standar antara -1 hingga 1.

Hubungan antara kovarians dan koefisien korelasi Pearson dapat dinyatakan sebagai berikut:

r = \frac{cov(x, y)}{s_x s_y}

di mana:

$r$ adalah koefisien korelasi Pearson
$cov(x, y)$ adalah kovarians antara $x$ dan $y$
$s_x$ dan $s_y$ adalah simpangan baku $x$ dan $y`, masing-masing

Dalam persamaan ini, koefisien korelasi Pearson diperoleh dengan membagi kovarians dengan hasil kali simpangan baku kedua variabel. Proses ini mengstandarisasi kovarians sehingga koefisien korelasi yang dihasilkan berada di antara -1 dan 1, sehingga lebih mudah menginterpretasikan kekuatan hubungan.

Keterbatasan dan Asumsi Koefisien Korelasi

Baik Pearson $r$ maupun Spearman $\rho$ memiliki beberapa keterbatasan dan asumsi yang harus dipertimbangkan saat menginterpretasikan nilainya:

Koefisien korelasi hanya mengukur kekuatan hubungan linier antara dua variabel; mereka tidak menyiratkan sebab-akibat.
Outlier atau nilai ekstrim dapat berpengaruh signifikan terhadap koefisien korelasi, yang dapat menyebabkan hasil yang menyesatkan. Penting untuk memvisualisasikan data menggunakan scatterplot untuk mengidentifikasi outlier dan menilai sifat sebenarnya dari hubungan tersebut.
Koefisien korelasi Pearson mengasumsikan bahwa kedua variabel diukur pada skala interval atau rasio dan bahwa hubungan antara keduanya adalah linier. Jika asumsi ini tidak terpenuhi, hasilnya dapat tidak akurat.
Spearman $\rho$ lebih tahan terhadap outlier dan hubungan nonlinier tetapi memerlukan setidaknya satu variabel diukur pada skala ordinal atau untuk hubungan yang monotonic.
Koefisien korelasi dapat sensitif terhadap ukuran sampel; ukuran sampel yang lebih kecil dapat menghasilkan korelasi yang lebih lemah, bahkan jika hubungan yang kuat ada. Penting untuk memastikan bahwa ukuran sampel cukup besar untuk mewakili populasi secara akurat.

Menghitung Koefisien Korelasi dengan Python

Dalam bab ini, saya akan menunjukkan bagaimana menghitung koefisien korelasi menggunakan Python.

Pertama, mari impor library yang diperlukan.

python

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

Untuk contoh ini, mari buat dataset contoh dengan tiga variabel: x, y, dan z. Kita akan menggunakan pandas untuk membuat DataFrame yang berisi data.

python

data = {
    'x': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
    'y': [2, 4, 6, 8, 10, 12, 14, 16, 18, 20],
    'z': [10, 9, 8, 7, 6, 5, 4, 3, 2, 1]
}

df = pd.DataFrame(data)

Kita dapat menggunakan metode corr() yang tersedia dalam pandas DataFrame untuk menghitung matriks korelasi untuk dataset kita. Koefisien korelasi Pearson digunakan secara default saat menggunakan metode corr() di pandas DataFrame.

correlation_matrix = df.corr()
print(correlation_matrix)

     x    y    z
x  1.0  1.0 -1.0
y  1.0  1.0 -1.0
z -1.0 -1.0  1.0

Untuk membuat matriks korelasi lebih menarik secara visual, kita akan menggunakan seaborn untuk membuat heatmap.

python

plt.figure(figsize=(10, 7))
sns.set(font_scale=1.2)
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', annot_kws={"size": 12})
plt.title("Correlation Matrix")
plt.show()

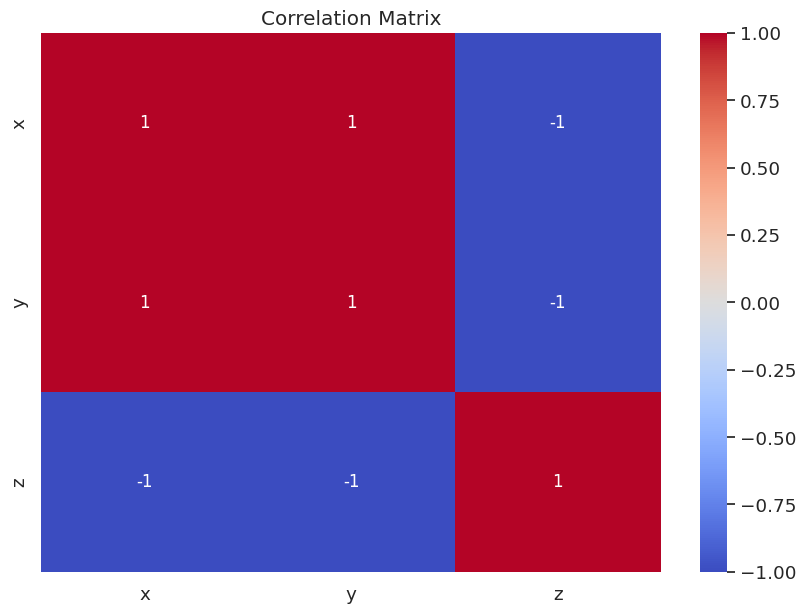
Correlation matrix

Matriks korelasi dan heatmap yang dihasilkan akan menampilkan koefisien korelasi untuk setiap pasangan variabel dalam dataset.

Koefisien korelasi antara x dan y adalah 1, menunjukkan korelasi positif yang kuat.
Koefisien korelasi antara x dan z adalah -1, menunjukkan korelasi negatif yang kuat.
Koefisien korelasi antara y dan z juga -1, menunjukkan korelasi negatif yang kuat.

Dengan menginterpretasikan koefisien korelasi, kita dapat memperoleh wawasan tentang hubungan antara variabel dalam dataset kita. Dalam contoh ini, kita dapat melihat bahwa x dan y memiliki hubungan linier positif yang kuat, sedangkan baik x dan z maupun y dan z memiliki hubungan linier negatif yang kuat.

Memahami Korelasi Secara Visual

Untuk menggambarkan data dengan berbagai koefisien korelasi, kita akan menghasilkan tiga dataset yang berbeda dengan tingkat korelasi yang bervariasi dan membuat scatterplot untuk setiap dataset.

Kode di atas menghasilkan tiga dataset yang berbeda:

python

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(42)

# Create dataset with a strong positive correlation
x1 = np.random.normal(50, 10, 100)
y1 = x1 * 1.2 + np.random.normal(0, 5, 100)

# Create dataset with a weak positive correlation
x2 = np.random.normal(50, 10, 100)
y2 = x2 * 0.2 + np.random.normal(0, 20, 100)

# Create dataset with no correlation
x3 = np.random.normal(50, 10, 100)
y3 = np.random.normal(50, 10, 100)

# Create scatterplots for each dataset
plt.figure(figsize=(18, 5))

plt.subplot(131)
plt.scatter(x1, y1)
plt.title("Strong Positive Correlation")
plt.xlabel("x1")
plt.ylabel("y1")

plt.subplot(132)
plt.scatter(x2, y2)
plt.title("Weak Positive Correlation")
plt.xlabel("x2")
plt.ylabel("y2")

plt.subplot(133)
plt.scatter(x3, y3)
plt.title("No Correlation")
plt.xlabel("x3")
plt.ylabel("y3")

plt.show()

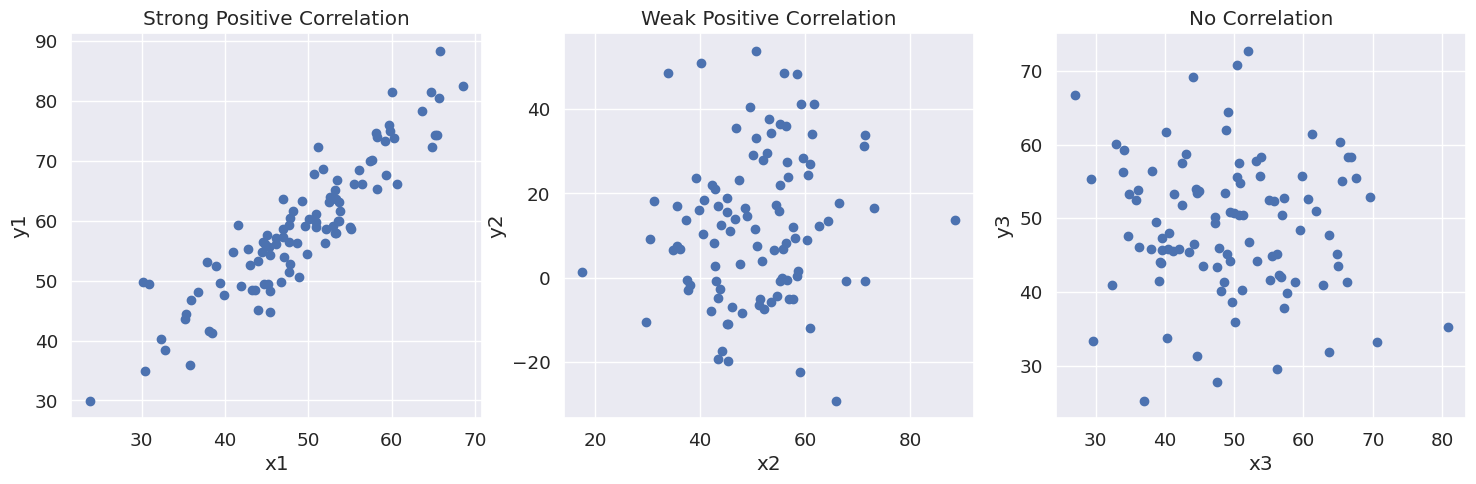
Correlation

Kode di atas menghasilkan tiga dataset yang berbeda:

Korelasi positif yang kuat: Dalam dataset ini, x1 dan y1 memiliki hubungan linier positif yang kuat, yang terlihat dalam scatterplot karena titik-titik terkumpul di sekitar garis dengan kemiringan positif.
Korelasi positif yang lemah: Dalam dataset ini, x2 dan y2 memiliki hubungan linier positif yang lemah. Scatterplot menunjukkan bahwa titik-titik tersebar di sekitar garis dengan kemiringan positif, tetapi penyebarannya jauh lebih besar dibandingkan dengan kasus korelasi positif yang kuat.
Tidak ada korelasi: Dalam dataset ini, x3 dan y3 tidak memiliki hubungan linier. Scatterplot menunjukkan bahwa titik-titik tersebar secara acak dan tidak mengikuti pola yang jelas.