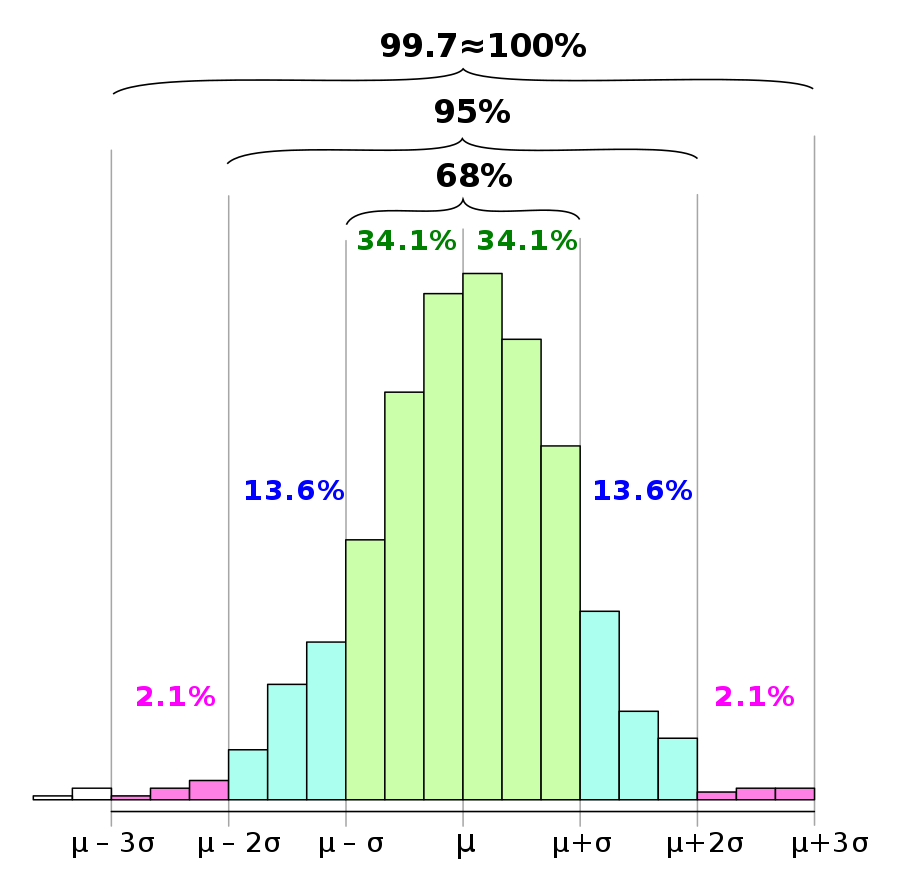
Aturan 68-95-99,7 dalam Distribusi Normal

Distribusi normal merupakan konsep dasar dalam bidang statistika dan probabilitas. Konsep ini memiliki berbagai aplikasi di berbagai disiplin ilmu, mulai dari ilmu sosial hingga ilmu alam dan rekayasa. Salah satu karakteristik penting dari distribusi normal adalah aturan 68-95-99,7 atau yang juga dikenal sebagai Aturan Empiris.

Memahami Aturan 68-95-99,7

Aturan Empiris didasarkan pada sifat kurva distribusi normal, yang simetris dan berbentuk lonceng. Dalam distribusi normal, mean, median, dan modus sama, dan kurva sepenuhnya ditentukan oleh mean (\mu) dan standar deviasi (\sigma). Standar deviasi adalah ukuran penyebaran atau sebaran dalam kumpulan data, menunjukkan seberapa dekat titik-titik data berkumpul di sekitar mean.

Aturan 68-95-99,7 menyatakan bahwa, dalam distribusi normal:

• Sekitar 68% data berada dalam satu standar deviasi (\mu\pm\sigma) dari mean.
• Sekitar 95% data berada dalam dua standar deviasi (\mu\pm2\sigma) dari mean.
• Sekitar 99,7% data berada dalam tiga standar deviasi (\mu\pm3\sigma) dari mean.

Persentase ini muncul dari sifat matematika distribusi normal dan berfungsi sebagai alat praktis untuk menganalisis data yang mengikuti distribusi ini.

68–95–99.7 rule

Memvisualisasikan Aturan 68-95-99,7

Dalam bab ini, saya akan menunjukkan cara memvisualisasikan aturan 68-95-99,7 menggunakan Python. Kita akan membuat kumpulan data yang terdistribusi normal dan membuat plot yang menyoroti persentase Aturan Empiris.

Berikut adalah kode:

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import norm

# Set the Seaborn style
sns.set(style="whitegrid")

# Parameters for the normal distribution
mean = 0
std_dev = 1
sample_size = 1000

# Generate the dataset
data = np.random.normal(mean, std_dev, sample_size)

plt.figure(figsize=(10, 6))

# Calculate the x values within each standard deviation range
x = np.linspace(mean - 3.5 * std_dev, mean + 3.5 * std_dev, 1000)
x1 = np.linspace(mean - std_dev, mean + std_dev, 1000)
x2 = np.linspace(mean - 2 * std_dev, mean + 2 * std_dev, 1000)
x3 = np.linspace(mean - 3 * std_dev, mean + 3 * std_dev, 1000)

# Get the corresponding y values for the normal distribution
y = norm.pdf(x, mean, std_dev)

# Plot the areas under the curve
plt.fill_between(x3, 0, norm.pdf(x3, mean, std_dev), color='darkblue', alpha=0.3, label='99.7%')
plt.fill_between(x2, 0, norm.pdf(x2, mean, std_dev), color='mediumblue', alpha=0.4, label='95%')
plt.fill_between(x1, 0, norm.pdf(x1, mean, std_dev), color='lightblue', alpha=0.5, label='68%')

# Customize the appearance
plt.plot(x, y, color='darkblue', linewidth=2)
plt.title('Visualizing the 68-95-99.7 Rule in Normal Distribution', fontsize=16)
plt.xlabel('Standard Deviations from the Mean', fontsize=14)
plt.ylabel('Density', fontsize=14)
plt.legend(title='Percentage', fontsize=12, title_fontsize=12)

# Display the plot
plt.show()

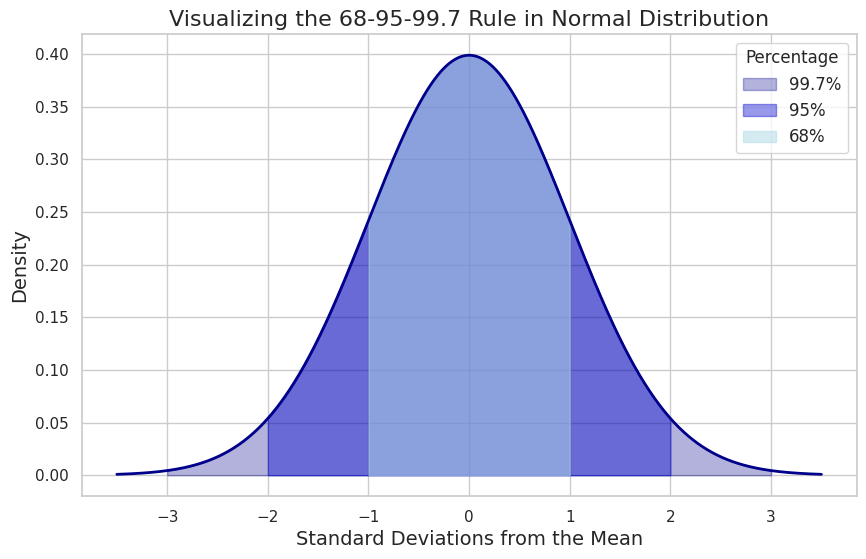
Kode ini akan menghasilkan plot yang mengilustrasikan aturan 68-95-99,7 dalam konteks distribusi normal. Area berbayang mewakili persentase data dalam satu, dua, dan tiga standar deviasi dari mean, sesuai dengan Aturan Empiris.