What is the exponential distribution

The exponential distribution is the probability distribution that the next time x that occurs on average \lambda times per unit time follows. The exponential distribution is used in the following example.

• A call center where the phone rings an average of 20 times per hour, and the time until the next call rings
• Time until the next occurrence of a disaster that occurs once every two years

The probability density function of the exponential distribution can be expressed as follows:

Where \lambda is the average number of times the event occurs in unit time and x is the period of time until the event occurs.

The exponential distribution of \lambda for \frac{1}{6}, \frac{1}{2}, 1, and 2 is as follows.

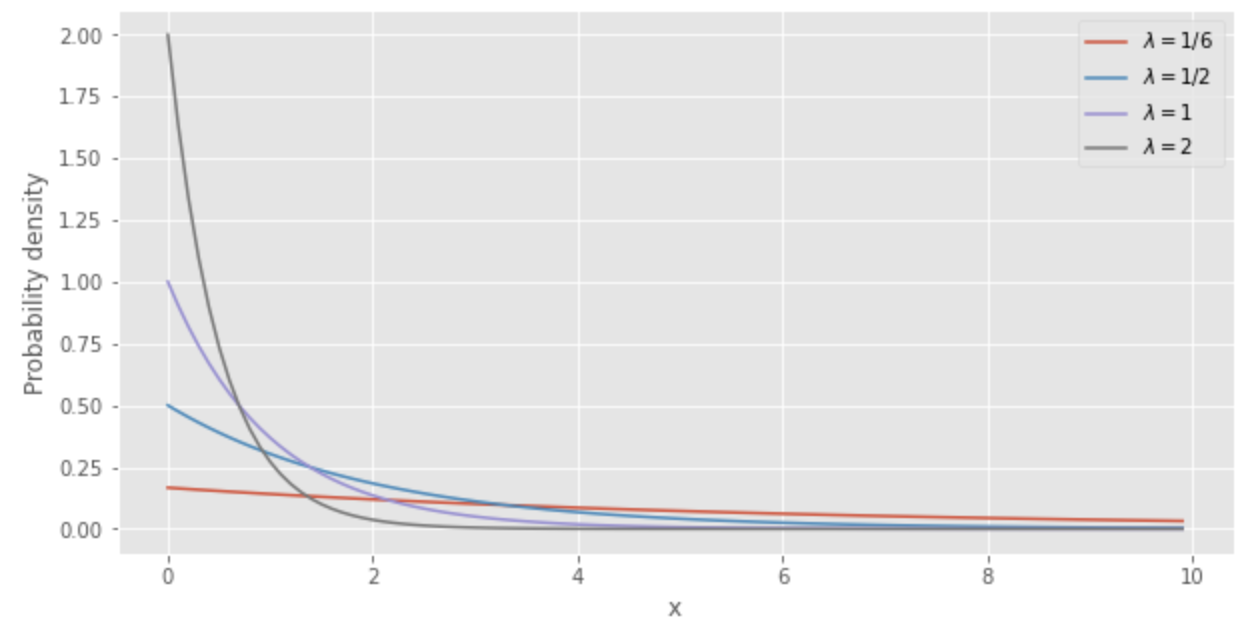
The smaller the value of \lambda, the slower the decrease, and the more monotonically decreasing it always is, independent of the value of \lambda.

Expected value and variance of exponential distribution

The expected value and variance of the exponential distribution are respectively:

Memoryless of exponential distribution

If the random variable X follows an exponential distribution and m, n > 0, then the following equation holds

The above equation implies that the time until the occurrence of a future event is independent of the existence of that past event. This property is called memoryless. Exponential distribution is the only continuous distribution with the memoryless.

Relationship to Poisson distribution

The exponential distribution is a probability distribution that follows the time it takes for an event to occur, while the Poisson distribution is a probability distribution that follows the number of times an event occurs in a unit of time. In other words, the exponential distribution considers the same event in terms of time, while the Poisson distribution considers it in terms of number of times.

Python Code

The following Python code can be used to plot the exponential distribution.

from scipy.stats import expon
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

plt.style.use('ggplot')
plt.figure(figsize=(10,5))

x = np.arange(0, 10, 0.1)
y_1_6 = expon.pdf(x=x, scale=6)
y_1_2 = expon.pdf(x=x, scale=2)
y_1 = expon.pdf(x=x, scale=1)
y_2 = expon.pdf(x=x, scale=1/2)
plt.plot(x, y_1_6, label='$\lambda=1/6$')
plt.plot(x, y_1_2, label='$\lambda=1/2$')
plt.plot(x, y_1, label='$\lambda=1$')
plt.plot(x, y_2, label='$\lambda=2$')
plt.legend()
plt.xlabel("x")
plt.ylabel("Probability density")