2022-12-09

Dirichlet distribution

What is Dirichlet distribution

The Dirichlet distribution is the distribution that the probability $x_i$ of each event occurring when $K$ events each occur $\alpha_{i}-1$ times. Note that $\alpha _{i}$ need not be an integer.

The probability density function of the Dirichlet distribution is expressed by the following equation:

f(x_1, x_2,.., x_{K-1}) = \frac{\Gamma(\sum^K_{i=1} \alpha_i)}{\prod_{i=1}^K\Gamma(\alpha_i)}\prod_{i=1}^Kx_i^{\alpha_i-1}

\sum^n_{i=1} = 1, \quad x_i \in \{0, 1 \}

In the above equation, the case $K=2$ corresponds to the probability density function of beta distribution. In other words, Dirichlet distribution is a multivariate extension of beta distribution.

Expected value and variance of Dirichlet distribution

The expected value and variance of the Dirichlet distribution are respectively as follows.

E(X_i)=\frac{\alpha_i}{\sum^{K}_{i=1}\alpha_i} \quad (i=1,2,...,K-1)

V(X_i)=\frac{\alpha_i(\sum^{K}_{i=1} \alpha_i-\alpha_i)}{(\sum^{K}_{i=1}\alpha_i)^2 (\sum^{K}_{i=1}\alpha_i + 1)} \quad (i=1,2,...,K-1)

Check the effect of parameters

Let us visualize a 3-dimensional ( $K=3$ ) Dirichlet distribution in Python.

import numpy as np
from scipy import special
from scipy.stats import dirichlet
import matplotlib
import matplotlib.pyplot as plt

plt.style.use('ggplot')

class Dirichlet():
    def __init__(self, param: list) -> None:
        self.param = np.array(param)

    def pdf(self, x: list) -> np.float:
        x_ar = np.array(x)
        cons = np.prod(special.gamma(self.param))/(special.gamma(np.sum(self.param)))
        p = (1./cons) * np.prod(x_ar**(self.param-1))
        return p

    def plt_3d(self, nrow: int, ncol: int, n: int, zlim=None)->None:
        xdata = np.linspace(0, 1, 200)
        ydata = np.linspace(0, 1, 200)
        X,Y = np.meshgrid(xdata, ydata)
        z = []
        X[X+Y>1] = 0
        Y[X+Y>1] = 0
        for _x, _y, _z in zip(X.flatten(), Y.flatten(), (1-X-Y).flatten()):
            z.append(self.pdf([_x, _y, _z]))

        Z = np.array(z).reshape(X.shape)
        fig = plt.figure(figsize=(10, 3))
        ax = plt.axes(projection='3d')
        ax.plot_surface(X, Y, Z, cmap='plasma')
        ax.set_zlim(zlim)
        ax.set_xlabel("$x_1$")
        ax.set_ylabel("$x_2$")
        ax.set_zlabel("PDF")
        ax.set_title("Dir($\\vec{\\alpha} = $" + "%s)" % self.param)
        plt.show()

Dirichlet([1.,1.,1.]).plt_3d(2, 2, 1, zlim=(0, 2.1))
Dirichlet([5.,5.,5.]).plt_3d(2, 2, 2)
Dirichlet([5.,1.,1.]).plt_3d(2, 2, 3)
Dirichlet([1.,5.,1.]).plt_3d(2, 2, 2)

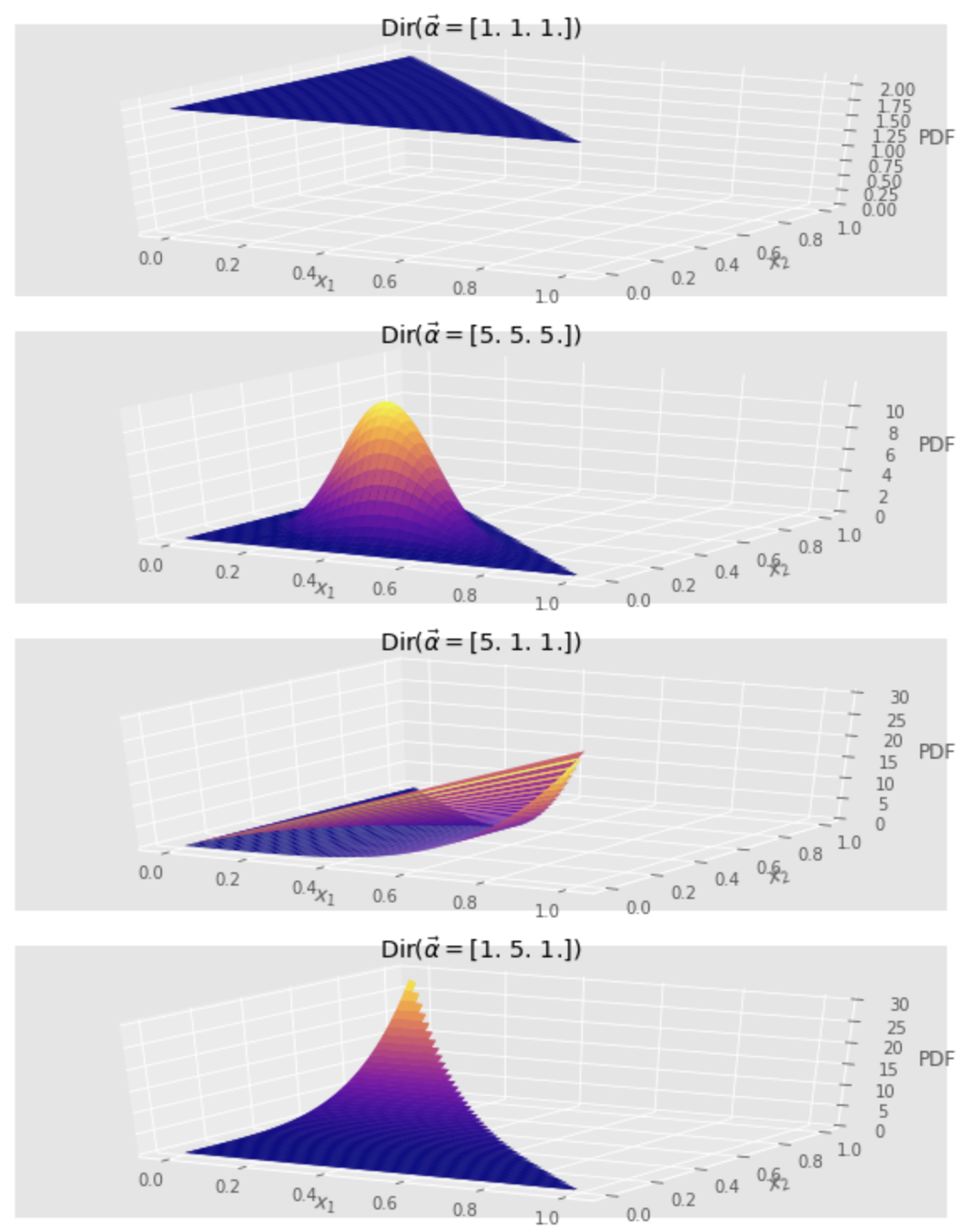
Dirichlet distribution

When the three $\alpha$ have the same value, we can see that the larger the $\alpha$ is, the smaller the variance is. Also, we can see that random variables with larger $\alpha$ have higher probability densities.

Dirichlet distribution

What is Dirichlet distribution

Expected value and variance of Dirichlet distribution

Check the effect of parameters

Exponential distribution

t-distribution

Ryusei Kakujo