Apa itu Traveling Salesman Problem (TSP)

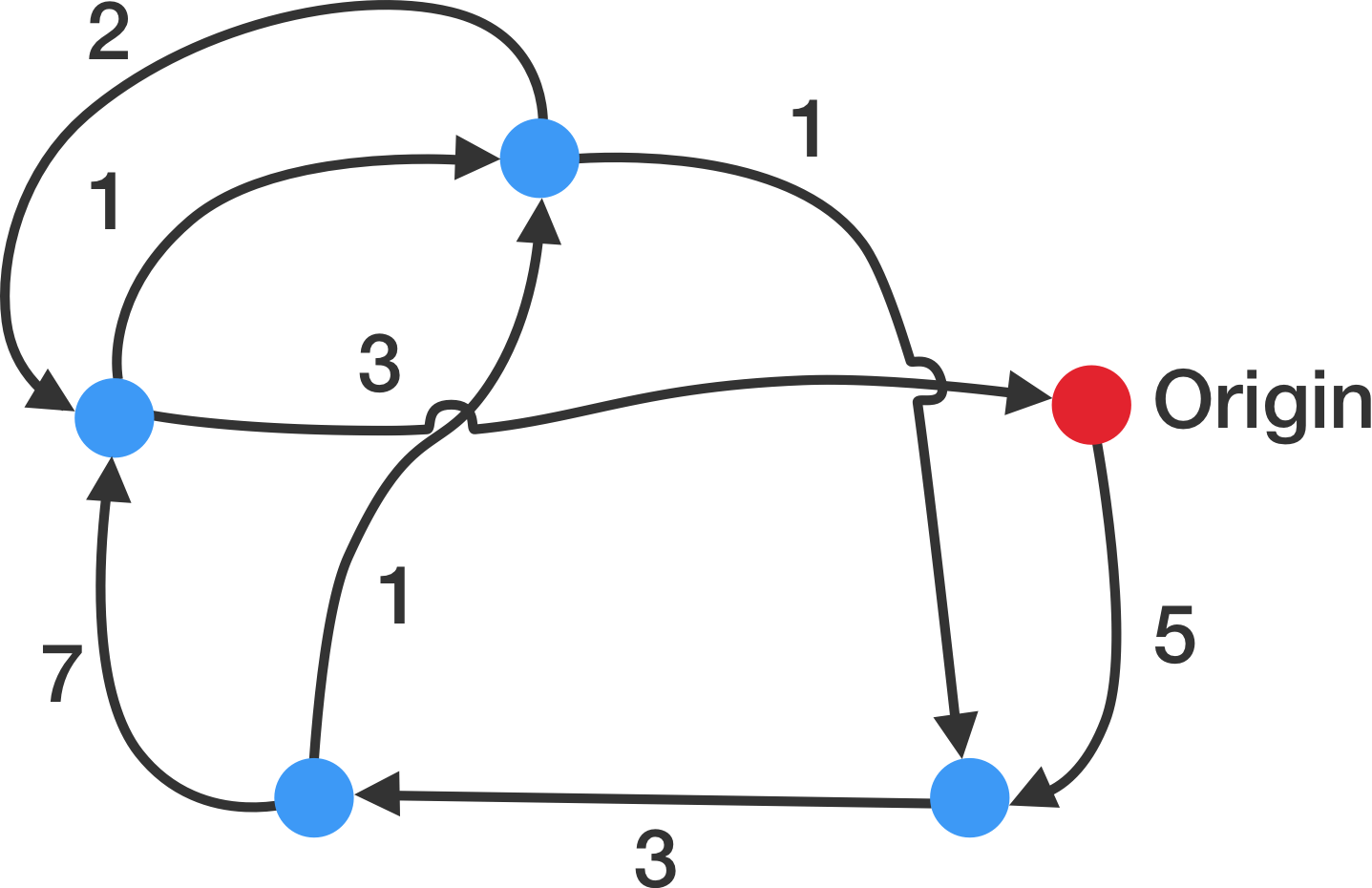
Traveling Salesman Problem (TSP) adalah masalah algoritma klasik dalam bidang ilmu komputer dan penelitian operasi yang berfokus pada optimasi. Dalam bentuk paling sederhananya, TSP berkaitan dengan seorang salesman yang perlu melakukan perjalanan ke sejumlah kota, dengan tantangan untuk menemukan rute terpendek yang memungkinkan salesman mengunjungi setiap kota hanya sekali dan kembali ke kota asal.

Masalah ini mudah dipahami namun cukup kompleks untuk dipecahkan, terutama ketika jumlah kota (atau 'simpul') meningkat. Dalam istilah matematika, ini adalah masalah dalam optimasi kombinatorial, karena melibatkan pencarian solusi terbaik dari himpunan solusi yang terbatas.

Traveling Salesperson Problem

Kompleksitas Masalah

Dalam ilmu komputer, kompleksitas suatu algoritma adalah ukuran jumlah resource komputasi, seperti waktu dan ruang, yang diperlukan oleh algoritma untuk memecahkan suatu masalah. Kompleksitas TSP secara langsung terkait dengan jumlah kota yang harus dikunjungi oleh salesman.

Ketika mengevaluasi kompleksitas TSP, kita harus mempertimbangkan kompleksitas waktu, yaitu waktu pemrosesan komputasi yang diperlukan untuk memecahkan masalah, dan kompleksitas ruang, yaitu jumlah ruang memori yang dibutuhkan.

Misalnya, pendekatan dengan brute force, di mana semua rute yang mungkin dihitung dan dibandingkan, akan memiliki kompleksitas waktu faktorial, ditulis sebagai O(n!). Ini berarti bahwa waktu yang diperlukan untuk memecahkan masalah tumbuh secara eksponensial dengan jumlah kota, sehingga pendekatan ini tidak praktis untuk masalah yang lebih besar.

P vs NP

Dalam bidang teori komputasi, masalah sering diklasifikasikan ke dalam kategori-kategori untuk mencerminkan tingkat kesulitannya. Di antara kategori-kategori tersebut adalah P (masalah yang dapat diselesaikan dengan cepat) dan NP (masalah yang solusinya dapat diperiksa dengan cepat). Pertanyaan apakah P sama dengan NP adalah salah satu masalah yang paling fundamental dan belum terpecahkan dalam ilmu komputer.

TSP diklasifikasikan sebagai masalah NP-Hard. Ini berarti bahwa setidaknya seberat masalah-masalah terberat dalam NP. Jika dapat ditemukan algoritma yang dapat menyelesaikan TSP dengan cepat (dalam "waktu polinomial"), maka algoritma tersebut dapat digunakan untuk menyelesaikan semua masalah lain dalam NP, dengan demikian membuktikan bahwa P = NP. Namun, meskipun penelitian yang ekstensif, belum ditemukan algoritma seperti itu, dan banyak ilmuwan komputer menduga bahwa algoritma semacam itu tidak ada.

Variasi TSP

TSP Simetris

Dalam TSP simetris, jarak dari kota A ke kota B sama dengan jarak dari kota B ke kota A. Ini adalah bentuk paling umum dari masalah ini dan yang paling banyak dikenal oleh banyak orang. Banyak skenario dunia nyata, seperti jaringan jalan, dapat diwakili sebagai TSP simetris.

TSP Asimetris

Dalam TSP asimetris, jarak dari kota A ke kota B tidak selalu sama dengan jarak dari kota B ke kota A. Variasi ini berlaku dalam skenario di mana rute perjalanan tidak saling bolak-balik, seperti perjalanan dengan pesawat di mana penerbangan langsung tidak tersedia antara setiap pasang bandara, atau dalam skenario logistik di mana terlibat jenis jalan yang berbeda dan jalan satu arah.

Variasi Lainnya

Terdapat banyak variasi lain dari TSP, masing-masing dengan fitur dan tantangan unik. Beberapa di antaranya adalah:

• Multiple TSP (mTSP)
  Pada variasi ini, lebih dari satu salesman tersedia, dan tujuannya adalah meminimalkan total jarak yang ditempuh oleh semua salesmen.

• Time-dependent TSP
  Di sini, waktu perjalanan antara kota-kota bergantung pada waktu keberangkatan. Variasi ini sering digunakan dalam skenario di mana kemacetan lalu lintas bervariasi pada waktu-waktu yang berbeda dalam sehari.

• Vehicle routing problem (VRP)
  Ini adalah bentuk umum dari TSP di mana sebuah armada kendaraan harus dirutekan secara optimal.

Pendekatan Solusi

Dalam mengatasi Traveling Salesman Problem, terdapat dua kelas algoritma yang umum digunakan: algoritma eksak dan algoritma heuristik.

Algoritma eksak dirancang untuk memberikan solusi yang tepat dan optimal untuk masalah tersebut. Metode ini menjamin menemukan rute terpendek yang mungkin. Namun, karena kompleksitas komputasional TSP yang tinggi, algoritma eksak cenderung mahal secara komputasi dan praktis hanya untuk masalah dengan ukuran kecil.

Algoritma heuristik, di sisi lain, dirancang untuk efisiensi daripada akurasi. Metode ini memberikan solusi pendekatan dan sangat berharga saat menangani masalah skala besar di mana solusi yang tepat mungkin tidak mungkin karena keterbatasan waktu dan resource komputasi. Meskipun heuristik tidak menjamin rute terpendek, seringkali mereka memberikan solusi yang cukup baik yang 'cukup dekat' dengan solusi optimal.

Algoritma Eksak

Pencarian Brute-Force

Solusi paling dasar untuk TSP adalah pencarian brute-force. Algoritma ini menghitung biaya dari semua tur yang mungkin, lalu memilih yang paling murah. Meskipun pendekatan ini menjamin solusi optimal, pendekatan ini menjadi tidak praktis secara komputasi ketika jumlah kota meningkat karena kompleksitas faktorialnya.

Algoritma Held-Karp

Algoritma Held-Karp adalah solusi pemrograman dinamik yang secara signifikan mengurangi kompleksitas waktu yang dibutuhkan untuk memecahkan TSP dibandingkan dengan pendekatan brute-force. Algoritma ini menghitung jalur terpendek yang mengunjungi setiap kota dengan membangun solusi secara bertahap, dengan memanfaatkan hasil perhitungan sebelumnya untuk menghindari perhitungan yang redundan. Meskipun begitu, algoritma ini tetap memiliki kompleksitas waktu eksponensial, sehingga penggunaannya terbatas pada masalah dengan ukuran yang relatif kecil.

Algoritma Heuristik

Algoritma Nearest Neighbor

Algoritma Nearest Neighbor adalah heuristik sederhana di mana salesman selalu pergi ke kota terdekat yang belum dikunjungi. Metode ini tidak menjamin solusi optimal, tetapi cepat dan sering kali cukup baik untuk keperluan praktis.

Simulated Annealing

Simulated Annealing adalah teknik probabilitas yang menjelajahi ruang solusi dengan menerima solusi yang kurang optimal pada tahap awal pencarian, membantu menghindari titik minimum lokal. Seiring berjalannya waktu, eksplorasi secara bertahap menjadi lebih terfokus, meniru proses pendinginan annealing dalam metalurgi.

Algoritma Genetika

Algoritma genetika adalah jenis heuristik yang terinspirasi dari proses seleksi alam. Solusi untuk TSP dianggap sebagai individu dalam populasi, dan dari generasi ke generasi, populasi berevolusi menuju solusi yang lebih baik melalui operasi mutasi, persilangan (rekombinasi), dan seleksi. Pendekatan ini dapat diparalelkan dengan baik dan dapat memberikan solusi berkualitas tinggi untuk masalah yang besar, meskipun tidak menjamin solusi optimal.

Kemajuan Terkini dalam Solusi TSP

Komputasi Kuantum

Komputasi kuantum, dengan potensi komputasi paralelnya, membuka frontier baru dalam upaya untuk memecahkan masalah yang sulit seperti TSP yang termasuk dalam kelas NP-hard. Komputer kuantum dapat menjelajahi beberapa solusi secara bersamaan, memanfaatkan konsep yang dikenal sebagai superposisi. Pendekatan ini berpotensi mengurangi secara drastis waktu yang dibutuhkan untuk memecahkan TSP, terutama untuk ukuran masalah yang lebih besar.

Saat ini, bidang komputasi kuantum masih dalam tahap awal, dan pengembangan algoritma kuantum untuk memecahkan TSP merupakan area penelitian yang aktif. Hasil awal menunjukkan potensi yang menjanjikan, menunjukkan bahwa seiring dengan matangnya teknologi, kita mungkin dapat memecahkan masalah TSP dengan ukuran yang lebih besar secara lebih efisien daripada dengan komputer klasik.

Pendekatan Pembelajaran Mesin

Pembelajaran mesin adalah bidang lain yang telah digunakan dalam pemecahan TSP. Dengan melatih model pada sejumlah contoh masalah TSP, algoritma pembelajaran mesin dapat belajar untuk memperkirakan solusi TSP.

Salah satu pendekatan yang terkenal adalah menggunakan pembelajaran penguatan (reinforcement learning), di mana agen belajar cara memecahkan TSP dengan mengambil tindakan dalam suatu lingkungan dan menerima umpan balik dalam bentuk reward. Tujuan agen adalah belajar kebijakan yang memaksimalkan total reward, yang dalam kasus TSP, berarti meminimalkan total jarak tur.

Pendekatan lain menggunakan jaringan saraf (neural networks) untuk mempelajari sebuah heuristik dalam memecahkan TSP. "Heuristik saraf" ini dilatih pada dataset contoh masalah dan solusinya, belajar untuk memprediksi kota berikutnya yang akan dikunjungi dalam tur berdasarkan kondisi saat ini dari masalah.

Meskipun pendekatan pembelajaran mesin ini tidak menjamin solusi optimal, mereka dapat memberikan solusi berkualitas tinggi dalam sebagian kecil waktu yang dibutuhkan oleh algoritma eksak, menjadikannya jalur yang menjanjikan untuk memecahkan instansi TSP yang lebih besar.