Apa itu Teori Kompleksitas Komputasional

Teori kompleksitas komputasional adalah cabang ilmu komputer yang mempelajari resource komputasi yang diperlukan untuk menyelesaikan suatu masalah komputasi tertentu. Resource ini meliputi waktu (berapa langkah yang diperlukan untuk menyelesaikan masalah) dan ruang (berapa banyak memori yang dibutuhkan untuk menyelesaikan masalah), tetapi ukuran kompleksitas lainnya juga dapat dipertimbangkan.

Tujuan utama dari teori kompleksitas komputasional adalah mengklasifikasikan masalah berdasarkan tingkat kesulitannya yang melekat pada masalah tersebut. Untuk melakukannya, teori ini mendefinisikan kelas-kelas kompleksitas - himpunan masalah yang dapat diselesaikan menggunakan jumlah resource komputasi yang serupa. Kelas-kelas kompleksitas yang penting termasuk P, NP, dan banyak lainnya.

Aspek sentral dari teori kompleksitas komputasional adalah studi tentang masalah-masalah yang sulit, yaitu masalah-masalah yang tidak memiliki solusi efisien yang diketahui. Melalui eksplorasi masalah-masalah ini dan masalah lainnya, teori kompleksitas komputasional memberikan wawasan penting tentang batasan apa yang dapat dan tidak dapat dilakukan oleh komputer, membimbing desain algoritma, pengembangan perangkat lunak, dan kemajuan teknologi komputasi secara keseluruhan.

Kompleksitas Waktu

Kompleksitas waktu adalah konsep dalam teori kompleksitas komputasional yang mewakili waktu komputasi yang dibutuhkan oleh suatu algoritma dalam menjalankan fungsinya, sebagai fungsi dari ukuran masukan program. Ini adalah salah satu faktor kritis dalam menentukan efisiensi suatu algoritma.

Notasi Big-O

Notasi Big-O adalah notasi matematika yang digunakan untuk menjelaskan batas atas, atau skenario kasus terburuk, dari kompleksitas waktu suatu algoritma. Ini menggambarkan bagaimana waktu eksekusi suatu algoritma tumbuh seiring dengan ukuran masukan. Misalnya, algoritma dengan kompleksitas waktu O(n) akan mengalami peningkatan waktu eksekusi secara linier dengan ukuran masukan.

O(1): Kompleksitas Waktu Konstan

Suatu algoritma dikatakan memiliki kompleksitas waktu konstan ketika tidak bergantung pada ukuran masukan. Tidak peduli seberapa besar masukan Anda, waktu komputasi akan tetap konstan.

Contoh

Mengakses elemen tertentu dalam sebuah array. Tidak peduli seberapa besar array tersebut, hanya butuh satu langkah untuk membaca elemen array jika indeksnya diketahui.

O(n): Kompleksitas Waktu Linier

Suatu algoritma dikatakan memiliki kompleksitas waktu linier ketika waktu eksekusi meningkat paling banyak secara linier dengan ukuran data masukan.

Contoh

Fungsi pencarian sederhana yang iterasi melalui sebuah array untuk mencari nilai tertentu akan memiliki kompleksitas waktu O(n), karena dalam kasus terburuk, algoritma perlu melihat setiap elemen sekali.

O(log n): Kompleksitas Waktu Logaritmik

Kompleksitas waktu logaritmik terkait dengan algoritma yang membagi ukuran masalah menjadi fraksi dengan setiap langkah.

Contoh

Pencarian biner adalah algoritma dengan kompleksitas waktu logaritmik, O(\log n). Setiap langkah dari algoritma pencarian biner membagi jumlah elemen yang perlu dicari menjadi setengahnya, sehingga diperlukan langkah-logaritmik lebih sedikit untuk menemukan target.

O(n^2): Kompleksitas Waktu Kuadratik

Suatu algoritma dikatakan memiliki kompleksitas waktu kuadratik ketika perlu melakukan proses untuk setiap elemen, dan proses tersebut melibatkan pengulangan elemen lain.

Contoh

Bubble sort adalah contoh klasik dari algoritma dengan kompleksitas O(n^2). Untuk setiap elemen dalam array, bubble sort membandingkannya dengan setiap elemen lainnya.

O(2^n): Kompleksitas Waktu Eksponensial

Kompleksitas waktu eksponensial terjadi ketika pertumbuhan ganda dengan setiap penambahan ke set data masukan. Kurva pertumbuhan fungsi O(2^n) adalah eksponensial - mulai sangat landai, kemudian naik dengan cepat.

Contoh

Contoh klasik dari kompleksitas O(2^n) adalah perhitungan rekursif bilangan Fibonacci. Algoritma rekursif naif melakukan komputasi yang berlebihan yang terduplikasi, efektifnya melipatgandakan jumlah pekerjaan untuk setiap peningkatan ukuran masukan.

Kompleksitas Ruang

Kompleksitas ruang adalah konsep penting lainnya dalam teori kompleksitas komputasional. Ini mewakili jumlah ruang memori yang dibutuhkan oleh suatu algoritma dalam hubungannya dengan ukuran masukan. Seperti halnya kompleksitas waktu, pemahaman tentang kompleksitas ruang suatu algoritma penting dalam menilai efisiensinya, terutama dalam lingkungan dengan batasan memori.

Kelas-Kelas Kompleksitas

Kelas-kelas kompleksitas adalah cara untuk mengelompokkan masalah komputasi yang memiliki karakteristik berbasis resource yang serupa. Karakteristik ini sering terkait dengan waktu atau ruang yang diperlukan untuk menyelesaikan masalah.

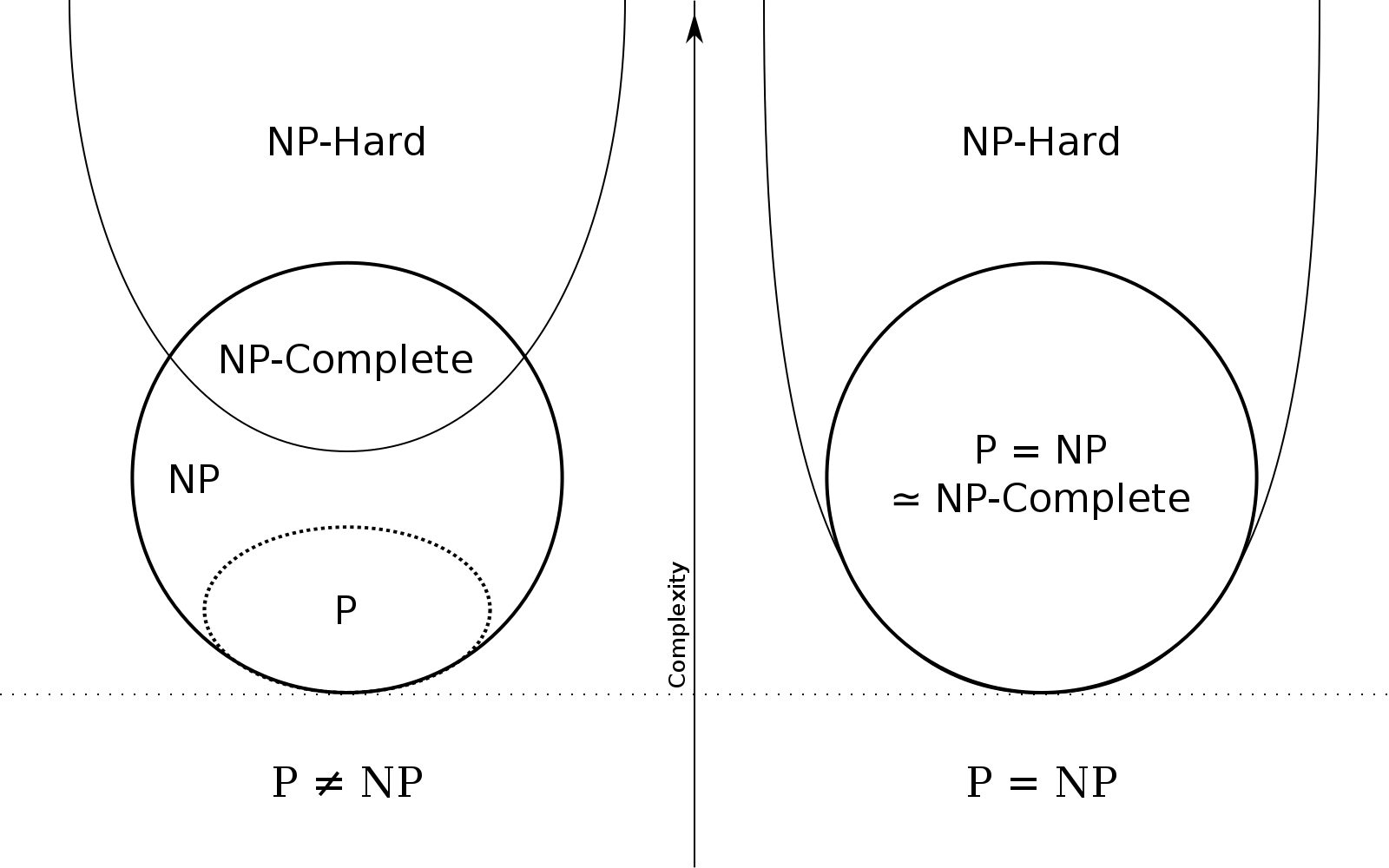
File:P np np-complete np-hard.svg

Kelas P

Kelas P (Waktu Polinomial) terdiri dari masalah keputusan yang dapat dipecahkan oleh mesin Turing deterministik dalam waktu polinomial. Dalam notasi Big O, ini berarti ada beberapa polinomial p(n) sehingga kompleksitas waktu dalam menyelesaikan masalah adalah O(p(n)).

Sebagai contoh, masalah yang dapat diselesaikan dalam waktu O(n^2), di mana n adalah ukuran masukan, berada dalam P. Ini berarti bahwa seiring dengan pertumbuhan masukan, waktu yang diperlukan untuk menyelesaikan masalah tersebut tumbuh secara kuadrat.

Kelas NP

Kelas NP berisi masalah yang, begitu solusinya diberikan, dapat diverifikasi dalam waktu polinomial oleh mesin Turing deterministik. Ini tidak sama dengan mengatakan bahwa masalah tersebut dapat diselesaikan dalam waktu polinomial. Lebih tepatnya, ini berarti bahwa jika seseorang memberikan Anda solusi potensial, Anda dapat memeriksa kebenarannya dalam waktu polinomial.

Sebagai contoh, jika Anda memiliki solusi potensial untuk sebuah masalah dan Anda dapat memverifikasi kebenarannya dalam waktu O(n^3), maka masalah tersebut berada dalam NP.

Masalah NP-Complete

NP-Complete merupakan kumpulan masalah yang mana setiap masalah dalam NP dapat direduksi ke dalam waktu polinomial.

Kelas NP-Complete memiliki dua sifat utama:

• Masalah itu sendiri berada dalam NP. Ini berarti bahwa jika kita diberikan 'sertifikat', atau solusi potensial untuk masalah tersebut, kita dapat memverifikasi kebenaran solusi ini dalam waktu polinomial.
• Setiap masalah dalam NP dapat direduksi ke dalam waktu polinomial ke dalam masalah tersebut. Dengan kata lain, solusi dengan waktu polinomial untuk masalah ini akan memungkinkan kita menyelesaikan semua masalah dalam NP dalam waktu polinomial pula.

Masalah NP-Hard

NP-Hard adalah kelas masalah yang secara informal mewakili masalah "terberat" dalam NP (Nondeterministic Polynomial time), meskipun tidak selalu berada dalam NP itu sendiri.

Sebuah masalah dikatakan NP-Hard jika setiap masalah dalam NP dapat direduksi ke masalah tersebut dalam waktu polinomial. Ini berarti jika Anda dapat menyelesaikan masalah NP-Hard dalam waktu polinomial, Anda juga dapat menyelesaikan semua masalah dalam NP dalam waktu polinomial.

Penting untuk dicatat bahwa meskipun semua masalah NP-Complete adalah NP-Hard, tidak semua masalah NP-Hard adalah NP-Complete. Perbedaan di sini adalah bahwa masalah NP-Hard tidak perlu berada dalam NP itu sendiri, dan tidak perlu memiliki solusi yang dapat diverifikasi dalam waktu polinomial.

Masalah P versus NP

Masalah "P versus NP" adalah pertanyaan mendasar dalam teori kompleksitas komputasional. Ini mempertanyakan apakah P (masalah yang dapat diselesaikan dalam waktu polinomial) sama dengan NP (masalah yang solusinya dapat diverifikasi dalam waktu polinomial).

Signifikansi P versus NP

Masalah P versus NP bukan hanya pertanyaan teoretis; jawabannya memiliki implikasi praktis yang signifikan. Jika ternyata P = NP, itu berarti setiap masalah yang dapat kita verifikasi solusinya dengan cepat juga dapat kita selesaikan dengan cepat. Hal ini akan merevolusi bidang seperti kriptografi, optimisasi, teori database, kecerdasan buatan, dan banyak lagi.

Di sisi lain, jika P ≠ NP, itu berarti ada masalah yang tidak dapat diselesaikan dengan algoritma cepat (dalam asumsi bahwa solusi harus benar untuk semua input). Hal ini akan mengonfirmasi keamanan dari banyak algoritma enkripsi, karena ketidakmungkinan menyelesaikan beberapa masalah menjadi dasar kriptografi modern.

Status Masalah P versus NP

Meskipun upaya dari banyak pemikir brilian, masalah P versus NP tetap belum terpecahkan dan dianggap sebagai salah satu masalah terbesar yang belum terpecahkan dalam ilmu komputer. Sebenarnya, masalah ini termasuk dalam tujuh "Masalah Hadiah Milenium" di mana Institut Matematika Clay menawarkan hadiah $1 juta untuk solusi yang benar.

Percaya umum di kalangan ilmu komputer adalah bahwa kemungkinan P tidak sama dengan NP (P ≠ NP), terutama karena kurangnya algoritma efisien untuk masalah NP-complete. Namun, belum ada yang dapat membuktikan hal ini dengan tegas.