Skewness distribusi probabilitas

Skewness dari distribusi probabilitas adalah indikator kemiringan (derajat asimetri) dari distribusi. Skewness dari distribusi tergantung pada nilai seperti di bawah ini:

• skewness <0
  Distribusi miring ke kanan.
• skewness = 0
  Distribusi simetris.
• skewness > 0
  Distribusi miring ke kiri.

Gambar di bawah ini menunjukkan distribusi normal standar dengan skewness yang bervariasi dari distribusi normal.

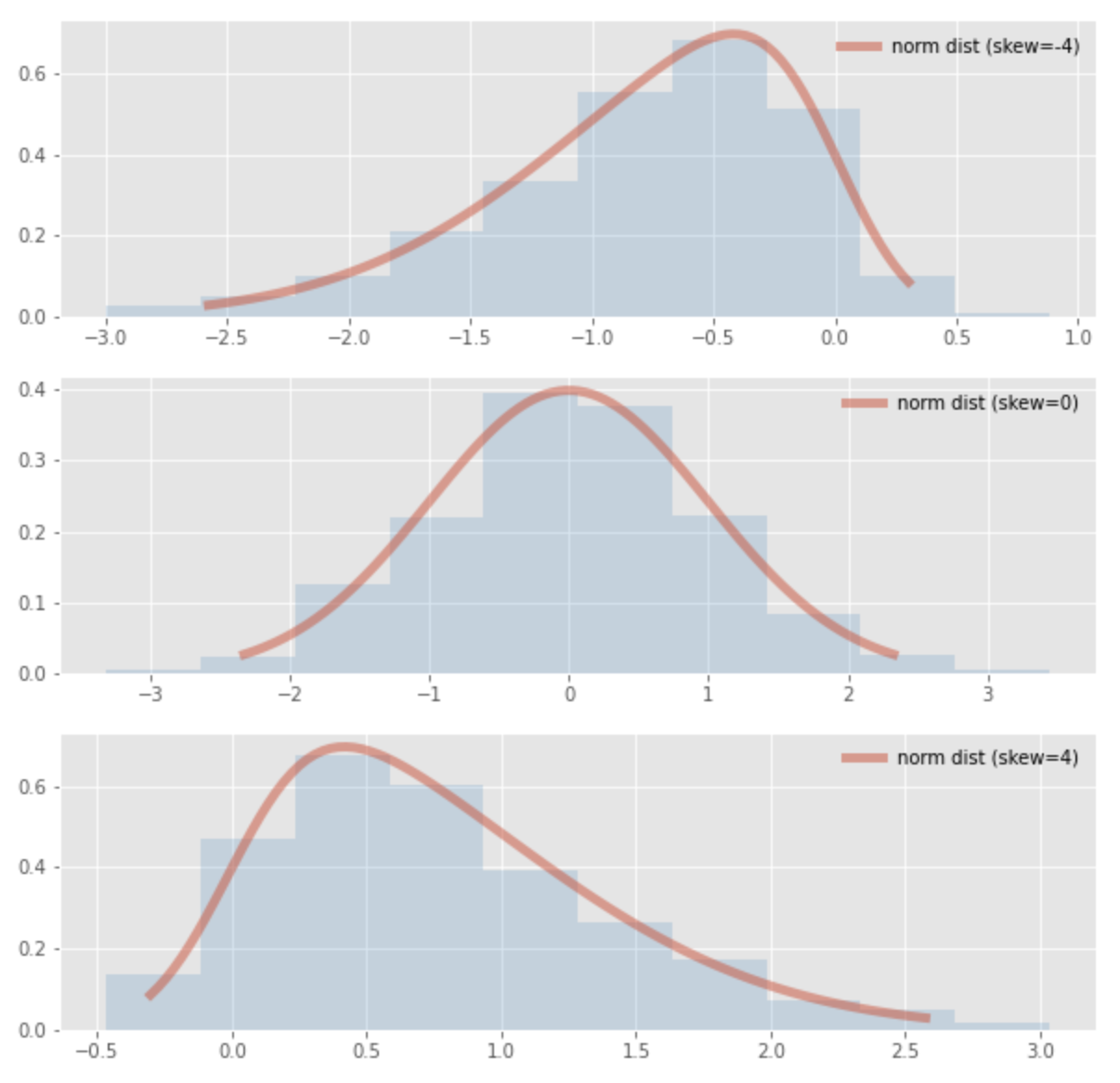
Dalam kasus distribusi normal, skewness dapat diperoleh dengan rumus berikut:

Kurtosis dari distribusi probabilitas

Kurtosis dari distribusi probabilitas adalah ukuran tingkat ketajaman atau penyebaran distribusi sehubungan dengan distribusi normal. Sebuah distribusi yang lebih tajam dari distribusi normal akan memiliki nilai kurtosis positif, sedangkan distribusi yang lebih lambat dari distribusi normal akan memiliki nilai kurtosis negatif.

Gambar di bawah ini menunjukkan distribusi Laplace dengan kurtosis 2,228, distribusi normal dengan kurtosis 0,045, dan distribusi uniform dengan kurtosis -1,161.

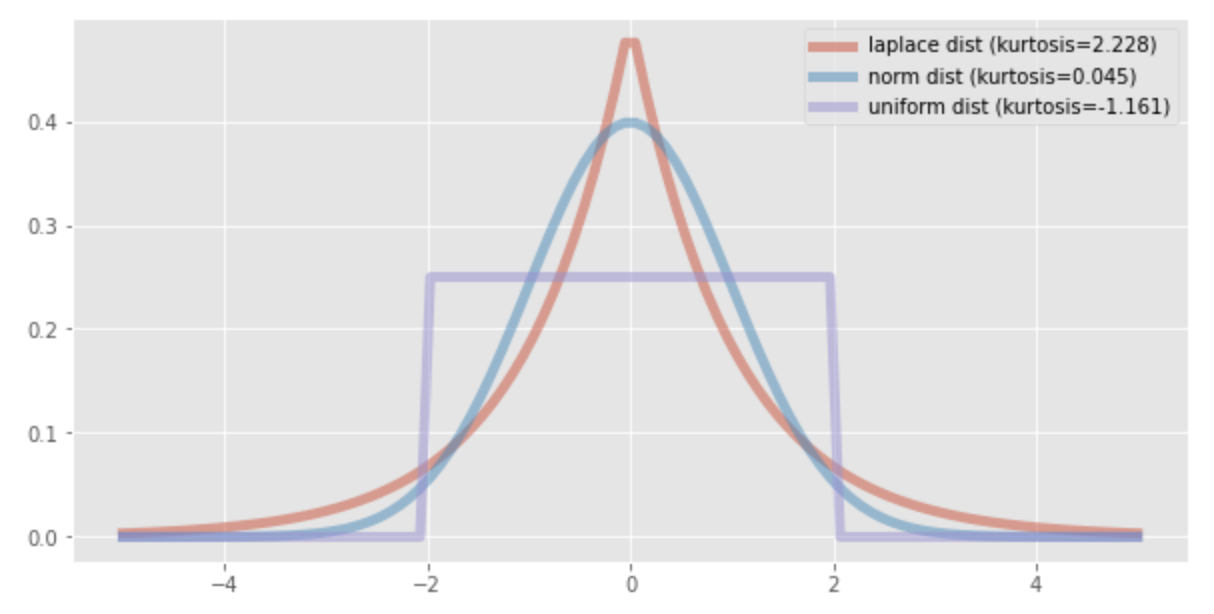
Untuk distribusi normal, kurtosis dapat diperoleh dengan menggunakan rumus berikut:

Kode Python

Kode Python untuk menggambar skewness dan kurtosis dari distribusi probabilitas ini ditunjukkan di bawah ini.

from scipy.stats import skewnorm
import matplotlib.pyplot as plt
import numpy as np

plt.style.use('ggplot')
fig, ax = plt.subplots(facecolor="w", figsize=(10, 10))

skews = [-4, 0, 4]

for i, skew in enumerate(skews):
    plt.subplot(3, 1, i+1)
    x = np.linspace(skewnorm.ppf(0.01, skew),
                    skewnorm.ppf(0.99, skew), 100)
    plt.plot(x, skewnorm.pdf(x, skew), lw=5, alpha=0.5, label=f'norm dist (skew={skew})')
    r = skewnorm.rvs(skew, size=1000)
    plt.hist(r, density=True, histtype='stepfilled', alpha=0.2)
    plt.legend(loc='best', frameon=False)
plt.show()

import matplotlib.pyplot as plt
import scipy.stats as stats
from scipy.stats import kurtosis

plt.style.use('ggplot')
fig, ax = plt.subplots(facecolor="w", figsize=(10, 5))

x = np.linspace(-5, 5, 100)
ax = plt.subplot()
distnames = ['laplace', 'norm', 'uniform']

for distname in distnames:
    if distname == 'uniform':
        dist = getattr(stats, distname)(loc=-2, scale=4)
    else:
        dist = getattr(stats, distname)
    data = dist.rvs(size=1000)
    kur = kurtosis(data, fisher=True)
    y = dist.pdf(x)
    ax.plot(x, y, lw=5, alpha=0.5, label="{} dist (kurtosis={})".format(distname, round(kur, 3)))
    ax.legend()

Referensi

https://www.kaggle.com/code/sandhyakrishnan02/normal-distribution-skewness-and-kurtosis/notebook#Kurtosis
https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.skewnorm.html
https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.kurtosis.html