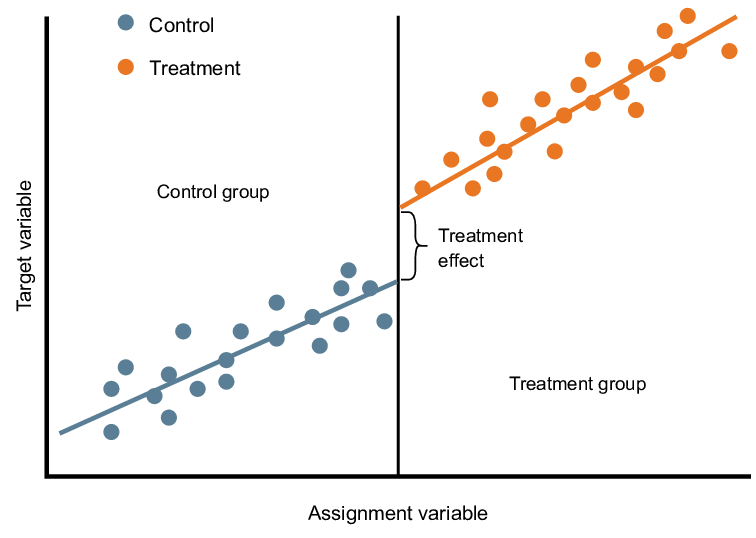
Regression Discontinuity Design (RDD)

Regression Discontinuity Design (RDD) adalah metode penelitian yang memungkinkan kita untuk mengestimasi efek kausal dari intervensi atau perlakuan ketika penugasan acak ke kelompok-kelompok tidak mungkin dilakukan karena pertimbangan etis, praktis, atau pertimbangan lainnya. RDD membuat ini menjadi mungkin dengan memanfaatkan bentuk khusus dari penugasan non-acak—perlakuan atau intervensi ditugaskan berdasarkan aturan ambang atau batas pada variabel penugasan yang bersifat kontinu dan dapat diukur.

Ide dasarnya cukup sederhana: jika skor individu pada variabel penugasan (juga dikenal sebagai variabel pendorong) di atas atau di bawah titik ambang tertentu, individu tersebut ditugaskan ke kelompok perlakuan atau kelompok kontrol tertentu. Hal ini bisa semudah menentukan siapa yang memenuhi syarat untuk mendapatkan beasiswa berdasarkan IPK atau memutuskan sekolah mana yang menerima dana tambahan berdasarkan status sosial ekonomi masyarakat.

Yang membuat RDD khususnya kuat adalah kemampuannya untuk mengestimasi efek kausal dari intervensi dalam pengaturan quasi-eksperimental. Artinya, meskipun penugasan ke perlakuan tidak acak, desain RDD dapat meniru karakteristik dari eksperimen acak, setidaknya secara lokal di sekitar ambang batas. Hal ini dimungkinkan karena unit-unit yang sedikit di atas dan di bawah ambang batas cenderung sangat mirip satu sama lain, kecuali untuk status perlakuan. Oleh karena itu, setiap loncatan diskontinu dalam hasil pada ambang batas dapat diatribusikan kepada efek kausal dari perlakuan.

An illustration explaining the Regression Discontinuity Design model, and how the average treatment effect is estimated.

Asumsi RDD

Validitas RDD sangat bergantung pada beberapa asumsi kunci yang harus dipenuhi. Pelanggaran terhadap asumsi-asumsi ini berpotensi mengarah pada estimasi yang bias terhadap efek kausal.

Kontinuitas

Asumsi paling kritis dalam RDD adalah kontinuitas hasil potensial dalam ketiadaan perlakuan pada ambang batas. Ini berarti bahwa dalam ketiadaan perlakuan, hubungan fungsional antara variabel penugasan dan hasilnya halus pada titik ambang batas. Tidak boleh ada lonjakan dalam hubungan ini pada ambang batas selain yang disebabkan oleh perlakuan. Asumsi ini diperlukan karena menjadi dasar perbandingan lokal dalam RDD yang mengestimasi efek perlakuan.

Lokalitas

Asumsi kedua, lokalitas, didasarkan pada prinsip prinsip randomisasi lokal atau kesamaan lokal. Asumsi ini mengasumsikan bahwa unit-unit yang dekat dengan ambang batas lebih mirip satu sama lain daripada dengan unit-unit yang lebih jauh. Pada dasarnya, ini menciptakan sebuah "eksperimen mini" di sekitar ambang batas, di mana unit-unit yang sedikit di bawah dan di atas ambang batas berfungsi sebagai kelompok kontrol dan perlakuan masing-masing. Jika asumsi ini terpenuhi, setiap perbedaan dalam hasil rata-rata antara kelompok-kelompok ini dapat diatribusikan kepada efek perlakuan.

Tidak Dapat Dimanipulasi

Asumsi ini memastikan bahwa individu atau unit tidak dapat secara tepat memanipulasi variabel penugasan untuk memastikan perlakuan. Dengan kata lain, harus ada tingkat keacakkan di sekitar ambang batas untuk mencegah unit-unit memastikan status perlakuan mereka. Jika kondisi ini dilanggar, dapat memperkenalkan bias sistematis ke dalam estimasi efek perlakuan karena unit-unit yang sedikit di atas dan di bawah ambang batas mungkin secara fundamental berbeda satu sama lain.

Irrelevansi

Asumsi terakhir, irrelevansi, mengasumsikan bahwa ambang batas tidak relevan untuk hasil potensial kecuali melalui pengaruhnya terhadap penugasan perlakuan. Ini berarti bahwa ambang batas tidak secara langsung memengaruhi hasil potensial selain melalui perlakuan. Jika asumsi ini tidak terpenuhi, diskontinuitas pada ambang batas dapat disebabkan oleh alasan selain perlakuan, yang mengarah pada estimasi yang bias terhadap efek perlakuan.

Derivasi Efek Kausal oleh RDD

Salah satu daya tarik utama dari RDD adalah kemampuannya untuk mengestimasi efek kausal dalam pengaturan di mana penugasan perlakuan tidak acak tetapi didasarkan pada aturan ambang batas.

Mengestimasi Efek Kausal

RDD mengestimasi efek kausal dari perlakuan dengan memanfaatkan diskontinuitas pada ambang batas variabel penugasan. Ide dasarnya adalah bahwa unit-unit yang sedikit di bawah dan di atas ambang batas hampir identik, kecuali untuk status perlakuan yang melompat pada ambang batas. Oleh karena itu, efek kausal dari perlakuan dapat diestimasi sebagai lonjakan dalam hasil rata-rata pada ambang batas.

Secara matematis, kita dapat menunjukkan hasil potensial dari unit i ketika status perlakuan adalah w sebagai Y_i(w). Hasil yang diamati Y_i kemudian diberikan oleh:

Y_i = W_iY_i(1) + (1 - W_i)Y_i(0)

Di sini, W_i adalah status perlakuan aktual dari unit i, yang bernilai 1 jika variabel penugasan X_i di atas ambang batas c, dan 0 jika tidak.

Local average treatment effect (LATE) di ambang batas kemudian diestimasi sebagai perbedaan batas dari hasil yang diharapkan sedikit di atas dan di bawah ambang batas:

LATE = E[Y_i(1) - Y_i(0) | X_i = c] = E[Y_i | X_i = c^+] - E[Y_i | X_i = c^-]

Di sini, c^+ dan c^- menunjukkan batas dari kanan (di atas ambang batas) dan batas dari kiri (di bawah ambang batas) secara berturut-turut.

Metode dan Strategi

Ada berbagai strategi dan metode untuk mengestimasi LATE dalam RDD. Biasanya melibatkan penerapan model regresi terpisah untuk kelompok perlakuan dan kontrol, dan kemudian membandingkan hasil yang diprediksi pada ambang batas.

Metode Parametrik

Metode parametrik menggunakan model regresi parametrik untuk data terpisah di setiap sisi ambang batas. Model regresi linear sederhana dapat diformulasikan sebagai berikut:

Y_i = a + bX_i + cW_i + d(X_i - c)W_i + e_i

Here, (X_i - c)W_i is an interaction term that allows for different slopes on either side of the cutoff, and e_i is a random error term.

The causal effect of the treatment at the cutoff is estimated by the coefficient c, which captures the jump in the regression line at the cutoff.

Metode Non-parametrik

Metode non-parametrik, di sisi lain, tidak memaksa bentuk fungsional pada hubungan antara variabel penugasan dan hasil. Sebaliknya, mereka menggunakan regresi polinomial lokal atau regresi kernel untuk mengestimasi hasil yang diharapkan sedikit di atas dan di bawah ambang batas.

Contoh RDD

Untuk mengilustrasikan penerapan RDD dalam praktik, kita akan mempertimbangkan studi kasus hipotetis tentang program pendidikan yang bertujuan untuk meningkatkan kinerja akademik siswa.

Latar Belakang

Misalkan sebuah distrik sekolah di Amerika Serikat telah menerapkan program beasiswa untuk membantu siswa yang mengalami kesulitan meningkatkan kinerja akademik mereka. Program ini menyediakan resource akademik tambahan, seperti bimbingan belajar gratis dan materi pendidikan, kepada siswa yang memiliki nilai rata-rata (GPA) di bawah ambang batas tertentu. Dalam kasus ini, ambang batas GPA ditetapkan pada 2,5. Setiap siswa dengan GPA di bawah ambang batas ini memenuhi syarat untuk program tersebut.

Sebagai peneliti pendidikan, Anda tertarik untuk mengestimasi efek kausal dari program ini terhadap kinerja akademik siswa, yang diukur melalui perubahan GPA dari satu tahun akademik ke tahun berikutnya.

Implementasi RDD

Dengan mengingat sifat implementasi program ini—di mana terdapat batasan yang jelas untuk kelayakan program—RDD menjadi metode yang sesuai untuk mengestimasi efeknya. Variabel pendorong dalam konteks ini adalah GPA siswa, dan variabel perlakuan adalah apakah siswa menerima manfaat program beasiswa atau tidak.

Pertama, Anda akan mengumpulkan data tentang GPA siswa yang sedikit di atas dan di bawah ambang batas, bersama dengan data tentang perubahan GPA mereka untuk tahun akademik berikutnya.

Selanjutnya, dengan menggunakan analisis grafis, Anda dapat memeriksa secara visual apakah terdapat diskontinuitas atau "lonjakan" dalam perubahan rata-rata GPA pada titik ambang batas 2,5 GPA.

Lebih lanjut, untuk mengestimasi efek perlakuan secara formal, Anda dapat menggunakan model regresi. Jika Anda mengasumsikan hubungan linear antara GPA dan perubahan GPA, Anda dapat menggunakan model regresi linear sederhana. Jika hubungan tersebut lebih kompleks, Anda mungkin menggunakan metode non-parametrik seperti regresi polinomial lokal.

Melalui langkah-langkah ini, Anda dapat mengestimasi efek kausal dari program beasiswa terhadap kinerja akademik siswa, yaitu seberapa banyak program tersebut meningkatkan GPA siswa secara rata-rata.

Analisis

Berdasarkan hasil analisis Anda, Anda dapat menyimpulkan tentang efektivitas program beasiswa tersebut. Jika program memiliki efek positif, Anda akan mengamati lonjakan positif yang signifikan dalam perubahan GPA pada titik ambang batas.