Apa itu Distribusi Gumbel

Distribusi Gumbel adalah jenis distribusi nilai ekstrim yang memodelkan perilaku nilai maksimum (atau minimum) dari kumpulan variabel acak independen dan identik terdistribusi. Distribusi ini sangat berguna untuk menganalisis peristiwa ekstrem, seperti bencana alam, krisis keuangan, atau kegagalan teknik. Distribusi ini ditandai dengan dua parameter: parameter lokasi (\mu) dan parameter skala (\sigma), yang menentukan kecenderungan pusat dan dispersi, masing-masing.

Dasar Matematika Distribusi Gumbel

Fungsi Densitas Probabilitas (PDF)

Untuk variabel acak kontinu, fungsi densitas probabilitas (PDF) memberikan nilai probabilitas. Untuk distribusi Gumbel, PDF diberikan oleh:

di mana \mu adalah parameter lokasi dan \sigma adalah parameter skala. PDF membantu menjelaskan bentuk dan perilaku distribusi Gumbel dan dapat digunakan untuk memperkirakan probabilitas dan nilai yang diharapkan.

Fungsi Distribusi Kumulatif (CDF)

Fungsi distribusi kumulatif (CDF) mewakili probabilitas bahwa variabel acak mengambil nilai kurang dari atau sama dengan nilai yang diberikan. Untuk distribusi Gumbel, CDF diberikan oleh:

CDF memberikan wawasan tentang perilaku ekor distribusi dan dapat digunakan untuk menghitung persentil dan statistik ringkasan lainnya.

Momen dan Fungsi Karakteristik

Momen memberikan informasi penting tentang bentuk dan kecenderungan pusat distribusi. Momen ke-n distribusi Gumbel dapat diungkapkan menggunakan fungsi gamma, \Gamma:

di mana \zeta adalah fungsi zeta Riemann. Momen pertama (n=1) sesuai dengan nilai yang diharapkan atau rata-rata, dan momen sentral kedua (n=2) sesuai dengan varians.

Fungsi karakteristik adalah cara lain untuk menjelaskan distribusi dan didefinisikan sebagai transformasi Fourier dari PDF. Fungsi karakteristik distribusi Gumbel diberikan oleh:

di mana \gamma adalah konstanta Euler-Mascheroni, dan t adalah variabel kompleks.

Estimasi Parameter: Lokasi dan Skala

Mengestimasi parameter lokasi (\mu) dan skala (\sigma) dari distribusi Gumbel sangat penting untuk memasangkan model ke data yang diamati. Dua teknik estimasi umum adalah:

• Estimasi Maksimum Kemungkinan (MLE)
  Metode ini memaksimalkan fungsi kemungkinan dari data yang diamati, diberikan parameter distribusi. Ini memberikan estimasi yang tidak bias dan efisien secara asimtotik untuk parameter lokasi dan skala.

• Metode Momen
  Pendekatan ini mencocokkan momen sampel (rata-rata dan varians) dengan momen teoretis dari distribusi Gumbel. Ini memberikan estimasi yang konsisten, meskipun kurang efisien dibandingkan dengan MLE.

Aplikasi Distribusi Gumbel

Artikel ini menjelajahi beberapa aplikasi penting dari Distribusi Gumbel, termasuk hidrologi, rekayasa, keuangan, dan pembelajaran mesin.

Analisis Nilai Ekstrim dalam Hidrologi

Ahli hidrologi sering mengandalkan Distribusi Gumbel untuk menganalisis peristiwa ekstrem seperti banjir dan kekeringan. Ini membantu mereka memperkirakan probabilitas kejadian dan besarnya peristiwa tersebut, memberikan wawasan berharga untuk merancang infrastruktur seperti bendungan, jembatan, dan tanggul. Dengan memahami distribusi curah hujan atau debit sungai yang ekstrem, ahli hidrologi dapat membuat keputusan yang berinformasi untuk meningkatkan pengelolaan resource air dan meningkatkan strategi mitigasi banjir.

Penilaian Risiko dalam Rekayasa

Dalam bidang rekayasa, Distribusi Gumbel memainkan peran kritis dalam penilaian dan pengelolaan risiko. Insinyur menggunakan distribusi ini untuk menganalisis probabilitas kegagalan struktur dalam beban ekstrem atau kondisi lingkungan yang ekstrem. Dengan menentukan tegangan atau beban maksimum yang dapat ditahan oleh suatu struktur, mereka dapat merancang dan memelihara infrastruktur yang lebih aman dan lebih andal. Aplikasi ini sangat relevan dalam rekayasa sipil, struktural, dan lingkungan.

Optimasi Portofolio dalam Keuangan

Distribusi Gumbel adalah alat yang berharga dalam keuangan untuk mengoptimalkan portofolio investasi. Manajer portofolio sering menggunakannya untuk memodelkan pengembalian ekstrem aset keuangan, memungkinkan mereka memperkirakan kerugian potensial selama peristiwa pasar yang ekstrem. Dengan memasukkan Distribusi Gumbel dalam model Value-at-Risk (VaR) dan analisis risiko ekor, investor dapat membuat keputusan yang lebih terinformasi untuk meminimalkan kerugian potensial dan meningkatkan pengembalian yang disesuaikan dengan risiko.

Pembelajaran Mesin dan Jaringan Saraf

Dalam beberapa tahun terakhir, Distribusi Gumbel telah ditemukan dalam domain pembelajaran mesin dan jaringan saraf buatan. Salah satu contoh yang menonjol adalah teknik Gumbel-Softmax, yang digunakan untuk pengambilan sampel diskrit dalam pembelajaran penguatan dan masalah optimasi. Teknik Gumbel-Softmax memanfaatkan Distribusi Gumbel untuk mendekati distribusi probabilitas diskrit, memungkinkan proses pelatihan yang lebih efisien dan stabil. Selain itu, peneliti sedang mengeksplorasi potensi Distribusi Gumbel dalam algoritme pembelajaran mendalam untuk memodelkan peristiwa ekstrem, seperti titik data langka atau anomali, yang dapat meningkatkan deteksi anomali dan meningkatkan kekokohan model.

Kode Python

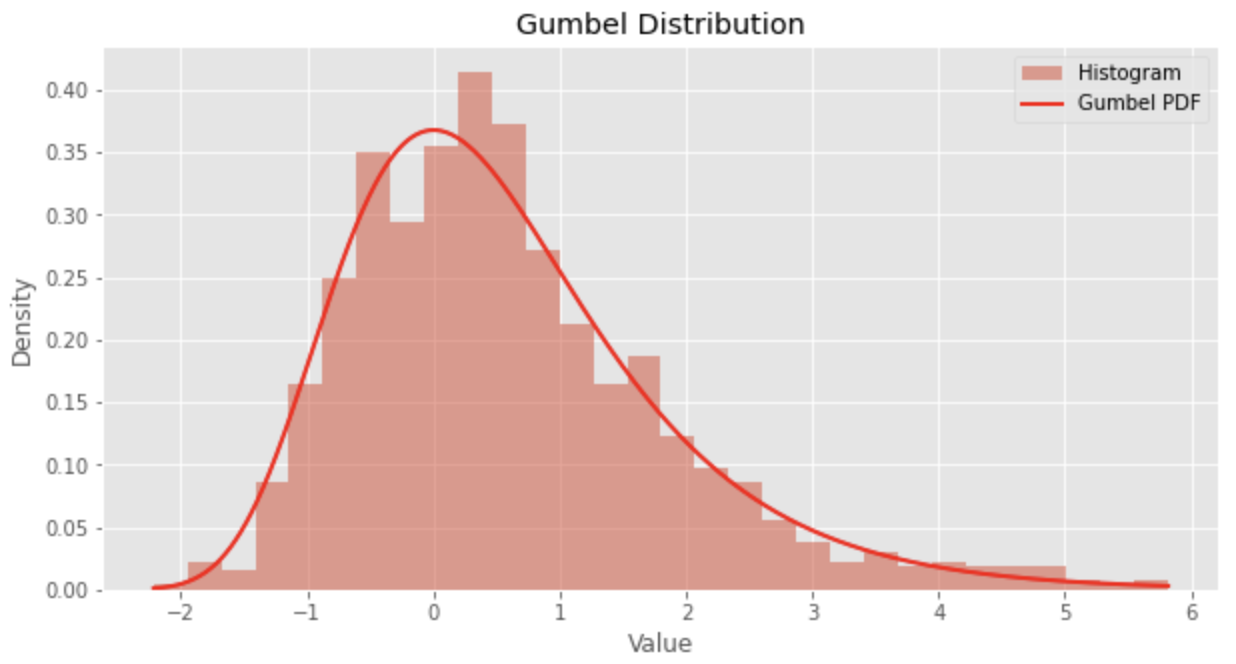
Berikut adalah contoh kode untuk menggambar distribusi Gumbel dengan Python.

Python Code

Here is a sample code for drawing a Gumbel distribution with Python.

import numpy as np
import matplotlib.pyplot as plt

plt.style.use('ggplot')
fig, ax = plt.subplots(facecolor="w", figsize=(10, 5))

# Gumbel distribution parameters
mu = 0      # Location parameter
sigma = 1    # Scale parameter
size = 1000 # Number of data points

# Generate Gumbel distributed data points
gumbel_data = np.random.gumbel(mu, sigma, size)

# Plot the histogram
plt.hist(gumbel_data, bins=30, density=True, alpha=0.5, label='Histogram')

# Calculate the Gumbel PDF
x = np.linspace(np.min(gumbel_data), np.max(gumbel_data), 1000)
pdf = (1/sigma) * np.exp(-(x-mu)/sigma - np.exp(-(x-mu)/sigma))

# Plot the Gumbel PDF
plt.plot(x, pdf, 'r-', lw=2, label='Gumbel PDF')

# Configure the plot
plt.title('Gumbel Distribution')
plt.xlabel('Value')
plt.ylabel('Density')
plt.legend()

# Show the plot
plt.show()