2022-10-01

Clustering

Apa itu Clustering

Clustering adalah teknik fundamental dalam ilmu data yang membantu mengungkap pola dan struktur tersembunyi dalam data. Ini merupakan bentuk pembelajaran tanpa pengawasan, yang berarti bahwa algoritma mencoba mengidentifikasi struktur dasar data tanpa pengetahuan sebelumnya tentang label atau kategori data. Clustering mengelompokkan data yang mirip berdasarkan fitur mereka, menciptakan klaster yang menunjukkan tingkat homogenitas tertentu. Klaster ini kemudian dapat digunakan untuk memahami hubungan yang mendasari dalam data dan menghasilkan wawasan yang berharga.

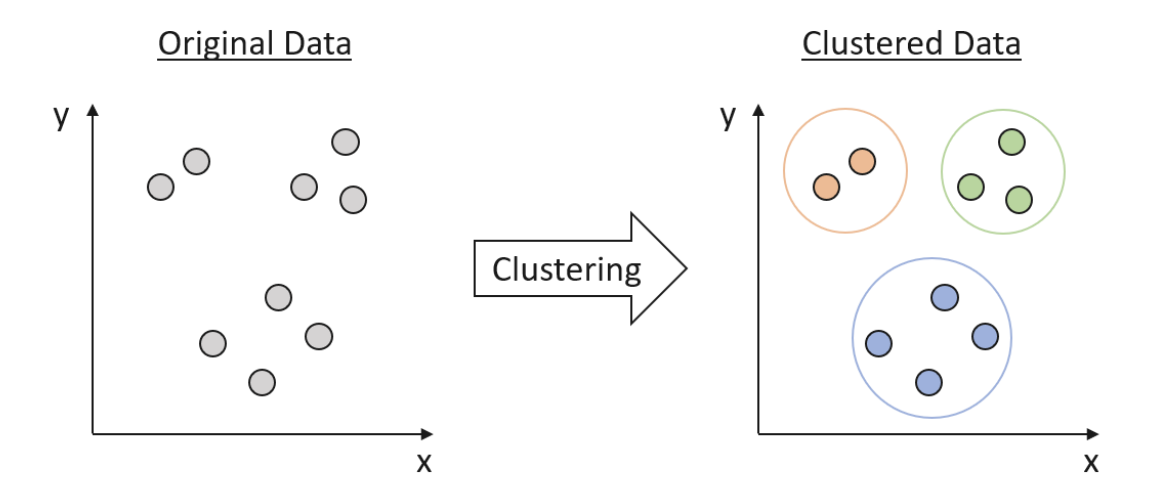
Clustering basics and a demonstration in clustering infrastructure pathways

Metrik Jarak

Konsep fundamental dalam clustering adalah pengukuran kesamaan atau perbedaan antara data. Metrik jarak mengukur perbedaan antara data, dengan jarak yang lebih kecil menunjukkan kesamaan yang lebih besar. Beberapa metrik jarak yang umum digunakan antara lain:

Jarak Euclidean
Metrik jarak yang paling banyak digunakan, menghitung jarak garis lurus antara dua titik di ruang Euclidean.
Jarak Manhattan
Juga dikenal sebagai jarak L1, menghitung jumlah perbedaan absolut antara koordinat dua titik.
Kesamaan Kosinus
Mengukur kosinus sudut antara dua vektor, menunjukkan kesamaan mereka. Ini sangat berguna ketika menangani data berdimensi tinggi atau data teks yang direpresentasikan sebagai vektor frekuensi istilah.
Jarak Mahalanobis
Memperhitungkan korelasi antara fitur dan invariant terhadap skala, sehingga berguna ketika menangani data yang berkorelasi atau tidak homogen.
Kesamaan Jaccard
Mengukur kesamaan antara dua set dengan membagi ukuran persimpangan mereka dengan ukuran gabungan mereka. Ini sering digunakan untuk data biner atau kategorikal.

Validitas dan Evaluasi Klaster

Mengevaluasi kualitas hasil clustering penting dalam menentukan efektivitas algoritma dan parameter yang dipilih. Indeks validitas klaster menyediakan pengukuran kuantitatif untuk menilai kualitas hasil clustering. Indeks-indeks ini dapat dibagi menjadi tiga kategori:

Indeks internal
Menilai hasil clustering berdasarkan properti intrinsik dari data, seperti jarak dalam klaster dan antar-klaster. Contoh termasuk indeks Silhouette, indeks Davies-Bouldin, dan indeks Calinski-Harabasz.
Indeks eksternal
Membandingkan hasil clustering dengan kebenaran dasar yang diketahui, yang biasanya diperoleh dari data yang diberi label. Contoh termasuk indeks Rand yang disesuaikan, indeks Fowlkes-Mallows, dan indeks Jaccard.
Indeks relatif
Membandingkan kinerja berbagai algoritma clustering atau pengaturan parameter pada dataset yang sama. Contoh termasuk statistik Gap, indeks C, dan indeks Dunn.

Algoritma Clustering

K-means Clustering

K-means adalah algoritma clustering berbasis partisi populer yang bertujuan untuk meminimalkan jumlah jarak kuadrat dalam klaster. Algoritma secara iteratif menetapkan titik data ke salah satu dari K klaster yang telah ditentukan berdasarkan kedekatan dengan pusat klaster, yang mewakili rata-rata dari semua titik data dalam klaster. Langkah utama dari algoritma K-means adalah:

Inisialisasi K pusat klaster secara acak.
Tetapkan setiap titik data ke pusat klaster terdekat.
Perbarui pusat klaster dengan menghitung rata-rata dari semua titik data di setiap klaster.
Ulangi langkah 2 dan 3 sampai konvergen (yaitu, pusat klaster tidak berubah lagi) atau mencapai jumlah iterasi yang telah ditentukan.

K-means sederhana, cepat, dan dapat diskalakan, sehingga cocok untuk dataset besar dan aplikasi real-time. Algoritma bekerja dengan baik ketika data menunjukkan struktur partisi yang jelas dengan klaster berbentuk isotropik dan cembung. Namun, K-means memiliki beberapa keterbatasan:

Membutuhkan pengguna untuk menentukan jumlah klaster (K) sebelumnya, yang mungkin tidak diketahui sebelumnya.
Algoritma sensitif terhadap penempatan awal pusat klaster dan mungkin konvergen ke nilai minimum lokal. Untuk mengurangi masalah ini, beberapa percobaan dengan inisialisasi yang berbeda dapat dilakukan, dan solusi terbaik dapat dipilih berdasarkan jumlah jarak kuadrat dalam klaster.
K-means sensitif terhadap outlier dan noise, yang dapat secara signifikan memengaruhi pusat klaster.
Algoritma mengasumsikan bahwa semua klaster memiliki ukuran, bentuk, dan kepadatan yang serupa, yang mungkin tidak benar untuk data dunia nyata.

Hierarchical Clustering

Algoritma hierarchical clustering membangun struktur berbentuk pohon (dendrogram) untuk mewakili hubungan tertanam antara titik data.

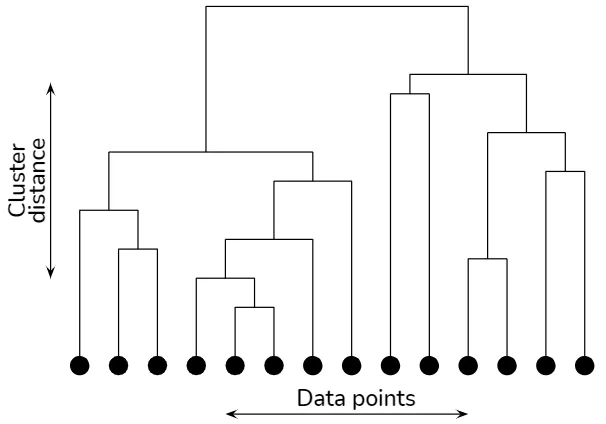
Dendrogram
Hierarchical clustering explained

Ada dua jenis utama hierarchical clustering:

Agglomerative (bottom-up)
Memulai dengan setiap titik data sebagai klaster terpisah dan secara iteratif menggabungkan pasangan klaster terdekat sampai hanya tersisa satu klaster.
Divisive (top-down)
Memulai dengan satu klaster yang berisi semua titik data dan secara rekursif membagi klaster menjadi klaster yang lebih kecil berdasarkan beberapa kriteria.

Pilihan metrik jarak dan kriteria penghubung, yang menentukan cara menghitung jarak antara klaster, berdampak signifikan pada dendrogram yang dihasilkan. Kriteria penghubung umum termasuk penghubung tunggal, penghubung lengkap, penghubung rata-rata, dan metode Ward.

DBSCAN (Density-Based Spatial Clustering of Applications with Noise)

DBSCAN adalah algoritma clustering berbasis densitas yang mengelompokkan titik data berdasarkan kedekatan dan kepadatan. Algoritma menentukan klaster sebagai daerah padat titik data yang terpisah oleh area kepadatan titik yang lebih rendah. DBSCAN membutuhkan dua parameter: radius lingkungan (eps) dan jumlah minimum titik yang diperlukan untuk membentuk daerah padat (minPts). Langkah utama dari algoritma DBSCAN adalah:

Untuk setiap titik data, tentukan tetangganya dalam radius eps.
Jika suatu titik data memiliki tetangga setidaknya sebanyak minPts, tandai sebagai titik inti; jika tidak, tandai sebagai titik noise.
Untuk setiap titik inti yang belum ditugaskan ke klaster, buat klaster baru dan tambahkan semua titik inti yang dapat dicapai secara langsung dan tidak langsung ke klaster.
Tugaskan titik noise ke klaster terdekat jika berada dalam radius eps dari titik inti; jika tidak, biarkan tidak ditugaskan.

DBSCAN tahan terhadap noise, karena dapat mengidentifikasi dan memisahkan titik noise dari klaster. Algoritma juga dapat mendeteksi klaster dengan bentuk arbitrer dan kepadatan yang bervariasi, tidak seperti K-means dan hierarchical clustering. Namun, DBSCAN membutuhkan pengguna untuk menentukan parameter eps dan minPts, yang dapat menantang. Pendekatan umum untuk memilih parameter ini adalah menggunakan grafik jarak k, di mana jarak ke tetangga ke-k diurutkan untuk setiap titik data secara terurut naik.

Gaussian Mixture Models

Gaussian Mixture Model (GMM) adalah model probabilistik generatif yang mewakili dataset sebagai campuran beberapa distribusi Gaussian. Algoritma Expectation-Maximization (EM) digunakan untuk memperkirakan parameter distribusi Gaussian dan proporsi pencampuran. Langkah utama dari algoritma EM adalah:

Inisialisasi parameter distribusi Gaussian dan proporsi pencampuran.
Langkah E: Hitung probabilitas posterior setiap titik data yang termasuk ke dalam setiap distribusi Gaussian, dengan mempertimbangkan perkiraan parameter saat ini.
Langkah M: Perbarui parameter distribusi Gaussian dan proporsi pencampuran berdasarkan probabilitas posterior.
Ulangi langkah 2 dan 3 sampai konvergen atau mencapai jumlah iterasi yang telah ditentukan.

GMM dapat memodelkan distribusi data yang kompleks dan secara otomatis memperkirakan struktur kovarian dari klaster. Namun, pengguna perlu menentukan jumlah distribusi Gaussian (komponen) sebelumnya. Teknik pemilihan model, seperti kriteria AIC dan Bayesian Information Criterion (BIC), dapat digunakan untuk memilih jumlah komponen optimal.

Spectral Clustering

Spectral clustering adalah teknik clustering berbasis grafik yang menggunakan properti spektral matriks Laplacian grafik untuk mengidentifikasi klaster dalam data. Algoritma dimulai dengan membangun grafik kesamaan, di mana setiap titik data adalah node, dan bobot sisi merepresentasikan kesamaan pairwise antara titik data. Matriks Laplacian grafik kemudian dihitung, dan vektor eigen-nya digunakan untuk melakukan reduksi dimensi dan clustering.

Spectral clustering khususnya efektif dalam mendeteksi klaster non-convex dan menangani data dengan struktur kompleks. Namun, algoritma ini dapat menjadi mahal secara komputasi untuk dataset yang besar karena dekomposisi eigen matriks Laplacian. Berbagai teknik pendekatan, seperti metode Nyström dan algoritma acak, dapat digunakan untuk meningkatkan skalabilitas spectral clustering.