2022-10-02

K-Means Clustering

Machine Learning

Clustering

Python

sklearn

Apa itu K-Means Clustering

K-Means Clustering adalah teknik machine learning tak terbimbing yang banyak digunakan untuk membagi dataset menjadi K klaster yang berbeda. Algoritma ini bertujuan untuk menetapkan setiap titik data ke suatu klaster sedemikian rupa sehingga meminimalkan variasi dalam klaster dan memaksimalkan variasi antar klaster. Secara esensial, algoritma ini berusaha untuk mengelompokkan titik data yang serupa berdasarkan nilai fitur mereka.

Algoritma K-Means

Fungsi Tujuan

Algoritma K-Means bertujuan untuk meminimalkan total sum of squares dalam klaster, juga dikenal sebagai fungsi tujuan atau cost function. Secara matematis, fungsi tujuan didefinisikan sebagai:

$J(C_1, C_2, \dots, C_K) = \sum_{i=1}^{K} \sum_{x \in C_i} ||x - \mu_i||^2$

Di sini, $K$ mewakili jumlah klaster, $C_i$ adalah klaster ke- $i$ , $x$ adalah titik data dalam klaster $C_i$ , dan $\mu_i$ adalah pusat (rata-rata) dari titik data dalam klaster $C_i$ . Tujuannya adalah untuk menemukan penugasan klaster dan pusat yang optimal yang meminimalkan fungsi tujuan.

Langkah-Langkah Algoritma K-Means

Algoritma K-Means terdiri dari langkah-langkah berikut:

Inisialisasi
Pilih $K$ pusat klaster awal secara acak dari titik data. Pusat-pusat ini dapat menjadi titik data aktual atau dihasilkan secara acak dalam rentang data.
Penugasan
Tentukan setiap titik data ke pusat klaster terdekat. Jarak antara titik data dan pusat klaster biasanya diukur menggunakan jarak Euclidean, tetapi metrik jarak lain juga dapat digunakan.
Pembaruan
Hitung pusat klaster baru dengan mengambil rata-rata dari semua titik data yang ditugaskan ke klaster tersebut.
Konvergensi
Ulangi langkah 2 dan 3 sampai posisi pusat klaster tidak berubah secara signifikan atau telah mencapai jumlah iterasi yang ditentukan sebelumnya.

Algoritma ini sensitif terhadap penempatan pusat awal klaster, dan inisialisasi yang berbeda dapat menghasilkan penugasan klaster akhir yang berbeda. Untuk mengatasi masalah ini, algoritma sering dijalankan beberapa kali dengan inisialisasi yang berbeda, dan hasil klaster akhir dipilih berdasarkan nilai fungsi tujuan terendah.

Memilih Jumlah Klaster yang Tepat (K)

Memilih jumlah klaster yang tepat (K) adalah hal yang penting untuk kinerja algoritma K-Means. Memilih nilai K yang kecil dapat menghasilkan underfitting, sementara nilai yang besar dapat menyebabkan overfitting. Pada bab ini, saya akan membahas tiga metode populer untuk menentukan nilai K yang optimal: Metode Elbow, Metode Silhouette, dan Statistik Gap.

Metode Elbow

Metode Elbow adalah teknik heuristik yang melibatkan plot variasi yang dijelaskan (inertia) sebagai fungsi dari jumlah klaster (K) dan mengidentifikasi titik "siku" pada plot. Inertia adalah jumlah jarak kuadrat antara setiap titik data dan pusat klaster yang ditugaskan. Saat K meningkat, inersia menurun, tetapi laju penurunannya menurun. Titik siku mewakili nilai K di mana laju penurunan inersia mulai melambat secara signifikan, mengindikasikan bahwa menambahkan lebih banyak klaster tidak memberikan perbaikan yang substansial.

Langkah-langkah untuk menerapkan Metode Elbow:

Jalankan algoritma K-Means dengan nilai K yang berbeda, biasanya berkisar dari 1 hingga nilai maksimum yang telah ditentukan sebelumnya.
Hitung inersia untuk setiap nilai K.
Plot inersia sebagai fungsi dari K.
Identifikasi titik siku pada plot, yang sesuai dengan nilai K yang optimal.

Metode Silhouette

Metode Silhouette mengukur kualitas pengelompokan dengan menghitung skor siluet untuk setiap titik data. Skor siluet, yang berkisar dari -1 hingga 1, adalah ukuran seberapa mirip titik data dengan klasternya sendiri dibandingkan dengan klaster lain.

Skor siluet yang tinggi menunjukkan bahwa titik data cocok dengan klasternya sendiri dan kurang cocok dengan klaster lain. Skor siluet rata-rata untuk semua titik data memberikan evaluasi keseluruhan dari kualitas pengelompokan.

Langkah-langkah untuk menerapkan Metode Silhouette:

Jalankan algoritma K-Means dengan nilai K yang berbeda, biasanya berkisar dari 2 hingga nilai maksimum yang telah ditentukan sebelumnya.
Hitung skor siluet untuk setiap titik data dan hitung skor siluet rata-rata untuk setiap nilai K.
Plot skor siluet rata-rata sebagai fungsi dari K.
Identifikasi nilai K yang memaksimalkan skor siluet rata-rata.

Statistik Gap

Gap Statistic adalah teknik lain yang digunakan untuk memperkirakan jumlah klaster yang optimal (K). Ia membandingkan variasi dalam klaster antara nilai K yang berbeda dengan nilai harapan dalam distribusi nol referensi.

Langkah-langkah untuk menerapkan Statistik Gap:

Jalankan algoritma K-Means dengan nilai K yang berbeda, biasanya berkisar dari 1 hingga nilai maksimum yang telah ditentukan sebelumnya.
Hitung total variasi dalam klaster (inersia) untuk setiap nilai K.
Buat dataset acak dengan dimensi dan rentang yang sama seperti dataset asli, untuk membuat distribusi nol referensi.
Jalankan algoritma K-Means pada dataset acak dan hitung total variasi dalam klaster (inersia) untuk setiap nilai K.
Hitung Statistik Gap untuk setiap K sebagai selisih antara logaritma inersia yang diamati dan logaritma inersia yang diharapkan dalam distribusi nol referensi.
Identifikasi nilai K yang memaksimalkan Statistik Gap.

Implementasi K-Means di Python

Kita akan menerapkan algoritma pengelompokan K-Means pada dataset Iris menggunakan Python dan memvisualisasikan hasil pengelompokan.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasets
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score

# Load Iris dataset
iris = datasets.load_iris()
data = iris.data
feature_names = iris.feature_names

# Create a DataFrame
df = pd.DataFrame(data, columns=feature_names)

# Elbow Method to determine the optimal number of clusters (K)
inertias = []
K_range = range(1, 11)

for K in K_range:
    kmeans = KMeans(n_clusters=K, random_state=42)
    kmeans.fit(df)
    inertias.append(kmeans.inertia_)

plt.figure(figsize=(8, 5))
plt.plot(K_range, inertias, marker='o', color='blue', alpha=0.5)
plt.xlabel("Number of Clusters (K)")
plt.ylabel("Inertia")
plt.title("Elbow Method for Optimal K")
plt.show()

# Silhouette Method to determine the optimal number of clusters (K)
silhouette_scores = []

for K in range(2, 11):
    kmeans = KMeans(n_clusters=K, random_state=42)
    kmeans.fit(df)
    silhouette_scores.append(silhouette_score(df, kmeans.labels_))

plt.figure(figsize=(8, 5))
plt.plot(range(2, 11), silhouette_scores, marker='o', color='blue', alpha=0.5)
plt.xlabel("Number of Clusters (K)")
plt.ylabel("Average Silhouette Score")
plt.title("Silhouette Method for Optimal K")
plt.show()

# Based on the visualizations, choose the optimal K value
optimal_K = 3

# Perform K-Means clustering with the optimal K value
kmeans = KMeans(n_clusters=optimal_K, random_state=42)
kmeans.fit(df)
labels = kmeans.labels_
df['Cluster'] = labels

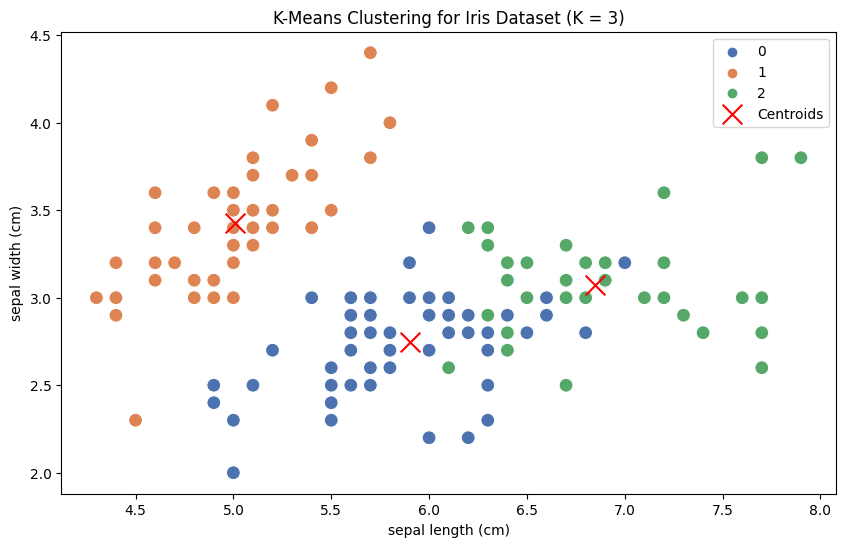
# Visualize the clustering result
plt.figure(figsize=(10, 6))
sns.scatterplot(x=df.iloc[:, 0], y=df.iloc[:, 1], hue=df['Cluster'], palette="deep", s=100)
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], c='red', marker='x', label='Centroids', s=200)
plt.xlabel(feature_names[0])
plt.ylabel(feature_names[1])
plt.title("K-Means Clustering for Iris Dataset (K = 3)")
plt.legend()
plt.show()

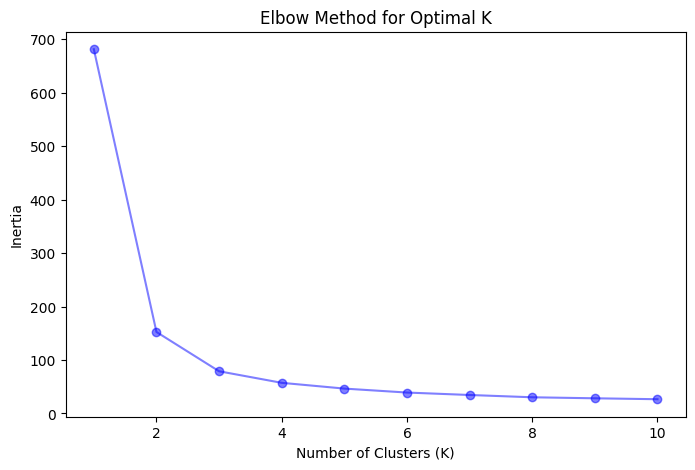
Elbow method
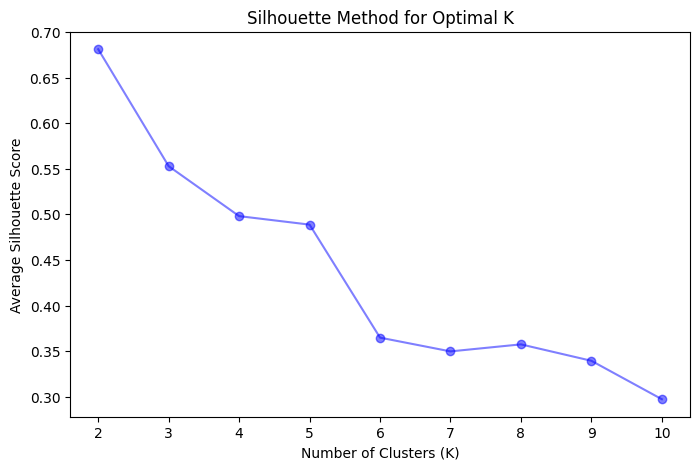
Silhouette method
K-Means method

Kode ini pertama memuat dataset Iris dan mengonversinya menjadi DataFrame. Kemudian, ia menggunakan Metode Elbow dan Metode Silhouette untuk memvisualisasikan jumlah klaster yang optimal (K). Berdasarkan visualisasi, kita memilih $K = 3$ sebagai nilai optimal.

Terakhir, kita melakukan pengelompokan K-Means dengan nilai K optimal dan memvisualisasikan hasil pengelompokan menggunakan plot titik-titik, di mana warna yang berbeda mewakili klaster yang berbeda, dan tanda 'x' merah mewakili pusat klaster masing-masing.