Apa itu distribusi chi-square

Distribusi chi-square adalah distribusi probabilitas yang diikuti oleh variabel acak X_1, X_2, \cdots, X_n ketika mereka independen satu sama lain dan masing-masing mengikuti distribusi normal standar N(0,1), di mana \chi^2 adalah

Fungsi densitas probabilitas dari distribusi chi-square dinyatakan dengan persamaan berikut:

Fungsi densitas probabilitas dari distribusi chi-square, seperti fungsi densitas probabilitas dari t-distribution, hanya memiliki parameter n. n disebut derajat kebebasan seperti pada distribusi-t. Distribusi chi-square kadang-kadang dilambangkan sebagai \chi^2(n).

Grafik dari distribusi chi-square tergantung pada derajat kebebasan n dan terlihat seperti ini.

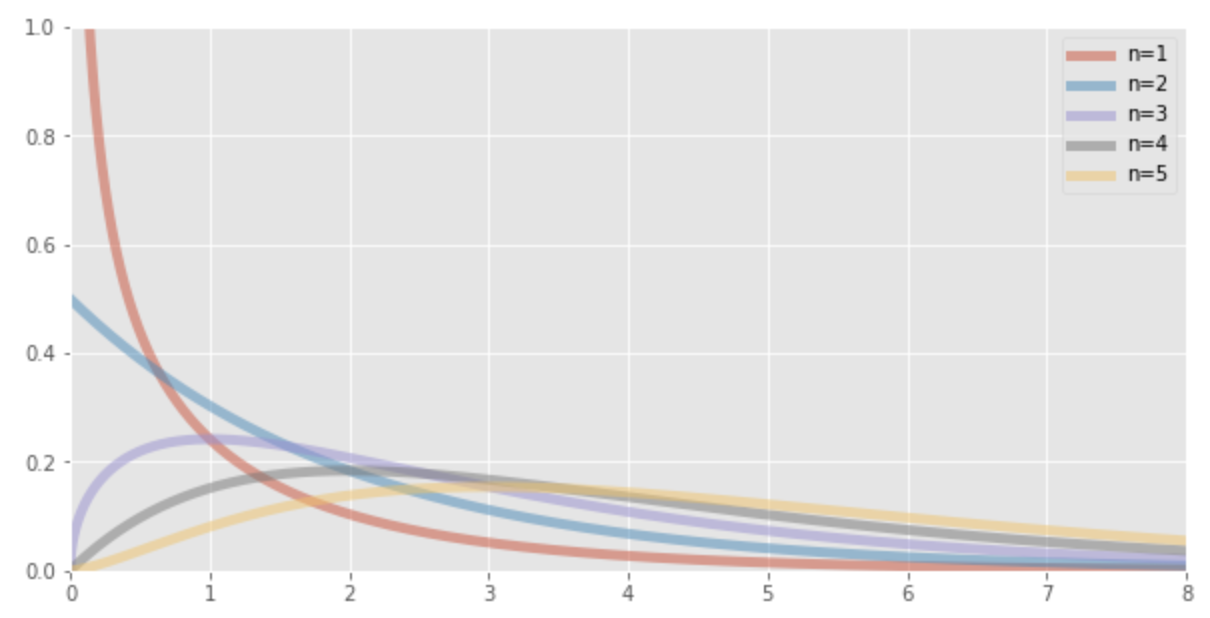
Hubungan dengan distribusi normal standar

Distribusi chi-square dengan 1 derajat kebebasan sama dengan variabel acak kuadrat X_1 mengikuti distribusi normal standar.

Nilai yang diharapkan dan varians dari distribusi chi-square

Nilai yang diharapkan dan varians dari variabel acak X yang mengikuti distribusi F F(m, n) masing-masing adalah:

Tabel distribusi chi-square (sisi atas)

Karena distribusi chi-square hanya memiliki parameter n, probabilitas dari distribusi chi-square dapat dirangkum dalam sebuah tabel yang disebut tabel distribusi chi-square. Di bawah ini adalah tabel distribusi chi-square yang merangkum derajat kebebasan dari distribusi chi-square dengan probabilitas sisi atas \alpha masing-masing sama dengan 0.1, 0.05, 0.025 dan 0.01.

Sebagai contoh, jika Anda ingin mencari titik 5% atas dari distribusi chi-square dengan 5 derajat kebebasan, carilah nilai di persimpangan n = 10 dan \alpha = 0.05. Dengan demikian, titik persentil ke-5 atas yang Anda cari adalah 11.07.

Sifat reproduksi dari distribusi chi-Square

Misalkan variabel acak X dan Y masing-masing mengikuti distribusi chi-square dan saling independen sebagai berikut:

Dalam kasus ini, X + Y mengikuti distribusi chi-square berikut

Sifat ini disebut sifat reproduktif.

Sampel acak dari populasi yang mengikuti distribusi normal dan distribusi chi-square

Dalam sampel yang dipilih secara acak X_1, X_2, \cdots, X_n dari populasi yang mengikuti distribusi normal N(\mu, \sigma^2), dimana setiap X mengikuti distribusi normal secara independen satu sama lain, variabel acak berikut W mengikuti distribusi chi-square dengan n-1 derajat kebebasan.

Juga, karena varians tak bias adalah S^2, W juga dapat dinyatakan sebagai berikut:

Kode Python

Berikut ini adalah kode Python yang digunakan untuk menggambar distribusi chi-square.

from scipy.stats import chi2
import numpy as np
import matplotlib.pyplot as plt

plt.style.use('ggplot')
fig, ax = plt.subplots(facecolor="w", figsize=(10, 5))

x = np.linspace(0, 8, 10000)

k_deg = [1, 2, 3, 4, 5] # degree of freedom

for i in k_deg:
    plt.plot(x, chi2.pdf(x, i), linestyle='-', label='n={}'.format(i), lw=5, alpha=0.5)

plt.xlim(0, 8)
plt.ylim(0, 1)
plt.legend()
plt.show()