What is Covariance

Covariance is a numerical value that represents the relationship between two variables, X and Y. It tells us whether an increase in one variable is associated with an increase or decrease in the other variable.

If the covariance is positive, it indicates that both variables tend to increase or decrease together. If the covariance is negative, it means that as one variable increases, the other tends to decrease, and vice versa. A covariance of zero implies that there is no linear relationship between the variables.

The mathematical representation of the covariance between variables X and Y is given as:

Where:

• cov(X,Y): Covariance between variables X and Y
• X_i and Y_i: Individual data points for variables X and Y
• \overline{X} and \overline{Y}: Mean of variables X and Y
• n: Number of data points

Covariance vs. Correlation

While covariance measures the direction of the relationship between two variables, correlation quantifies the strength and direction of that relationship. Correlation is a standardized form of covariance, ranging between -1 and 1, whereas covariance can take any value.

The correlation coefficient, denoted by r, is calculated as:

Where:

• r: Correlation coefficient
• cov(X,Y): Covariance between variables X and Y
• \sigma_X and \sigma_Y: Standard deviations of variables X and Y

Calculating Covariance with Python

In this chapter, I will demonstrate how to calculate covariance using Python, including both positive and negative covariance cases. We will also create plots to visualize the relationships between variables.

First, let's import the necessary libraries.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

Next, we will create a function to calculate the covariance between two variables.

def covariance(x, y):
    x_mean = np.mean(x)
    y_mean = np.mean(y)
    n = len(x)
    cov = np.sum((x - x_mean) * (y - y_mean)) / (n - 1)
    return cov

Let's create an example with positive covariance.

# Generate sample data with positive covariance
np.random.seed(42)
x_positive = np.random.rand(50)
y_positive = x_positive * 3 + np.random.rand(50)

# Calculate the covariance
positive_cov = covariance(x_positive, y_positive)
print(f"Positive Covariance: {positive_cov}")

# Plot the data
plt.figure(figsize=(10, 6))
sns.set(style="whitegrid")
sns.scatterplot(x=x_positive, y=y_positive, s=100, color="blue", edgecolor="black")
plt.title("Positive Covariance Example", fontsize=20)
plt.xlabel("X", fontsize=16)
plt.ylabel("Y", fontsize=16)
plt.show()

Positive Covariance: 0.25587483932859534

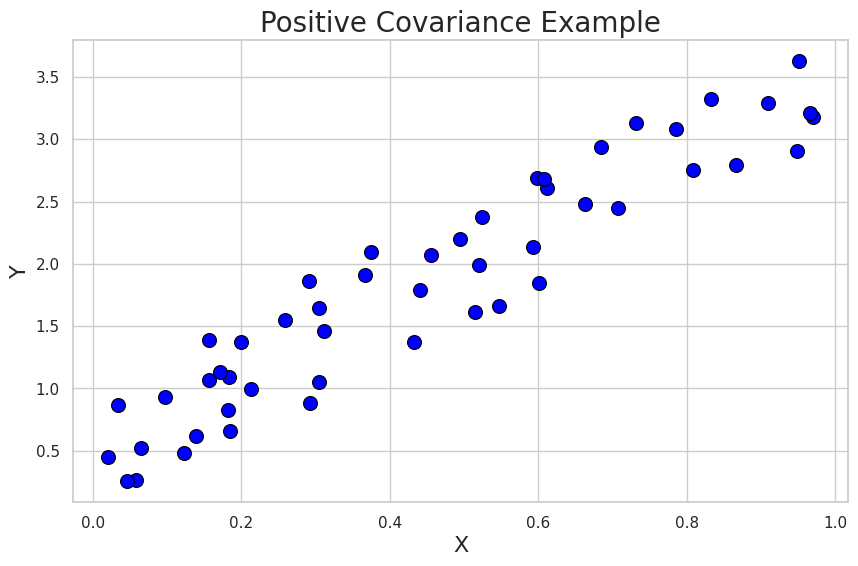
In this example, we can see that as the values of X increase, the values of Y also tend to increase. The plot shows a positive covariance between the variables.

Now, let's create an example with negative covariance.

# Generate sample data with negative covariance
np.random.seed(42)
x_negative = np.random.rand(50)
y_negative = -x_negative * 3 + np.random.rand(50)

# Calculate the covariance
negative_cov = covariance(x_negative, y_negative)
print(f"Negative Covariance: {negative_cov}")

# Plot the data
plt.figure(figsize=(10, 6))
sns.set(style="whitegrid")
sns.scatterplot(x=x_negative, y=y_negative, s=100, color="red", edgecolor="black")
plt.title("Negative Covariance Example", fontsize=20)
plt.xlabel("X", fontsize=16)
plt.ylabel("Y", fontsize=16)
plt.show()

Negative Covariance: -0.2448461835209279

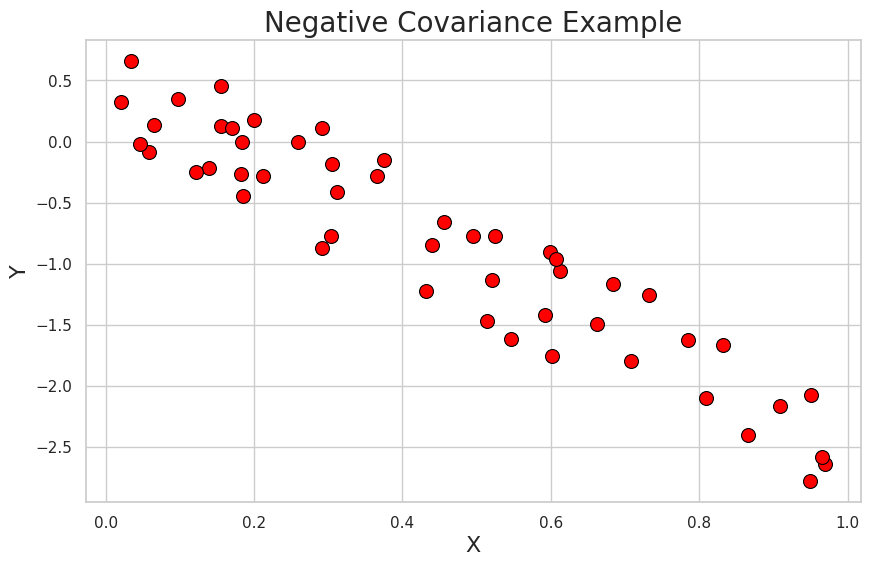
In this example, we can see that as the values of X increase, the values of Y tend to decrease. The plot shows a negative covariance between the variables.