2023-02-03

Principal Component Analysis (PCA)

Apa itu PCA

Principal Component Analysis (PCA) adalah teknik yang banyak digunakan dalam ilmu data, khususnya untuk reduksi dimensi, visualisasi data, dan pengurangan noise. Metode yang kuat ini memungkinkan para peneliti dan praktisi untuk menganalisis dan menemukan pola-pola tersembunyi dalam dataset yang besar dan kompleks, yang dapat memberikan wawasan yang berharga dan meningkatkan pengambilan keputusan.

Essensi dari PCA

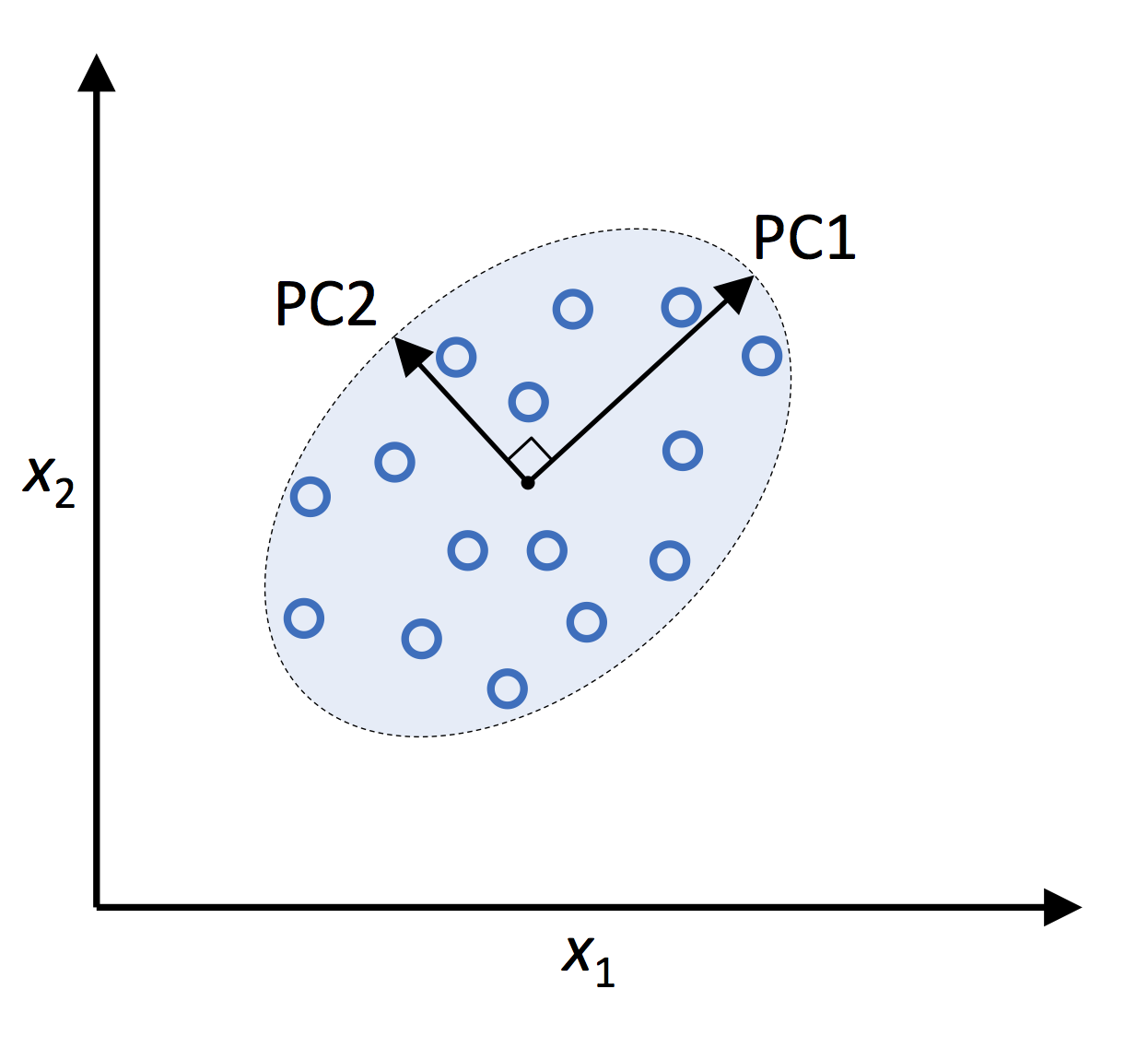
Tujuan utama dari PCA adalah untuk mengurangi dimensi dataset sambil mempertahankan sebanyak mungkin informasi. Hal ini dicapai dengan mentransformasikan fitur-fitur asli menjadi seperangkat fitur yang ortogonal, yang disebut komponen utama (principal components, PC), yang merupakan kombinasi linear dari variabel-variabel asli. Komponen-komponen utama ini diurutkan berdasarkan variansinya, dengan komponen utama pertama yang mampu menjelaskan variansi data terbesar, diikuti oleh komponen kedua, dan seterusnya. Dengan mempertahankan hanya beberapa PC, seseorang dapat secara efektif mengurangi dimensi dataset dan menyederhanakan analisis tanpa kehilangan informasi yang signifikan.

Principal Components
Python Machine Learning (2nd Ed.) Code Repository

Matematika PCA

Pada bab ini, saya akan membahas dasar-dasar matematika dari PCA. Untuk memahami konsep dan teknik yang mendasar, pengetahuan dasar tentang aljabar linear dan statistik sangat diperlukan.

Aljabar Linear dan Nilai Eigen

PCA bergantung pada konsep aljabar linear, khususnya nilai eigen dan vektor eigen. Diberikan sebuah matriks persegi A, sebuah vektor eigen v adalah vektor bukan nol yang memenuhi persamaan berikut:

Av = \lambda v

di mana $\lambda$ adalah nilai eigen yang terkait dengan vektor eigen $v$ . Dalam konteks PCA, nilai eigen dan vektor eigen memainkan peran penting dalam mentransformasikan dataset asli menjadi seperangkat variabel tidak berkorelasi (komponen utama).

Matriks Kovarians

Matriks kovarians adalah elemen kunci dalam PCA, karena matriks ini merepresentasikan hubungan antara variabel asli dalam dataset. Untuk dataset $X$ dengan $n$ sampel dan $p$ fitur, matriks kovarians $C$ adalah matriks simetris $p$ x $p$ , dengan setiap elemen $c_ij$ merepresentasikan kovarians antara fitur $i$ dan fitur $j$ :

C_{ij} = \frac{1}{n-1} \sum_{k=1}^{n}(x_{ki} - \bar{x}i)(x{kj} - \bar{x}_j)

di mana $x_{ki}$ adalah nilai fitur $i$ untuk sampel $k$ , dan $\bar{x}_j$ adalah nilai rata-rata fitur $i$ di seluruh sampel.

Dekomposisi Nilai Eigen

Dekomposisi nilai eigen adalah proses mendekomposisi suatu matriks menjadi nilai-nilai eigen dan vektor-vektor eigenya. Dalam PCA, kita melakukan dekomposisi nilai eigen pada matriks kovarians $C$ , yang menghasilkan satu set nilai eigen dan vektor eigen terkait. Vektor eigen yang terkait dengan nilai eigen terbesar merepresentasikan arah di mana data memiliki variansi tertinggi, dan oleh karena itu menjadi dasar untuk komponen-komponen utama.

Reduksi Dimensi

Setelah kita memiliki nilai eigen dan vektor eigen dari matriks kovarians, kita dapat mengurangi dimensi dataset dengan memilih $k$ vektor eigen teratas yang terkait dengan $k$ nilai eigen terbesar. Vektor eigen ini, juga dikenal sebagai komponen utama, kemudian digunakan untuk mentransformasikan dataset asli $X$ menjadi dataset baru $Y$ dengan dimensi yang lebih rendah:

Y = XW_k

di mana $W_k$ adalah matriks $p$ x $k$ yang berisi $k$ vektor eigen teratas sebagai kolom-kolomnya. Dataset baru $Y$ sekarang memiliki $k$ fitur, yang merupakan kombinasi linear dari $p$ fitur asli dan merepresentasikan arah variansi maksimum dalam data. Dengan mempertahankan hanya sebagian komponen utama, kita dapat secara efektif mengurangi dimensi dataset sambil mempertahankan sebagian besar informasi asli.

PCA dalam Praktik

Pada bab ini, saya akan menjelajahi panduan langkah demi langkah untuk melakukan PCA menggunakan dataset yang tersedia secara publik - yaitu dataset Iris yang terkenal. Dataset ini berisi 150 sampel bunga iris, dengan empat fitur: panjang kelopak, lebar kelopak, panjang mahkota, dan lebar mahkota. Tujuannya adalah untuk mengurangi dimensi dataset sambil mempertahankan strukturnya.

Pra-pemrosesan Data

Sebelum melakukan PCA, sangat penting untuk memproses data. Dua tahap pra-pemrosesan utama adalah standardisasi dan penyesuaian pusat. Standarisasi memperkecil skala fitur sehingga memiliki nilai rata-rata 0 dan standar deviasi 1, sedangkan penyesuaian pusat memastikan bahwa nilai rata-rata setiap fitur adalah 0. Kedua tahap ini diperlukan agar PCA dapat bekerja secara efektif.

Berikut cara memproses dataset Iris menggunakan Python dan library scikit-learn:

python

import numpy as np
import pandas as pd
from sklearn import datasets
from sklearn.preprocessing import StandardScaler

# Load the Iris dataset
iris = datasets.load_iris()
X = iris.data

# Standardize and center the data
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

Melakukan PCA

Sekarang data sudah diproses, kita dapat melakukan PCA menggunakan library scikit-learn. Berikut kode untuk mengurangi dimensi dataset Iris menjadi dua dimensi:

python

from sklearn.decomposition import PCA

# Perform PCA with 2 components
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)

Interpretasi Hasil PCA

Output dari PCA adalah dataset baru (X_pca) dengan dimensi yang lebih rendah. Pada contoh kita, kita mengurangi dataset Iris dari empat dimensi menjadi dua dimensi. Untuk memahami pentingnya setiap komponen utama, kita dapat mengevaluasi rasio variansi yang dijelaskan, yang menunjukkan proporsi variansi total dalam data yang dijelaskan oleh setiap komponen:

python

explained_variance_ratio = pca.explained_variance_ratio_
print(explained_variance_ratio)

Output-nya mungkin seperti ini:

array([0.72962445, 0.22850762])

Ini menunjukkan bahwa komponen utama pertama menjelaskan sekitar 72,96% variansi total dalam data, sedangkan komponen utama kedua menjelaskan sekitar 22,85%. Bersama-sama, kedua komponen ini mewakili sekitar 95,81% dari variansi total.

Visualisasi Komponen PCA

Terakhir, kita dapat memvisualisasikan data yang telah diubah oleh PCA dalam diagram pencar. Ini akan memungkinkan kita untuk mengamati pola atau kluster dalam dataset dengan dimensi yang lebih rendah. Berikut kode untuk membuat diagram pencar dari dua komponen utama menggunakan matplotlib:

python

import matplotlib.pyplot as plt

# Plot the PCA-transformed data
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=iris.target, cmap='viridis', edgecolor='k', s=75)
plt.xlabel('First Principal Component')
plt.ylabel('Second Principal Component')
plt.title('PCA with 2 Components on Iris Dataset')
plt.show()

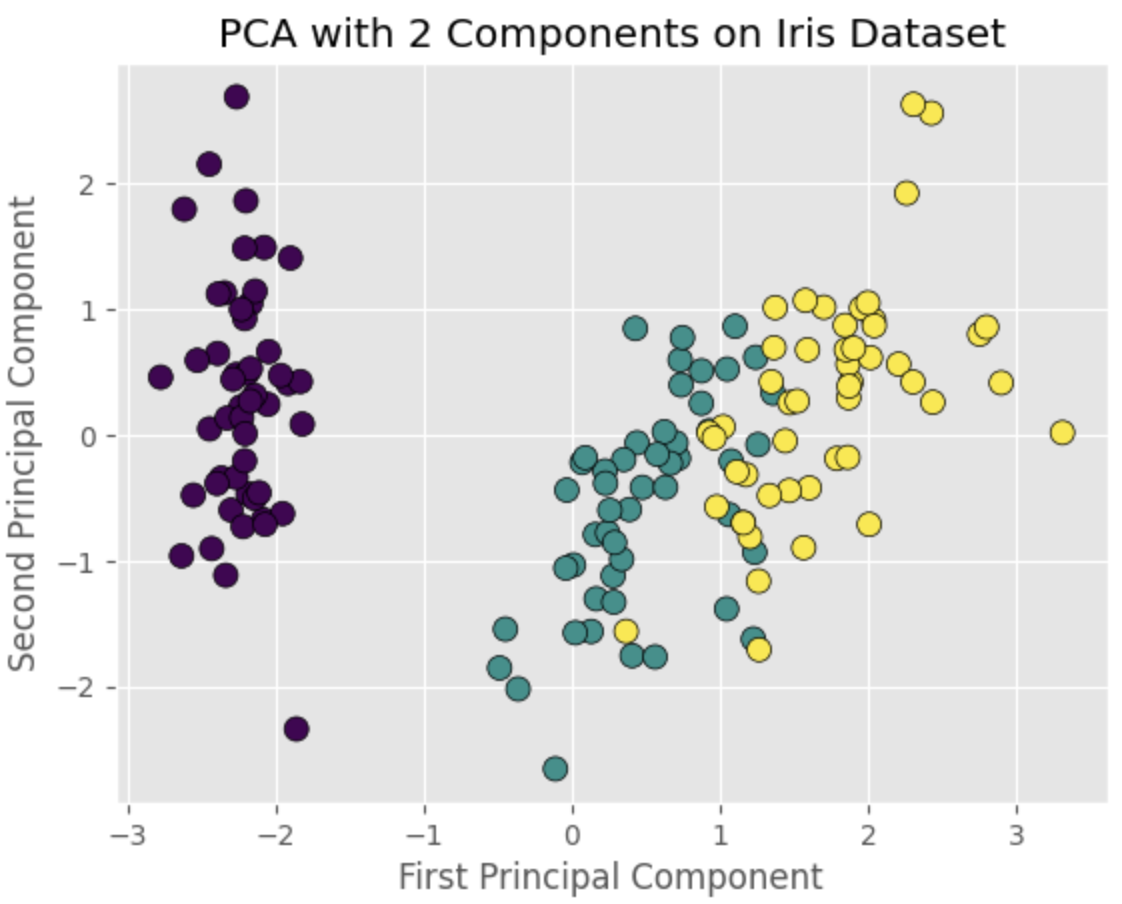
PCA with 2 Components on Iris Dataset

Diagram pencar akan menunjukkan kluster yang berbeda yang sesuai dengan tiga spesies iris, menunjukkan bahwa PCA dapat secara efektif mengurangi dimensi data sambil mempertahankan strukturnya.

Pemuatan Komponen Utama

Pemuatan komponen utama, juga dikenal sebagai pemuatan komponen atau pemuatan vektor eigen, adalah koefisien yang menunjukkan bagaimana setiap fitur asli berkontribusi pada komponen utama tertentu. Menganalisis pemuatan dapat membantu kita memahami hubungan antara fitur asli dan komponen utama, serta struktur data yang mendasarinya.

Berikut cara mendapatkan pemuatan komponen utama untuk dataset Iris menggunakan model PCA yang telah kita implementasikan sebelumnya:

python

loadings = pca.components_
print(loadings)

Output-nya mungkin seperti ini:

array([[ 0.52106591, -0.26934744,  0.5804131 ,  0.56485654],
       [ 0.37741762,  0.92329566,  0.02449161,  0.06694199]])

Array ini mewakili pemuatan untuk dua komponen utama, dengan setiap baris sesuai dengan satu komponen utama dan setiap kolom sesuai dengan satu fitur asli. Semakin besar nilai absolut dari pemuatan, semakin besar kontribusi fitur asli yang sesuai pada komponen utama.

Misalnya, pada komponen utama pertama, panjang mahkota (0,580) dan lebar mahkota (0,565) memiliki pemuatan yang lebih tinggi dibandingkan dengan panjang kelopak (0,521) dan lebar kelopak (-0,269). Ini menunjukkan bahwa komponen utama pertama sebagian besar didorong oleh variasi panjang dan lebar mahkota.

Untuk memvisualisasikan pemuatan, kita dapat membuat biplot, yang merupakan diagram pencar dari data yang telah diubah oleh PCA yang dilapisi dengan vektor yang mewakili pemuatan:

python

def biplot(X_pca, loadings, labels=None):
    plt.figure(figsize=(10, 7))
    plt.scatter(X_pca[:, 0], X_pca[:, 1], c=iris.target, cmap='viridis', edgecolor='k', s=75)

    if labels is None:
        labels = np.arange(loadings.shape[1])

    for i, label in enumerate(labels):
        plt.arrow(0, 0, loadings[0, i], loadings[1, i], color='r', alpha=0.8, lw=2)
        plt.text(loadings[0, i] * 1.15, loadings[1, i] * 1.15, label, color='r', ha='center', va='center', fontsize=12)

    plt.xlabel('First Principal Component')
    plt.ylabel('Second Principal Component')
    plt.title('PCA Biplot of Iris Dataset')
    plt.grid()
    plt.show()

feature_labels = iris.feature_names
biplot(X_pca, loadings, labels=feature_labels)

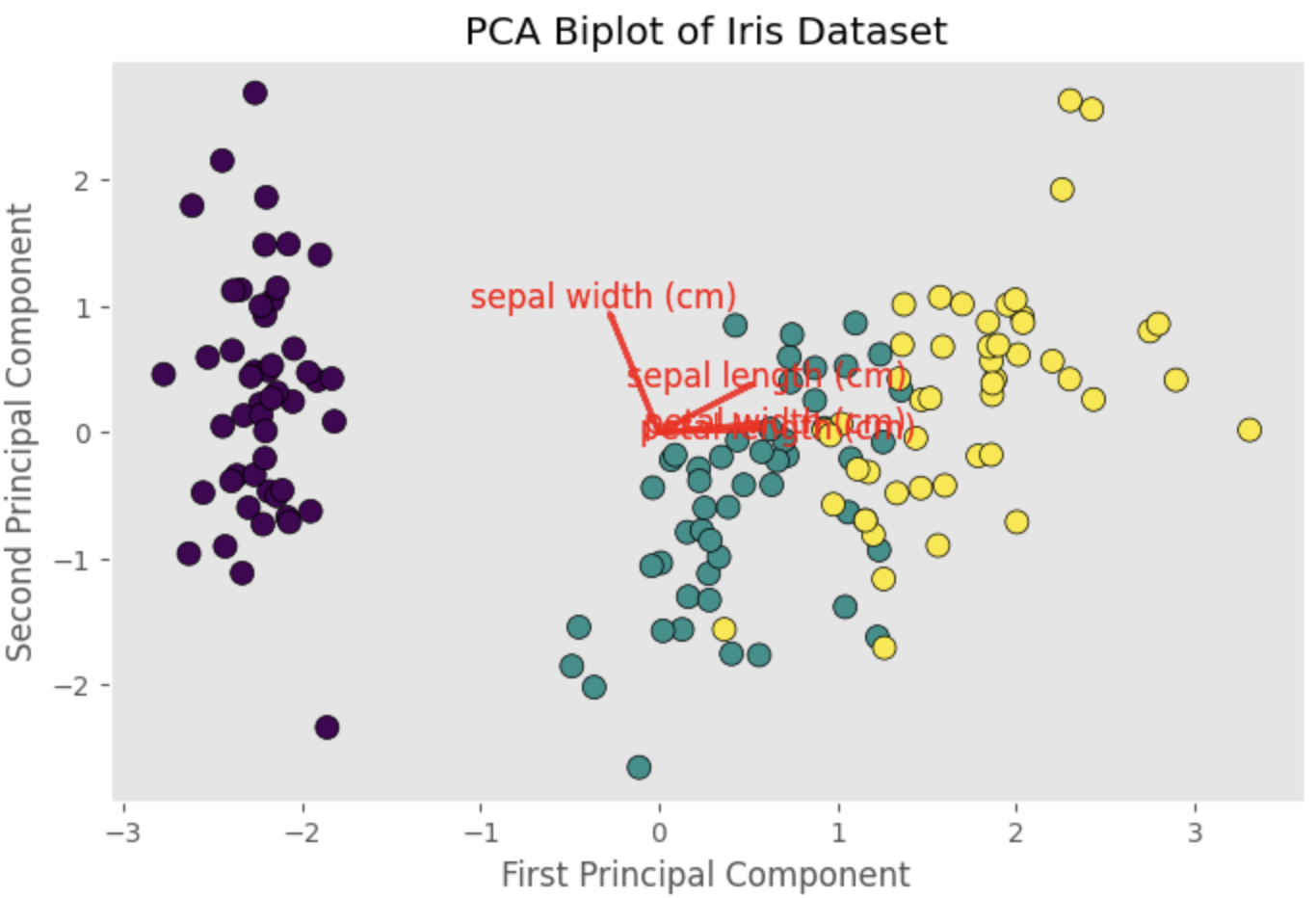
PCA Biplot of Iris Dataset

Biplot akan menampilkan vektor yang mewakili pemuatan untuk panjang kelopak, lebar kelopak, panjang mahkota, dan lebar mahkota. Arah dan panjang setiap vektor menunjukkan kontribusi fitur yang sesuai pada komponen utama. Dengan memeriksa biplot, kita dapat memperoleh wawasan tentang hubungan antara fitur asli dan komponen utama, serta struktur data.